一种加权解卷积波束锐化算法

胡 鑫, 吴雪微, 张 衡, 王文晴, 张 洁

(上海无线电设备研究所,上海201109)

0 引言

实孔径成像技术是利用实孔径雷达探测目标区域的散射中心分布,来对目标区域进行微波成像的[1]。其利用天线波束扫描进行成像,可以弥补合成孔径成像雷达单天线时难以进行前视成像的缺陷[2]。但实孔径成像雷达的成像方位分辨率受天线波束的限制,无法分辨波束宽度内的目标,很难得到高分辨率的成像结果。而波束锐化技术[3]可以在不改变系统的前提下,通过信号处理的方式改善成像效果,使其可以得到固有系统极限外的高分辨率图像。

传统的解卷积波束锐化技术为单通道解卷积算法,这种解卷积算法由于成像系统具有低通特性,因此求解不稳定。多通道解卷积波束锐化算法[4]通常通过单脉冲雷达的和差波束形成多通道,进行波束锐化,具有运算量小,实现简单的优点。然而现有的解卷积波束锐化算法并没有考虑不同接收通道的通道特性差异,算法会引入更大的噪声。本文提出的加权多通道解卷积算法考虑了不同接收通道间的通道特性差异,通过加权使算法引入的噪声更小。

1 算法介绍

1.1 解卷积算法介绍

实孔径成像雷达的回波信号表现为目标散射中心分布函数与天线波束方向图函数的卷积,表达式为

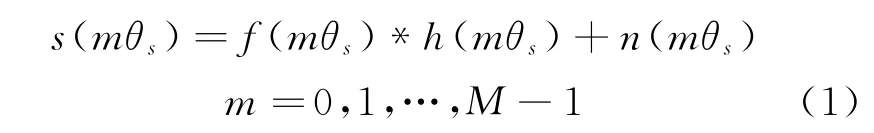
式中:mθs为角度采样序列;θs为角度采样间隔;s(mθs)为实孔径雷达方位向回波信号序列;f(mθs)为目标散射中心分布函数的角度采样序列;h(mθs)为天线波束方向图函数的角度采样序列;n(mθs)为加性噪声序列;M为序列点数。

将式(1)中θs归一化后得到

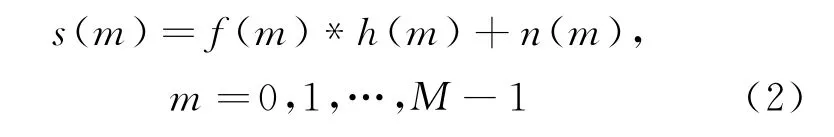
对式(2)进行离散傅里叶变换,有

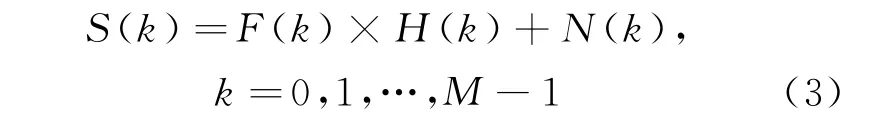
式中:S(k)、F(k)、H(k)和N(k)分别为s(m)、f(m)、h(m)、n(m)的离散傅里叶变换。

由式(3)可得

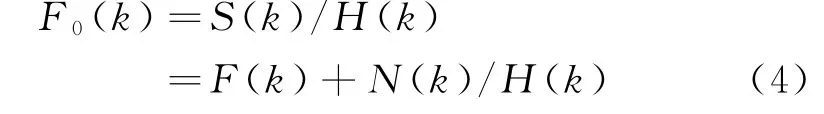
式中:F0(k)为解卷积解的离散傅里叶变换。

对F0(k)进行离散逆傅里叶变换,得到解卷积的解

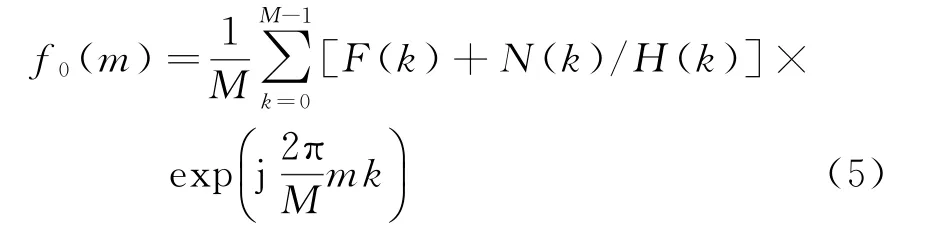
天线的波束方向图函数是一个低通函数,输入信号的高频成分会受到抑制甚至丢失,解卷积波束锐化希望恢复目标散射中心分布函数的高频成分。然而在高频部分1/H(k)很大,N(k)的微弱变化都将导致F(k)的很大变动,使得对目标散射中心分布函数f(m)的估计不连续依赖于观测数据,这就是单通道解卷积方法的病态性。

当系统存在多个通道时,可以通过合理设计多通道解卷积算子,把病态问题转换为良态,得到稳定的解。

通常情况下,天线和差波束方向图函数不同时为0。为解决单通道解卷积方法的病态性,可以引入和差双通道来进行多通道解卷积。和差通道的回波信号表达式为

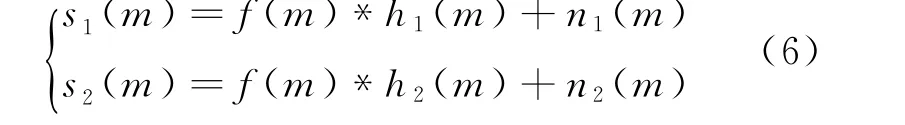
式中:s1(m)为实孔径雷达和波束接收信号;h1(m)为天线和波束方向图函数;n1(m)为和通道噪声;s2(m)为实孔径雷达差波束接收信号;h2(m)为天线差波束方向图函数;n2(m)为差通道噪声。

对式(6)进行傅里叶变换,有

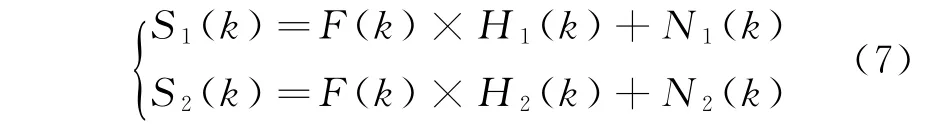
由式(7)可得

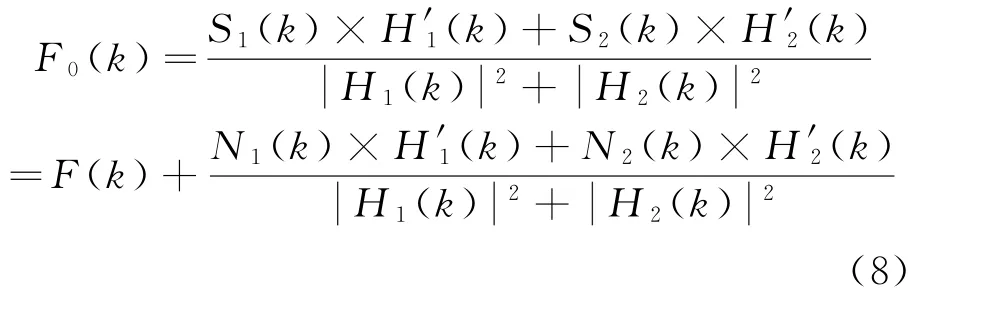
式中:H′1(k)、H′2(k)分别为H1(k)、H2(k)的共轭。

多通道解卷积的解f0(m)为F0(k)的离散逆傅里叶变换。

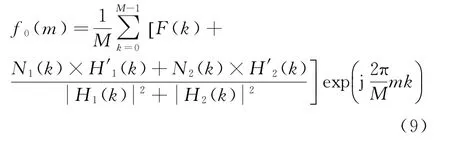
多通道解卷积算法,不更改工程系统的组成,仅在成像算法上进行改进,方法简单可控,工程实现简单。

1.2 加权解卷积算法

在同一系统中,不同的接收通道一般存在通道特性的差异,传统的多通道解卷积算法并没有考虑和差接收通道的通道特性差异。和差接收通道存在通道特性差异时,两个通道的增益和噪声会不一致。系统接收信号可以表示为

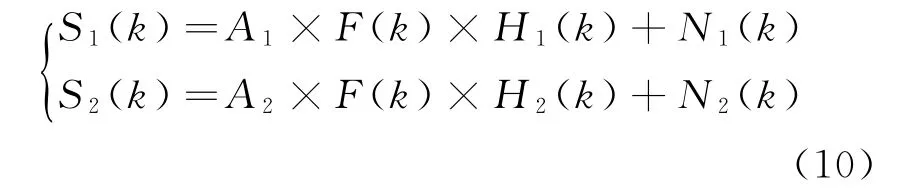
式中:A1和A2分别为两个通道的增益,在A1和A2不相等时,式(9)的公式并不适用。这时需要对和差通道的接收信号进行归一化。即

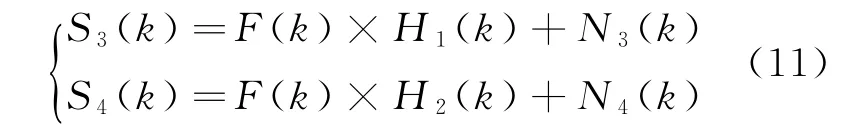
式中:S3(k)=S1(k)/A1;S4(k)=S2(k)/A2;N3(k)=N1(k)/A1;N4(k)=N2(k)/A2。N3(k)和N4(k)均为加性白噪声,但其平均功率通常并不相同。

由式(11)算术变换得到

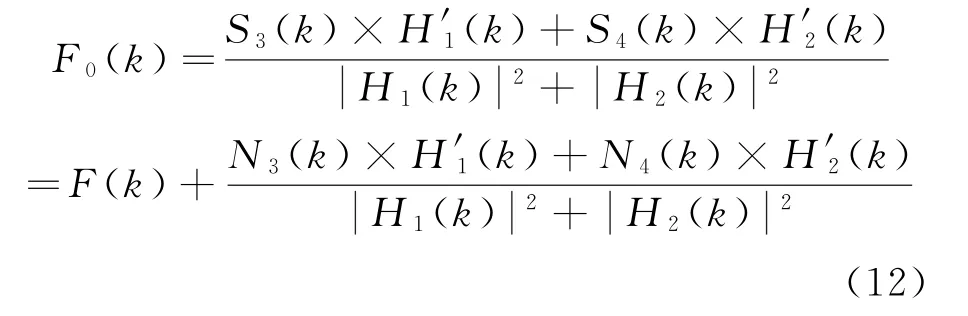
为减少算法引入的噪声,对式(12)进行加权处理,设加权系数为w,得到

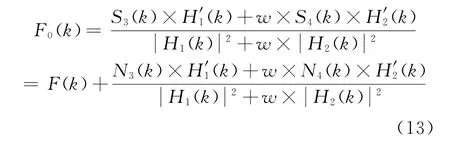
引入的平均噪声功率为

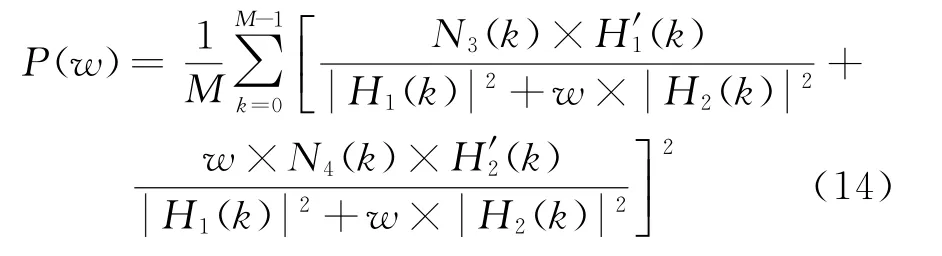
因N3和N4为相互独立的高斯白噪声,可知P(w)=

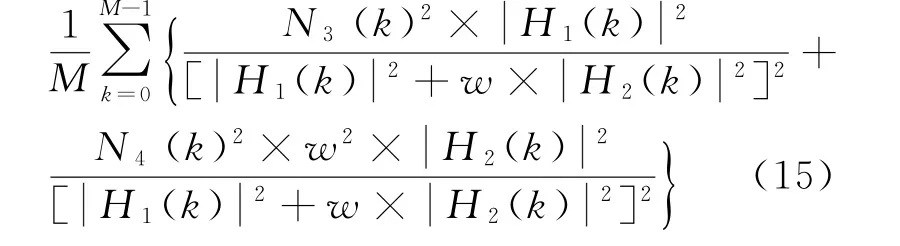
为使噪声功率最小,对式(15)求导得到

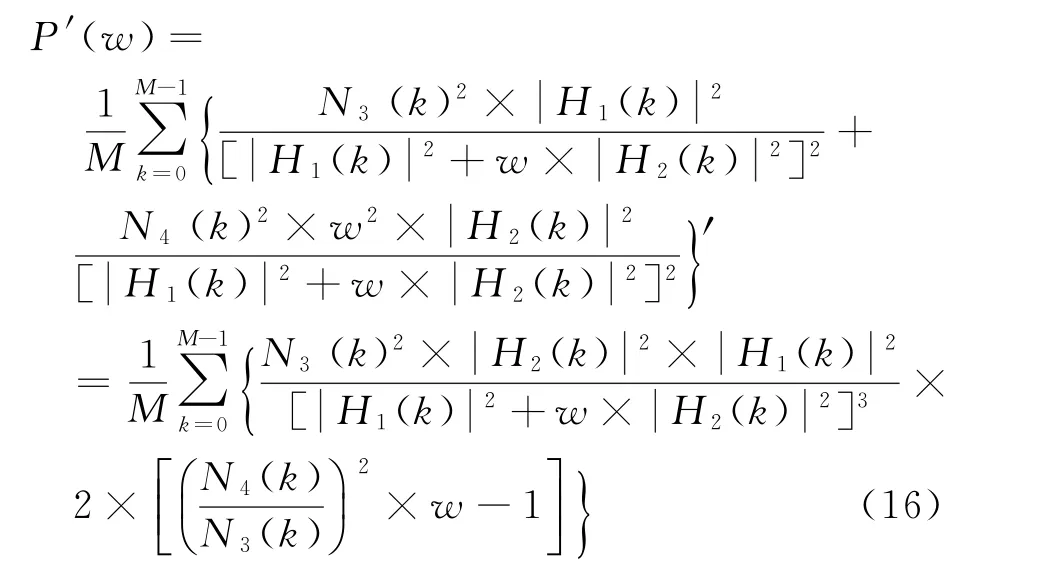
令PN3和PN4分别代表N3和N4的平均噪声功率。显然,w=(N3/N4)2=PN3/PN4时,P′(w)=0;w＜(N3/N4)2=PN3/PN4时,P′(w)＜0;w＞(N3/N4)2=PN3/PN4时,P′(w)＞0。当加权系数w=PN3/PN4时,P(w)存在最小值,即算法引入的噪声功率最低。

2 算法仿真

为了验证加权解卷积波束锐化方法的性能,进行了matlab仿真:先设置目标参数,然后根据天线波束方向图,计算和差通道回波;计算加权系数,进行噪声加权解卷积,最后输出结果。

选取方位角-4.83°～+4.83°范围的区域进行波束锐化算法的仿真,选用的天线和差波束方向图如图1所示。角度采样间隔为0.01°(共计967点),其中和波束方向图为h1(m),差波束方向图为h2(m)。归一化目标散射中心分布f(m)为5个点幅度不为0,位置-幅度坐标分别为(-0.04°,0.71),(-0.02°,0.5),(0°,1),(0.02°,0.71),(0.04°,0.5),其余点幅度为0,如图2所示。

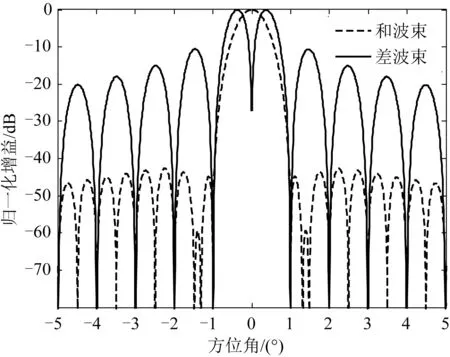
图1 天线和差波束方向图

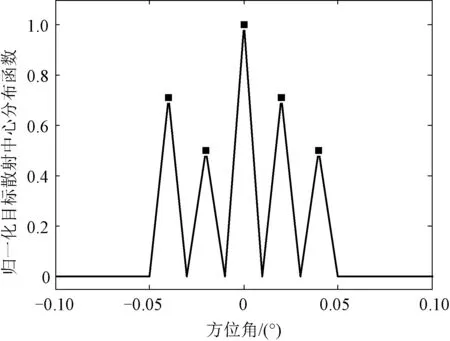
图2 目标散射中心分布

图3为无噪声情况下的波束锐化结果,图像与目标散射中心分布完全一致。

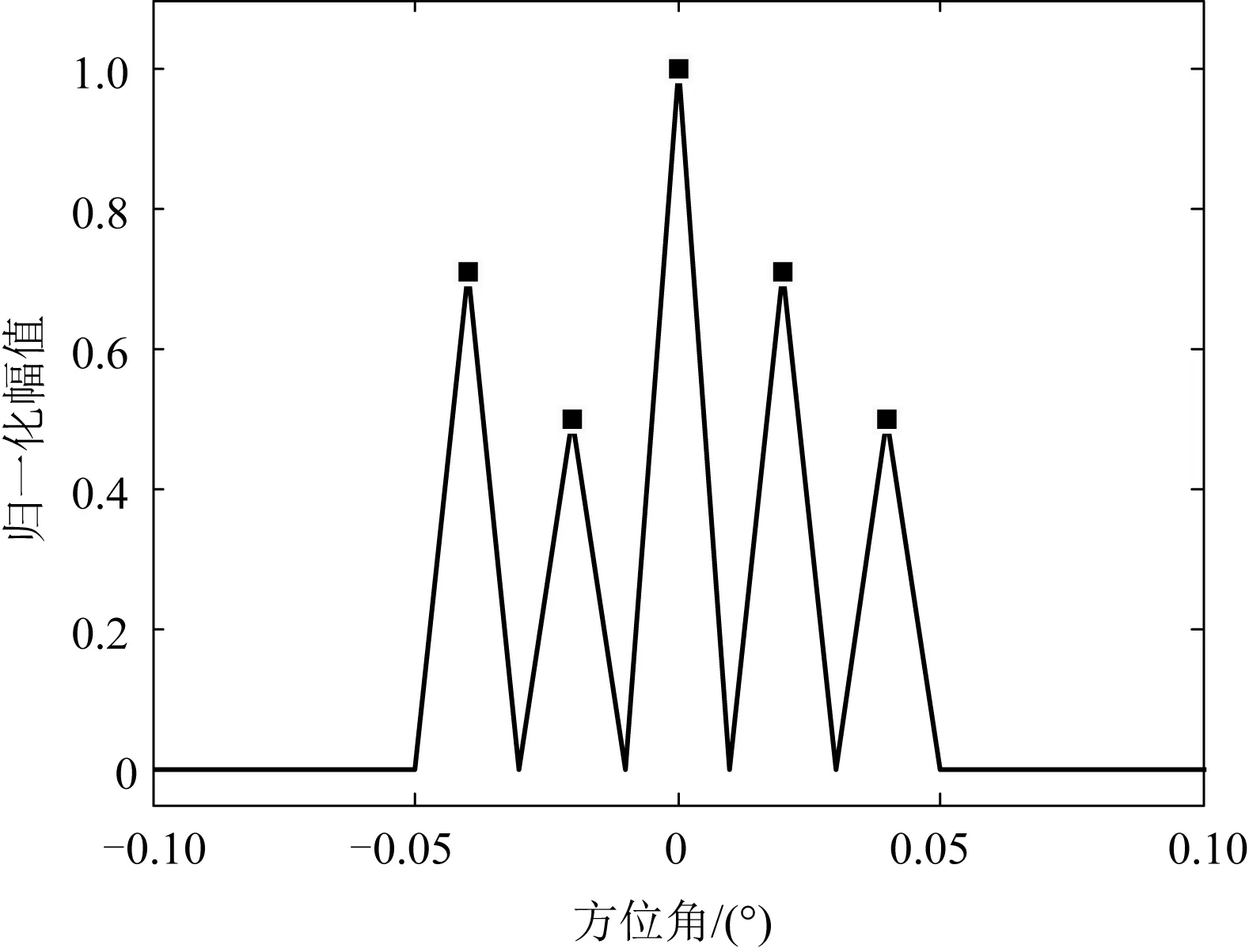
图3 无噪声情况下的波束锐化结果

设和通道归一化平均噪声功率为-57.25dB,差通道归一化平均噪声功率为-51.25dB,进行仿真分析。

图4为该条件下微波图像的不加权波束锐化结果。用式(17)对波束锐化结果进行平均噪声功率估计可知,归一化平均噪声功率约为-14.46dB。

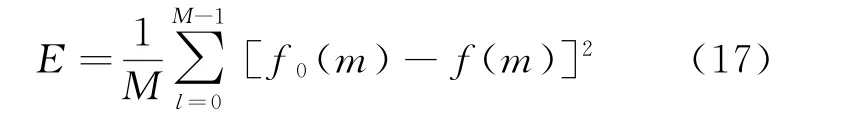
图4 仿真条件下波束锐化结果

算法引入的噪声可以用进行解卷积运算前后信号归一化平均噪声功率的增加值来表示。图5为该条件下根据式(14)计算得到的不同加权系数下算法引入的噪声理论曲线。图6为相同条件下,采用加权波束锐化算法,不同加权系数下,算法引入噪声的仿真结果。波束锐化算法引入噪声的仿真结果与理论值一致(为避免偶然性,图6为500次仿真结果的平均值)。显然在加权系数为-6 dB时,波束锐化算法输出结果的归一化平均噪声功率最低。

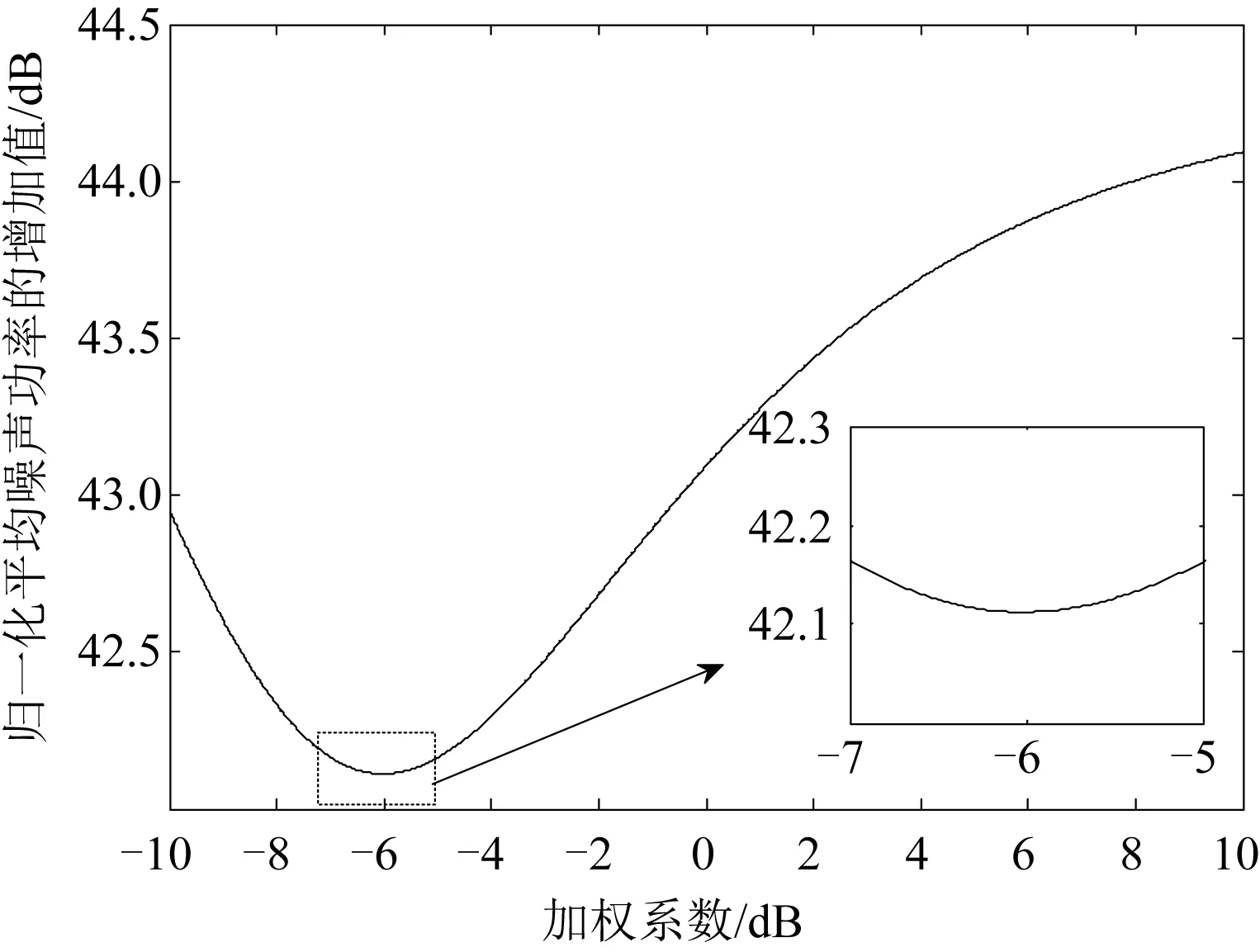
图5 算法引入噪声的理论值

图7为加权系数为-6dB时,微波图像的加权波束锐化结果。用式(17)对加权波束锐化结果进行平均噪声功率估计可知,归一化平均噪声功率约为-15.30dB。显然加权波束锐化算法可以获得归一化平均噪声功率更低的结果。

3 结论

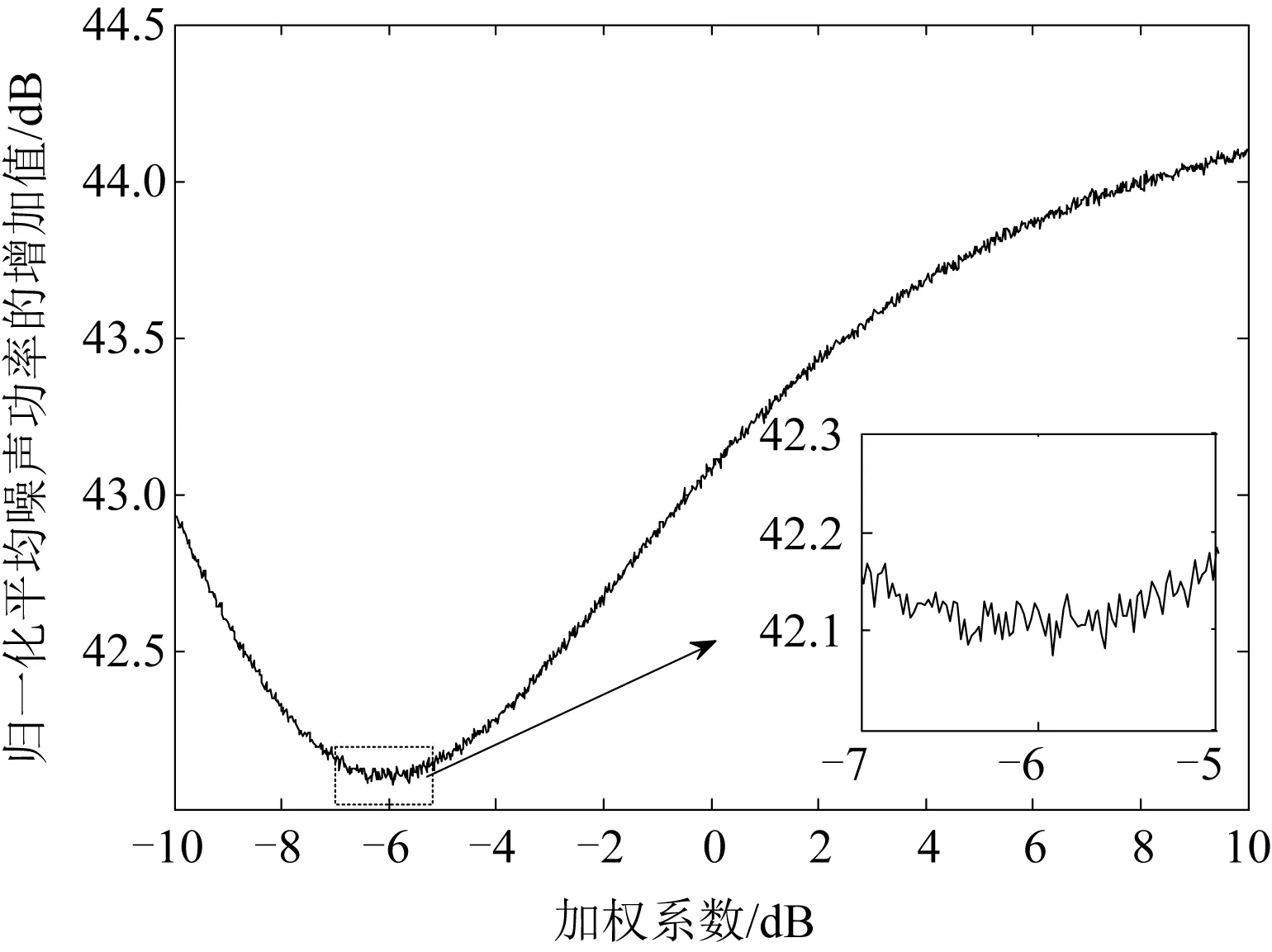
图6 算法引入噪声的仿真结果

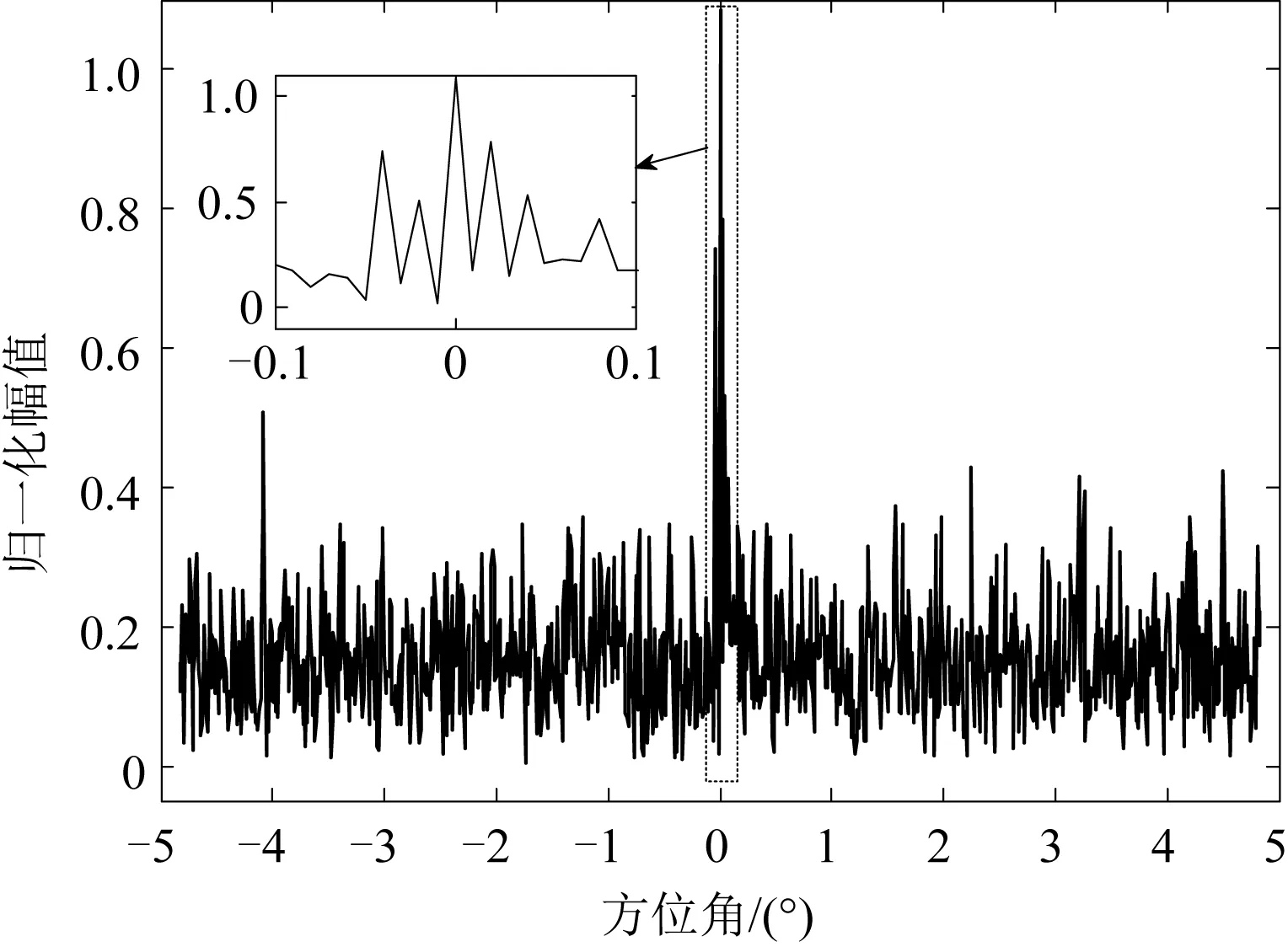
图7 仿真条件下加权波束锐化结果

本文提出了一种加权解卷积波束锐化算法,在不改变硬件的基础上,改善成像结果。并针对通道特性差异导致不同通道接收信号的幅度、噪声不一致的情况,提出了加权解卷积波束锐化算法。该算法可以利用不同通道的归一化平均噪声功率,计算并采用合理的加权系数,使算法引入的噪声最小,从而改善波束锐化结果的信噪比。仿真结果表明,相较于常规多通道解卷积的波束锐化算法,采用加权解卷积算法可以获得信噪比更高的波束锐化结果,具有较好的工程实用性和可实践性。