基于多维压缩感知的雷达成像方法研究

于 欢, 王凤姣, 李乃星, 胡 鑫, 周起华

(上海无线电设备研究所,上海201109)

0 引言

雷达的回波信号包含目标距离、方位和俯仰三个维度的信息。传统的成像雷达获得的目标图像实际上是其三维结构在距离-多普勒平面上的投影。当雷达与目标存在相对运动时,目标在该平面上的投影也会相应发生变化,成像结果反映了目标的一维方位和俯仰信息。而从雷达三维成像结果中可以获取目标三个维度的信息,从而更直观地对目标进行描述。压缩感知理论可以代替匹配滤波实现脉冲压缩,降低雷达系统设计的复杂度。本文建立了一种基于多维压缩感知的雷达成像模型,并针对雷达回波信号稀疏度未知影响信号重构精度的问题,提出了改进的分段正交匹配追踪算法,实现雷达压缩感知三维成像。

1 基于压缩感知的雷达成像模型

1.1 多维压缩感知模型

压缩感知理论[1]基于信号的稀疏性以及线性规划,旨在降低信号的采样频率,重构出高分辨率的信号。压缩感知主要包括信号的稀疏表示、信号的测量以及信号的重构三个部分,如图1所示。

图1 压缩感知理论框架

假设原始信号X是有限长的离散信号,且X∈C C N,在ψ变换域上能够稀疏表示为

式中:ψ是N×N的稀疏矩阵;S是一个N×1的矩阵,满足‖S‖0=K≪N,‖S‖0表示矩阵S中的非零元素个数。将信号X稀疏后,通过非相关测量将信号X投影到维数更低的矩阵φ上去,即

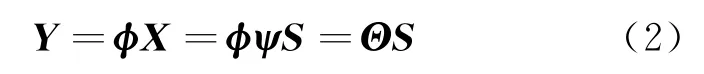
式中:Y是一个M×1(M＜N)的矩阵;φ∈CCM×N,表示测量矩阵;Θ∈CCM×N,表示观测矩阵。式(2)可以转化为最小l0范数问题求解,即

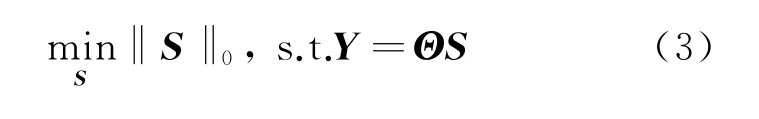
多维压缩感知模型[2]是在二维压缩感知模型[3]以及多维矢量矩阵[4-5]理论的基础上推导得到的。假设多维信号X在ψ变换域上是稀疏的,将多维矩阵XK1×K2×…×Kr的维数分成两组,用矢量I、J表示,其中I=(K1,K2,…,Km),J=(Km+1,Km+2,…,Kr),X表示为多维矢量矩阵XIJ。XIJ在ψ变换域上能够稀疏表示为

式中:ψUI、ψVJ表示多维矢量稀疏矩阵,多维矩阵ψ的维数分别按矢量U、I以及V、J分成两组,其中U=(K1,K2,…,Kn),V=(Kn+1,Kn+2,…,Kr);SUV是稀疏后的矩阵。XIJ经过非相关测量得到测量结果为

式中:YPQ是多维矢量测量值;φPI、φQJ表示多维矢量测量矩阵;多维矩阵φ的维度分别按矢量P、I以及Q、J分成两组,其中P=(K1,K2,…,Kl),Q=(Kl+1,Kl+2,…,Kr)。由多维测量值YPQ实现信号的重构,可总结为下列优化问题,即

根据上述内容可得到三维压缩感知模型。假设存在三维信号X∈CCN×N×N,可表示为三维矢量矩阵。其稀疏变换矩阵分别为,记为ψ1和ψ2。信号测量时测量矩阵分别为,记为φ1和φ2。则重构三维信号X∈CCN×N×N的问题可表示为

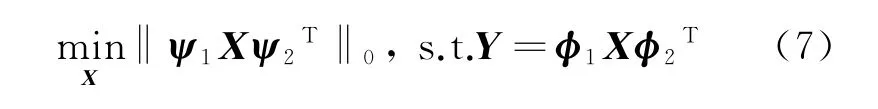
根据矩阵拉直运算可得到Vec(S)以及Vec(Y),进一步可得到

式中:⊗表示两个矩阵之间的Kronecker积。因此,三维压缩感知模型下的优化问题可表示为

最后通过贪婪算法等重构算法得到三维信号。

1.2 雷达成像几何模型

由于多发多收(Multiple Input Multiple Output,MIMO)雷达的收发阵列是面阵,可同时发射并接收多个相互独立且正交的信号,因此MIMO雷达可以获取更多的目标信息。

本文中采用一种收发阵列为面阵的M2发N2收的MIMO雷达[6]。假设收发面阵在xoy平面上,发射阵元及接收阵元的间距分别为dt、dr,满足dt=(M-1)Nd,dr=2d,其中阵元间距为d。稀疏阵面可等效成(MN)2个收发共用阵元的均匀正方形阵列,如图2所示。φ和θ分别表示目标相对于收发阵元的俯仰角和方位角。

图2 基于多维压缩感知的雷达成像系统几何模型

1.3 雷达成像信号模型

第m个发射阵元发射的信号sm可表示为

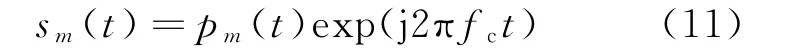
式中:pm(t)是第m个发射阵元发射信号的复包络;fc是载波频率。经K个目标点散射,第n个接收阵元接收到的信号可表示为

式中:K表示目标所划分的网格点总个数;σk表示第k个目标点的散射系数;τn,m(k)表示第m个发射阵元发射,第n个接收阵元接收第k个目标点反射信号的时延。以Q个采样频点对空间频谱均匀采样,接收信号在去载波以及时延处理后可表示为

式中:Gn,m(fq)表示第m个发射阵元发射,第n个接收阵元接收的信号,在第q个频点采样时的空间频谱;fq=Bq/Q,表示第q个采样频点,B为信号的带宽;rk表示坐标原点到第k个目标点的向量,可由该目标点的坐标(xk,yk,zk)表示;分别表示Gn,m(fq)在x、y、z三个维度的单位频谱;φn和θn分别为目标相对于第n个接收阵元的俯仰角和方位角;φm和θm分别为目标相对于第m个发射阵元的俯仰角和方位角。

根据上文所述,可以构造第k个目标点的三维回波信号模型,即

其中

式中:Rk∈CCM2N2Q×1;φk∈CCM2N2Q×1,为测量矩阵;φn,m(k)表示在第m个发射阵元发射第n个接收阵元接收第k个目标点的测量矩阵;e∈CCM2N2Q×1,为加性零均值高斯白噪声。根据式(16)、式(17)可得到

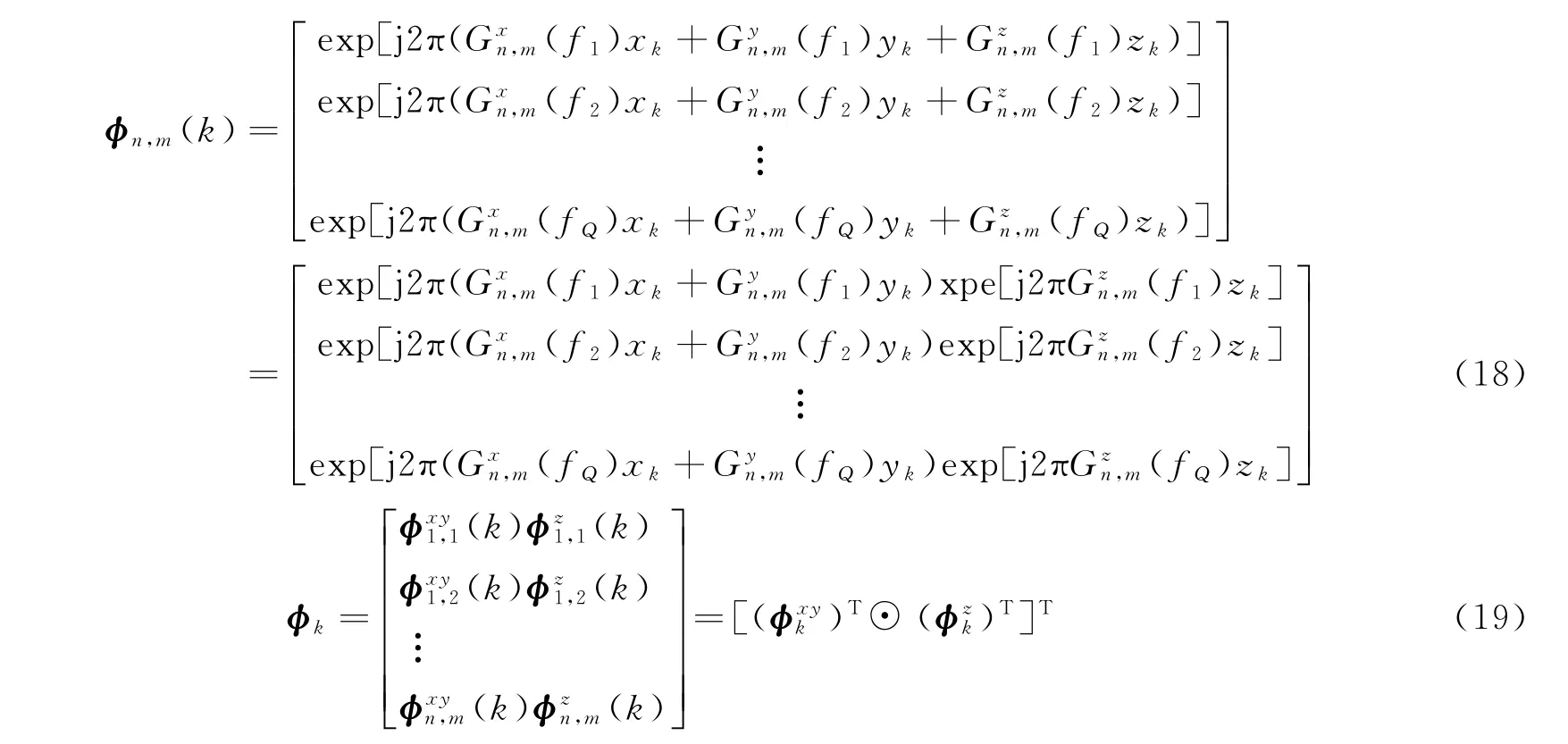
K-R积和Kronecker积可表示为

式中:a=[a1,a2,…,aM2N2Q]和b=[b1,b2,…,bM2N2Q]分别为的行矢量。根据上述两种乘积的性质将第k个目标点的三维信号模型转换为

式中:diag(·)表示由括号内矢量构成的对角矩阵。

2 改进的分段正交匹配追踪算法

分段正交匹配追踪(Stagewise Orthogonal Matching Prusuit,St OMP)算法[7]相较于正交匹配追踪(OMP)算法[8]不再是每次迭代过程中选取一个最佳的原子,而是根据预先设定的阈值范围选取多个原子,从而减少迭代次数。

StOMP算法的步骤[9]如下:

a)输入观测矩阵Θ,测量矩阵φ,稀疏矩阵ψ,观测向量Y,迭代次数t,终止最大迭代次数T,每次迭代索引(列序号)J,t次迭代索引(列序号)集合Λt;

b)初始化,t=1,残差r0=Y,信号支撑集Λ0=∅,J=∅;

c)计算向量内积u(j)=〈rt-1,Θj〉,其中Θj为Θ的第j列,且1≤j≤N;

d)根据阈值,将选取的索引值放到信号支撑集中。令δt为噪声系数,gt为阈值参数,则J={j:u(j)≥δtgt},Λt=Λt-1∪J;

g)t=t+1,如果t＜T则返回步骤(c)继续迭代,直至t=T;

传统的St OMP算法存在以下两个缺点:

a)无法确定重构信号的稀疏度;

b)重构结果依赖于终止条件,错误原子的引入造成重构精度的降低,即在St OMP算法的迭代过程引入错误的索引值(列序号)。

结合稀疏度自适应思想[10],在两种改进的信号稀疏求解算法[11-12]的基础上提出一种针对本文中三维信号模型的改进的St OMP算法。

改进的St OMP算法的步骤如下:

a)输入观测矩阵Θ,测量矩阵φ,稀疏矩阵ψ,观测向量Y,步长l,迭代次数t,迭代阶段tstage;

b)初始化,t=1,残差r0=Y,信号支撑集Λ0=∅,J=∅,l=ls;

c)计算向量内积u(j)=〈rt-1,Θj〉,其中Θj为Θ的第j列,且1≤j≤N,J={j:u(j)≥δtgt};

d)再选取u中l个最大值,设其对应的列序号j的集合为H,Λt=Λt-1∪J∪H;

f)在中选取绝对值最大的l项记为,其对应的列序号集合为F=ΛtL;

h)若‖rt‖2＞‖rt-1‖2时,则停止迭代进入步骤(i);若‖rt‖2＜‖rt-1‖2时,则t=t+1,Λt=F,进入步骤(c);若‖rt‖2=‖rt-1‖2时,则tstage=tstage+1,l=tstage×l,Λt=F,进入步骤(c);

3 仿真结果与分析

为验证改进的St OMP算法对三维雷达信号的重构效果,利用MATLAB进行仿真实验。假设图2雷达成像系统几何模型中,收发天线阵列分布在xoy平面上,中心位置位于空间直角坐标系的坐标原点。雷达发射阵元个数M2=9,接收阵元个数N2=64,发射阵元间距dt=16 m,接收阵元间距dr=2 m,可以等效成收发阵元间距为d=1m的24×24个收发共用阵元的均匀正方形阵列。信号载波频率fc=10 GHz,带宽B=50MHz,采样次数Q=20,对成像区域内的10个目标点进行成像,成像区域大小为10 m×10 m×10 m。重构结果如图3所示。

图3 三维雷达信号目标重构结果

由图3可知,改进的St OMP算法可以将目标点准确地重构出来,并保留目标点的俯仰信息、方位信息以及距离信息。用成像误差,即成像均方根误差(Root Mean Square Error,RMSE),表示成像结果与原目标位置偏离程度,表达式为

本文所提出的改进的St OMP算法与OMP算法、St OMP算法重构效果的对比结果如图4所示。由图4(a)可以看出,相同稀疏度条件下,改进的St OMP算法的信号重构成功概率要高于OMP算法以及St OMP算法;由图4(b)可以看出,同样信噪比条件下,采用改进的St OMP算法的成像误差小于OMP算法以及St OMP算法,成像质量更高。

4 结论

本文推导出一种基于多维压缩感知理论的雷达三维信号模型,并研究得到一种适用于该信号模型的改进的St OMP算法,用于进行信号重构。研究表明:在本文所提出的雷达三维模型基础上,改进的St OMP算法克服重构信号稀疏度未知,以及重构过程中结束条件导致错误原子引入的缺点,提高了信号的重构效果,完整地保留了目标点的俯仰向、方位向以及距离向三个维度的信息。

图4 改进St OMP算法与其他算法重构效果对比图