电子设备热仿真建模方法研究

高林星, 李 前, 陆雪鹏, 周起华

(上海无线电设备研究所,上海201109)

0 引言

近年来,随着电子设备向小型化、集成化的方向发展,电子设备的热流密度快速增长,如何对其进行散热设计已经成为制约电子产品技术发展的重要瓶颈[1-3]。目前计算机仿真已经代替经验设计和试验测试,成为主流的散热设计手段。然而在应用仿真技术时,如何建立准确合理的仿真模型,是阻碍仿真技术顺利实施的问题之一[4]。在进行电子设备热分析时,经常面临着模型复杂度和计算精度的矛盾。详细建模可以带来较为精确的结果,同时会占用较大的计算机资源,耗时、费力。集总参数法、热阻网络法等简化建模方法可以减少计算网格,但在某些场合会带来较大的误差。因此,针对不同层次的热设计,有效地对模型进行简化,是仿真设计的基本要求。

本文针对电子组件热仿真中的模型简化问题,对芯片、电路板及电子单机的等效建模方法进行研究,提出不同方法对应的热设计场合,为电子组件的热设计提供了一定的参考。

1 数值方法原理

1.1 数值传热学

数值传热学采用数值方法来求解描述流动和传热的控制方程。其求解问题的基本思路:将在时间和空间坐标中连续的物理场,用有限个离散点的值所组成的集合来代替;建立这些值的代数关系式,即离散方程;通过求解离散方程来求得离散点的值。数值传热学中常用的数值方法为有限差分法、有限元法和有限体积法。目前主流的电子组件热仿真软件都是基于有限体积法,本文重点介绍有限体积法的基本原理。

1.2 有限体积法

有限体积法是基于三大守恒定律建立控制方程[5],其控制方程可以表达为连续性方程、动量方程和能量方程。

连续性方程为

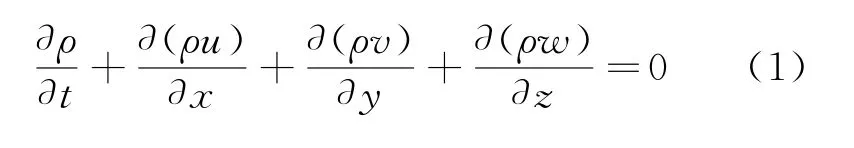
动量方程为

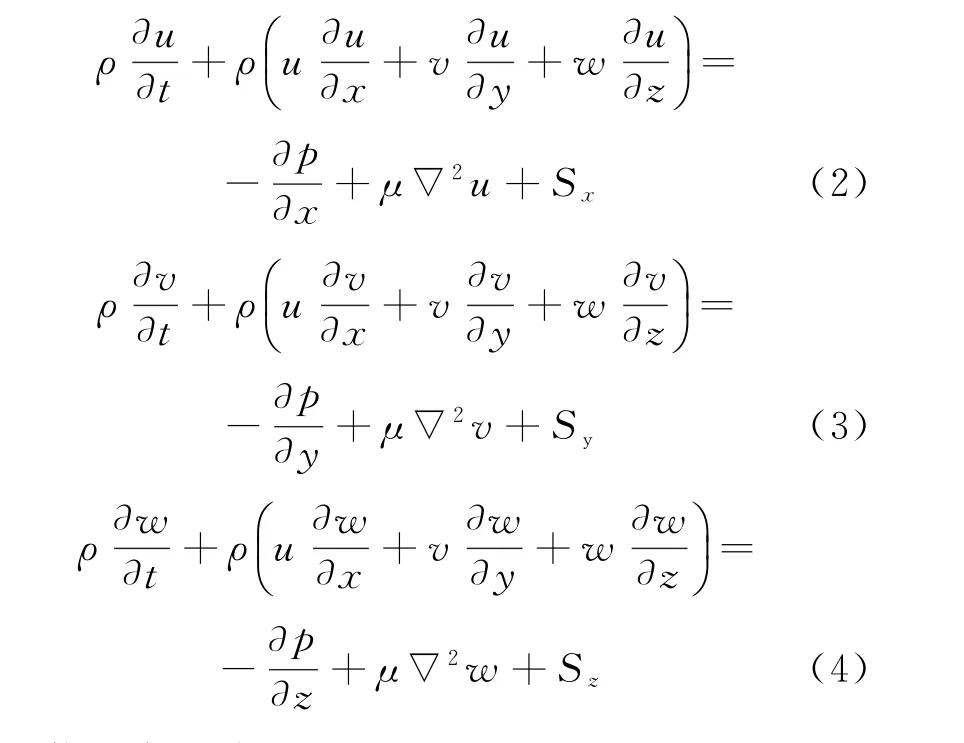
能量方程为

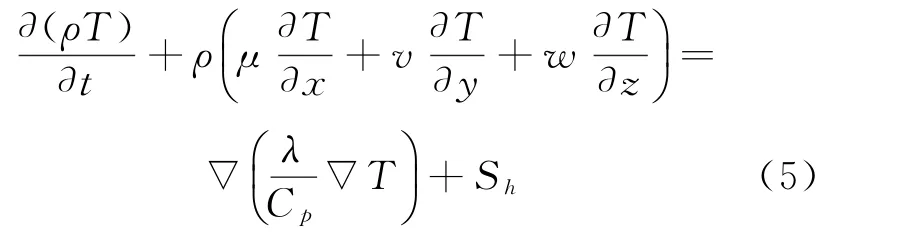
式中:∇2为拉普拉斯(Laplace)算子;∇为哈密顿(Hamiltonian)算子;ρ为密度;t为时间;u、v、w分别为物体沿x、y、z三个方向速度;P为压力;μ为动力粘度;Sx、Sy、Sz为动量源项;λ为导热系数;Cp为定压比热容,T为温度,Sh为能量源项。

2 建模方法

不同的电子组件层级存在着不同的仿真建模方法,有些方法仅适用于特定模型,不具有普遍适用性,具有通用特性的主要有详细建模法和集总参数法,在芯片建模中常用的还有热阻网络法。

2.1 详细建模法

详细建模法是对仿真分析对象的各个组成元件均予以保留,以获得最接近真实情况的温度分布。详细建模法所得到的计算结果精度高,可作为其他热仿真建模方法的检验标准。在芯片和电路板建模中的应用分别为芯片封装的建模和电路板布线层建模。

目前的电子仿真软件都有和电子设计自动化(EDA)软件的接口,可从EDA软件中导入芯片封装及电路板的布线层、热过孔等信息。

2.2 集总参数法

在热仿真分析中,集总参数法是应用范围最广的建模方法,可以应用于不同层级的热仿真[6]。集总参数法忽略物体内热阻,将需要建模的组件等效成材料属性单一、内部热量分布均匀的实体块模型,只考虑物体与环境间的换热。建立集总参数模型时,需要物理模型尺寸和材料参数。其中,材料参数包括导热系数、密度和比热容。导热系数应用于稳态分析,密度和比热容应用于非稳态分析。求解集总参数模型的材料参数时,可根据组件各部分组成材料的含量与材料属性计算出其等效值。

2.3 热阻网络法

热阻网络法是以热阻来代替封装芯片的热流路径,进而通过解析法或有限元仿真计算模拟预测芯片的温度。常见的热阻网络模型有单热阻模型、双热阻模型、星形网络模型和DELPHI简化模型[8-9],其中双热阻模型在芯片热仿真中应用最广泛。

3 芯片建模与仿真

封装芯片作为电子设备中的主要热源,在散热设计时需要着重考虑。芯片封装的种类繁多,结构复杂,不同芯片之间的散热特性差异较大,因此其建模的精度对热仿真结果影响很大。本文以塑料焊球阵列(PBGA)封装芯片为例,对三种建模方法进行了仿真研究。

3.1 详细模型

封装芯片的详细模型一般应包含封装的布线层、过孔等信息。本例中,PBGA封装芯片详细模型的结构及组成参数从芯片设计EDA软件中导入,模型示意图如图1所示。各组成单元的物性参数如表1所示[7],封装内部的传热路径主要为热传导。

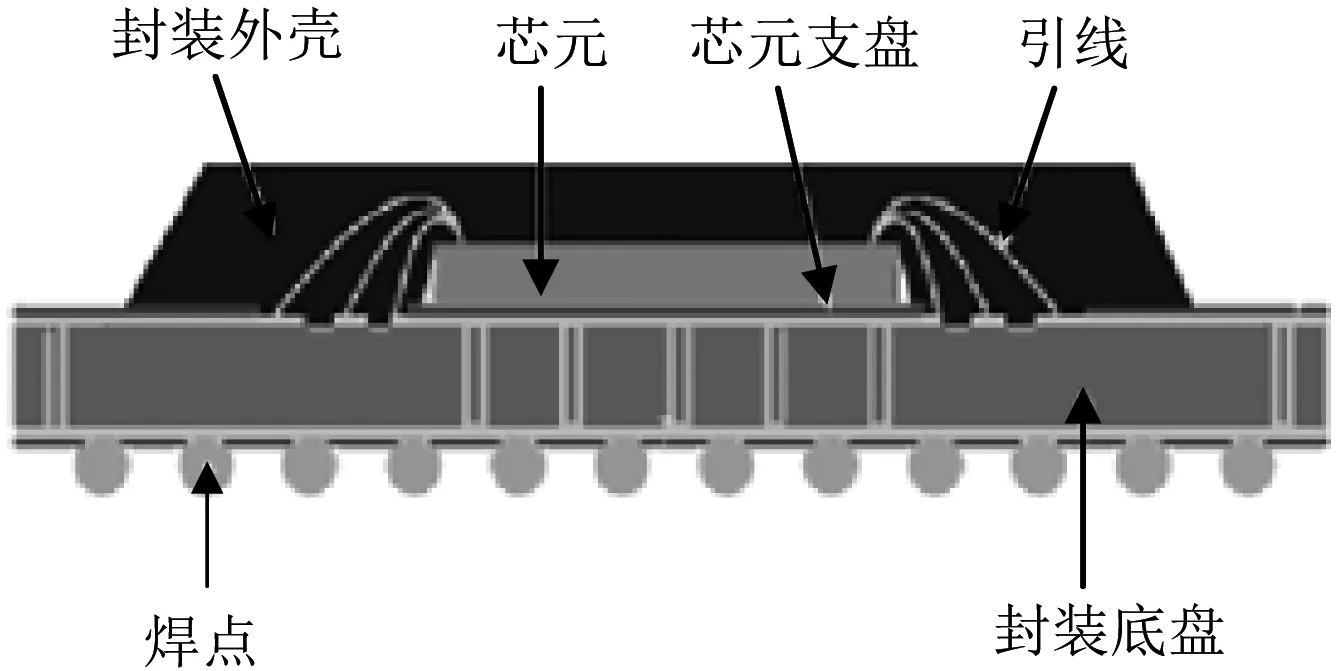
图1 PBGA封装模型示意图

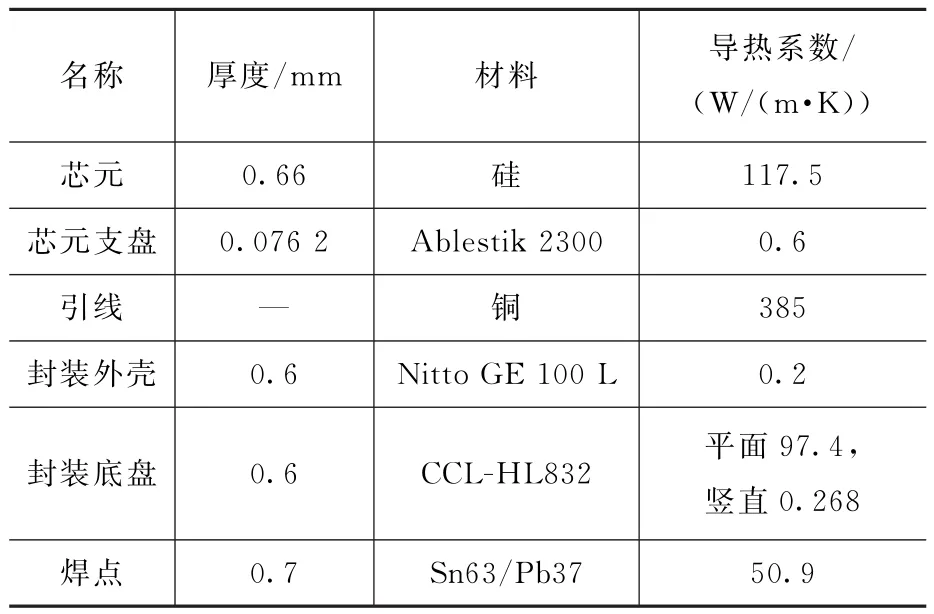
表1 PBGA封装物性参数

3.2 集总参数模型

芯片的集总参数模型是将封装芯片看做一个材料属性和内部热量均匀分布的块。随着器件封装技术的发展,根据不同的封装类型及尺寸,不同厂商的器件基本都遵循通用的封装规格。FLOMERICS公司根据不同封装器件的构造特点,使用集总参数法得出了不同封装的材料属性,如表2所示。

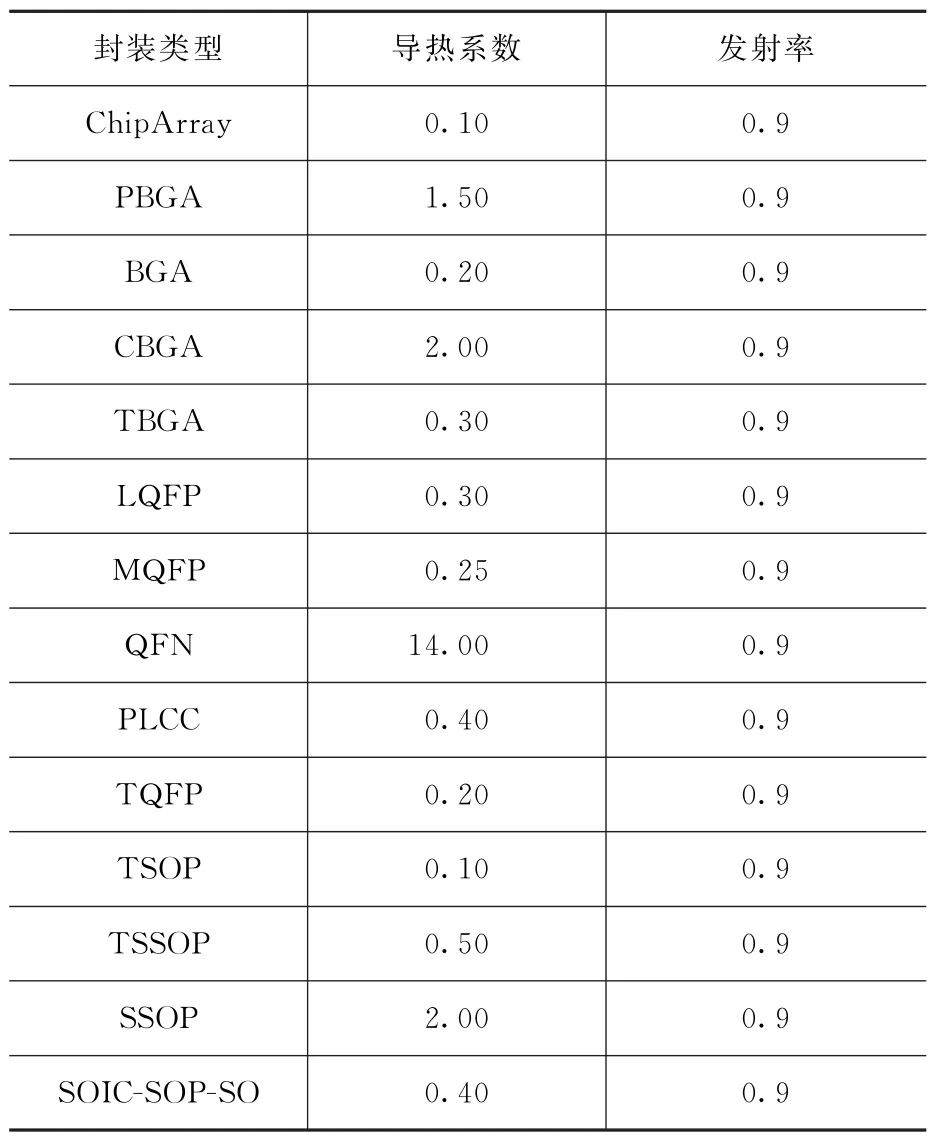
表2 不同封装集总参数法材料属性

3.3 热阻网络模型

PBGA芯片的双热阻模型,如图2所示。其中,Tj为器件的结温,Tc为芯片封装外壳的温度,Tb为芯片封装外部引脚与电路板相接处区域温度,Rjb为结到板的热阻,Rjc为结到壳的热阻,Q为芯片热耗。Rjb,Rjc和Q一般可由芯片手册获得。

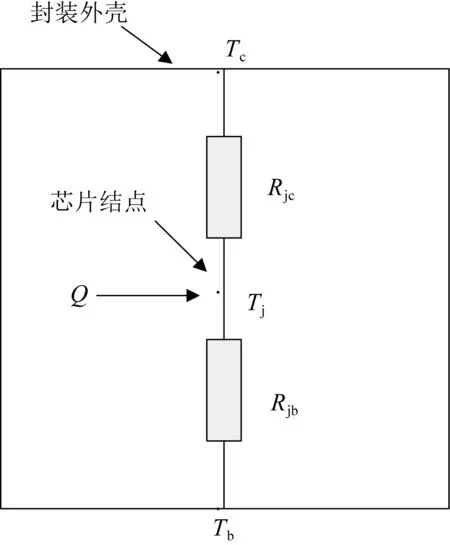
图2 双热阻模型

3.4 结果对比分析

本文仿真计算中,将芯片置于大小为150 mm×100 mm的电路板上,板平面导热系数为38 W/(m·K),竖直方向导热系数为0.35 W/(m·K),芯片热功耗为1 W。边界条件为环境温度25℃,自然对流散热,考虑辐射影响。图3给出了详细建模仿真获得的封装表面温度和芯片结温,图4和图5分别给出了集总参数模型和热阻网络模型温度云图,表3给出了芯片温度对比。

图3 详细模型温度云图

图4 集总参数模型温度云图

图5 双热阻模型温度云图

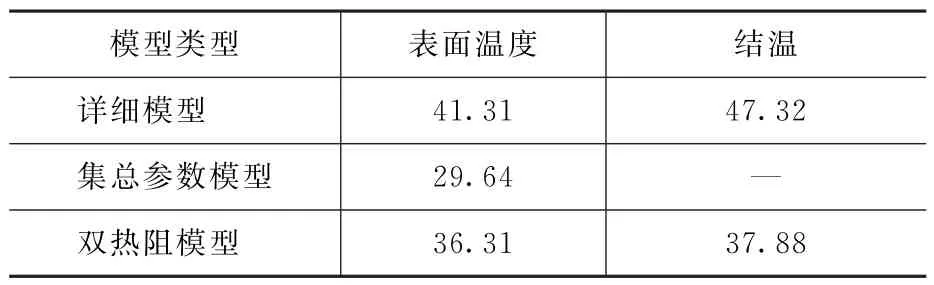
表3 芯片温度对比 ℃

由仿真结果可以看出:热阻网络法虽然不能表示封装内部的温度和热流,但可以得到封装的结温和表面温度;双热阻模型计算的封装表面温度和详细模型计算结果较为接近,结温的误差较大,可以应用于主要关注封装表面温度的板级和系统级热仿真中,或用于芯片结温的初步计算;集总参数模型精度较低,与详细模型计算结果偏差较大,适用于只关心表面温度的系统级热仿真中。在复杂的系统仿真中,可以采用热阻网络法和集总参数法结合的方式,热功耗大的芯片采用热阻网络法建模,损耗较小、作用较次的芯片采用集总参数建模。

4 电路板建模与仿真

电路板是电子设备中重要的热流通道,电路板模型的准确性不仅影响自身仿真结果,还会影响电路板上连接元件的仿真结果。目前在板级及系统级热仿真中,基于材料正交各项异性的集总参数建模方法较为常用,但该方法无法真实反映电路板间热流。本文针对电路板详细布线层模型和集总参数模型分别进行了仿真计算,芯片均采用集总参数模型,导热系数统一为1.5 W/(m·K),主要关注电路板模型对芯片表面温度的影响。

4.1 详细布线层模型

电路板内部结构复杂,层间铜的含量并非均匀分布,且包含一些散热孔和过热孔。详细布线层模型可以准确地描述电路板内部的热流情况以及板上组件的散热情况。图6为电路板的几何模型。本文建立的电路板详细模型通过EDA软件导入了布线层和热过孔信息,能够准确地反映电路板的导热率。

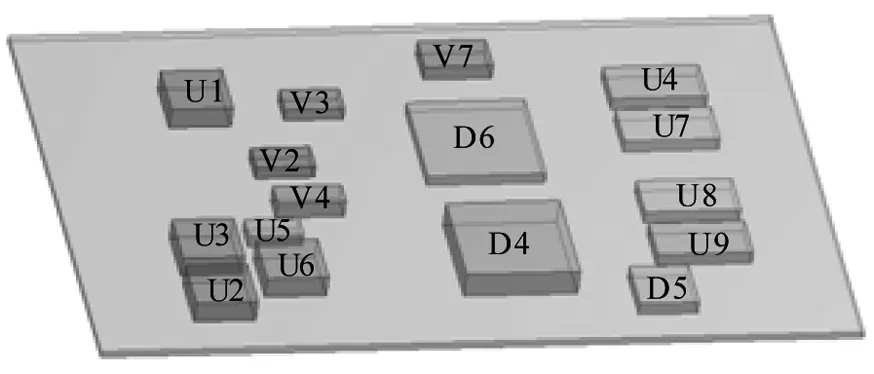
图6 电路板几何模型

4.2 集总参数模型

多层电路板主要由铜层和绝缘层组成,呈现出沿面板方向导热率较大,沿法向方向导热率较小的特性。集总参数建模就是将其看成一种正交异性材料,具有切向和法向导热系数。其导热系数分别为

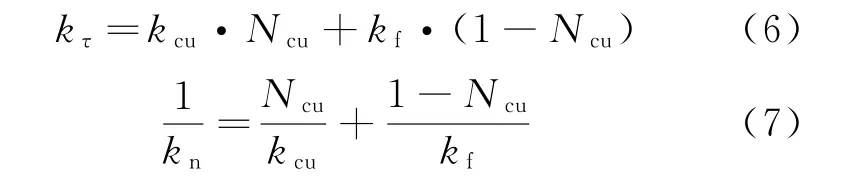
式中:kτ为切向导热系数;kn为法向导热系数;Ncu为铜所占体积百分比;kcu为铜的导热系数;kf为绝缘材料导热系数。

4.3 结果对比分析

设仿真的环境温度为25℃,散热方式为自然对流,考虑辐射影响。图7给出了两种方法的仿真温度云图。表4给出了电路板上关键芯片表面温度对比数据。

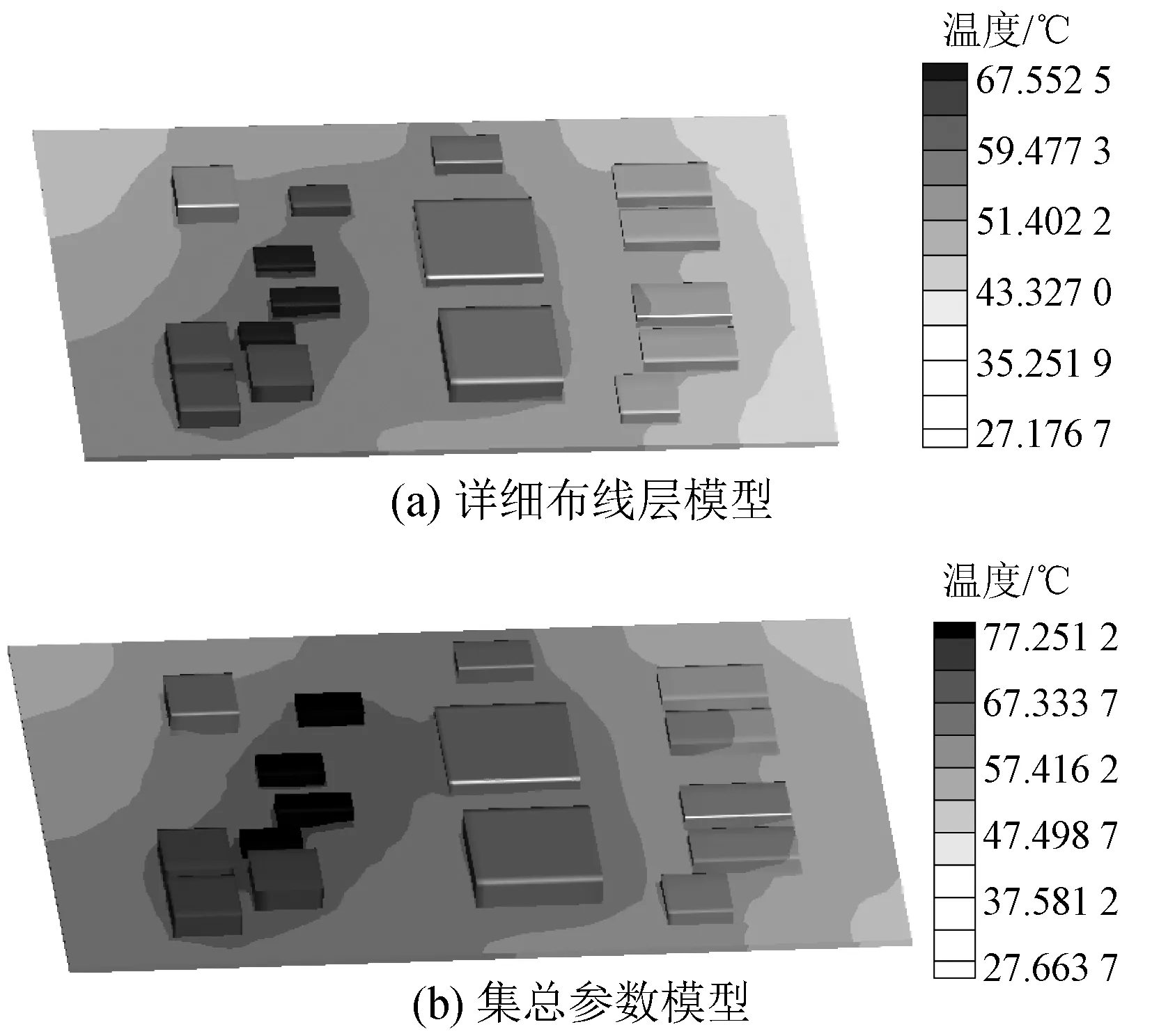
图7 电路板两种建模方法温度云图

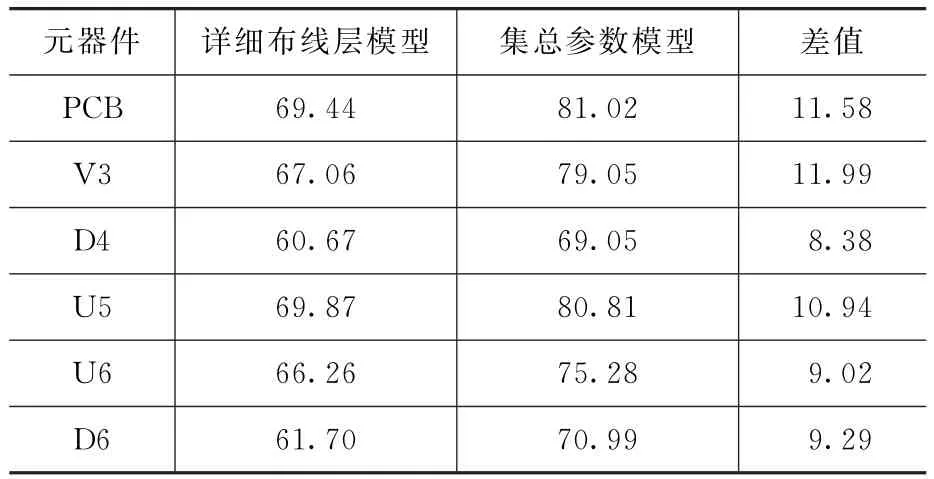
表4 关键元器件表面温度对比 ℃

由仿真结果对比可知,两种电路板建模方法得到的芯片表面温度差异较大。尤其在自然对流散热条件下,芯片主要通过电路板进行散热,最大温差可达12℃。详细布线层模型考虑了铜层的不均匀分布性以及层间过热孔对散热的影响,计算结果更真实。因此在对系统中某个电路板进行详细优化时,或对重要芯片进行热模拟时,应采用详细布线层模型。在大型的系统级的热仿真中,可采用集总参数模型。

5 电子单机建模与仿真

在系统级热仿真中,主要关注芯片及电子单机表面温度,以此来评估热设计的好坏。对于自主设计的电子产品,能得到其内部的详细信息,但对于外购的电子产品,内部结构信息常常缺失,只能得到物理外形模型。目前的仿真计算中都是将其简化成一个金属块,计算结果误差较大。且随着组件内部元器件复杂程度的增加,即使知道组件内部详细信息,建模的复杂度增加也会消耗大量的人力和计算机资源。因此在系统级热仿真中,必须要采用合理的简化模型。本文针对某电子单机进行了详细建模和集总参数建模对比分析。

5.1 详细模型

采用详细模型计算时,保留组件壳体及内部的电路板和元器件,忽略螺钉等细小特征,芯片采用双热阻模型,电路板采用详细布线层模型,计算模型外形图如图8所示。

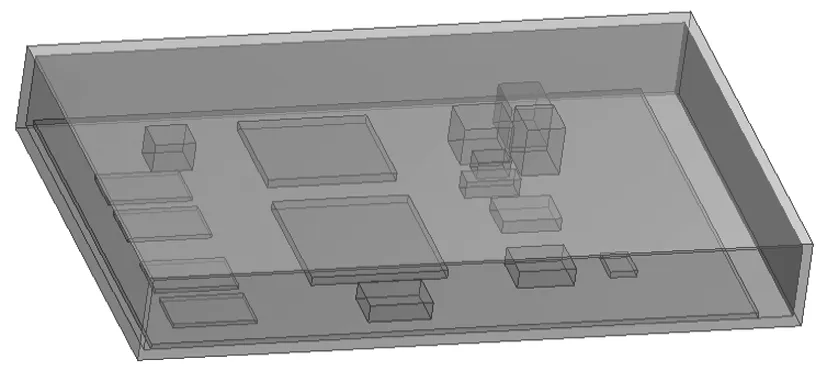
图8 详细模型外形

5.2 集总参数模型

集总参数模型将单机看做一个材料单一的实体块,根据单机的各组成零部件的材料,计算实体块的等效参数。本文仿真计算时,设密度为2 560 kg/m3,导热系数为110 W/(m·K),比热容为875 J/(kg·K)。在仿真计算时保持与详细模型相同的边界条件,将发热功率平均分布在实体上。图9给出了模型外形。

图9 集总参数模型外形

5.3 结果对比分析

设仿真边界条件为环境温度25℃,散热方式为自然对流,考虑辐射影响,总热耗为37 W,详细模型和集总参数模型网格数量分别为50万和10万。图10给出了详细模型外壳温度和内部芯片温度云图,图11给出了集总参数模型温度云图。

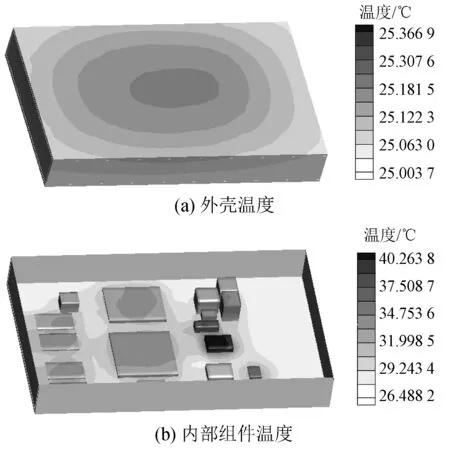
图10 详细模型温度分布

图11 集总参数模型温度分布

从图中可以看出,在集总参数模型中温度呈均匀分布,最高温度为45.078 3℃,位于电子单机表面。详细模型中最高温度为40.263 8℃,位于内部组件上,外表面最高温度为25.366 9℃,二者误差较大,主要原因是选取的等效参数不够合理。

集总参数法应用于孤立的组件热分析时,其仿真结果误差较大,但是对于复杂的电子设备,随着热流通道的增加和组件间的耦合效应增强,集总参数模型的相对误差会大幅降低。采用集总参数法时应尽量统计内部组件信息,对于内部组件严重缺失的电子设备,要与试验结果进行多次迭代,修正参数。在系统级的热分析中,对于重点关注的电子单机,可以采用详细建模方式,对于非重点部位或内部元器件严重缺失的单机,可采用集总参数建模方式。

6 总结

本文针对电子散热领域常见的热仿真建模问题,对不同层级的电子设备分别进行了等效建模方法研究,通过仿真结果对比分析,得到了不同建模方法的适用场合。主要结论有以下几点:

a)芯片的热阻模型和详细模型仿真结果相差不大,可以用于板级或系统级热分析中,集总参数法精度较低,可在复杂系统中用于功耗较小的芯片建模;

b)电路板采用集总参数模型和详细布线层模型仿真结果相差较大,在重点关注元器件温度时应采用详细建模方式;

c)集总参数模型无法得到器件内部温度,用于孤立的组件热分析时误差较大,但在系统级热分析中适用于内部元器件严重缺失的电子单机。