水泥生料立磨压差变参数二型模糊控制器设计
2020-08-24黄堃郑涛杨文
黄堃 郑涛 杨文


摘 要:大量仿真实例以及实际应用表明,二型模糊控制器的控制效果要优于PID、一型模糊控制器。虽然基于KM降阶算法并不能得到区间二型模糊控制器的解析解,但在特定的条件下,仍然可以得到一种非线性的区间二型模糊控制器的数学表达式。一旦二型模糊逻辑系统的结构确定下来,那么区间二型模糊控制器的形式也随之确定。水泥厂生料立磨粉磨系统具有非线性、大滞后、时变特性,传统的控制器难以得到理想的控制效果。提出了一种变参数二型模糊控制器设计算法,该控制器的参数在控制器作用过程中可变,因此该控制器的表达式可根据系统的响应做出合适的修改。通过对某水泥厂生料立磨压差控制的仿真结果表明,控制器能够在保证系统响应时间的基础上,降低系统超调,保持系统的稳定性。
关 键 词:立磨压差;二型模糊集合;二型模糊控制器;二型模糊逻辑系统;KM降阶
中图分类号:TQ 172 文献标识码: A 文章编号: 1671-0460(2020)04-0711-05
Abstract: A large number of simulation examples and practical applications show that type 2 fuzzy controller outperforms PID and type 1 fuzzy controller. Although the analytic solution of interval type 2 fuzzy controller cant be obtained by KM reduction algorithm, but under certain conditions, a mathematical expression of nonlinear interval type 2 fuzzy controller can still be got. Once the structure of type 2 fuzzy logic system is determined, the expression of interval type 2 fuzzy controller is also confirmed. The vertical roll mill grinding has the problems of nonlinearity, large time delay, and slow time-varying, and it is difficult for traditional controller to get ideal control effect. In this paper, type 2 fuzzy controller with variable parameter design algorithm was proposed, the parameter of which can be changed during the process of controller's operation. Therefore, the expression of type 2 fuzzy controller proposed in this paper can be modified appropriately according to the system response. The simulation results of differential pressure in vertical roller mill for cement-raw grinding show that, the methods can reduce system overshoot, ensure response time and maintain system stability.
Key words: Vertical roller mills differential pressure; Type 2 fuzzy set; Type 2 fuzzy controller; Type 2 fuzzy logic system; KM type reduction
中國水泥产量巨大,新技术新工艺发展迅速[1]。干法水泥生产中的其中一个关键环节是生料粉磨,其中应用最为广泛的是立磨,其磨粉效率高,能耗相对较低且具有良好的烘干能力。而立磨压差是磨机稳定运行的关键参数,目前常用的压差控制方式为PID控制器或者通过运行人员手工操作,根据经验和实时趋势判断需要设定的喂料量。但是由于粉磨系统的非线性、大滞后、时变特性,PID的控制效果不是很理想,人工调整的话又增加了工作量,影响了物料的质量和磨机的使用寿命。
随着二型模糊集合理论的发展,二型模糊逻辑系统实际中得到了很大应用,比如油罐液位控制[2]、发酵反应槽[3]、短期风速预测[4]、电力负荷预测[5]、污水处理过程溶解氧浓度控制[6]等。在实际操作过程中,二型模糊集合降阶过程,首先将二型模糊集合降阶为一型模糊集合,在利用合适的解模糊化的方法得到最终的精确量。由于降阶的复杂性,目前大部分的应用都是采用区间二型模糊逻辑系统,也有部分采用了普通二型模糊逻辑系统,但为了降低复杂性,该系统也是做了一些精简,比如应用于2轮移动机器人控制[7]、移动机器人控制[8]等。
由于大部分的区间二型模糊控制器都是采用Karnik–Mendel(KM)[9]降阶算法,该算法是一循环迭代过程,本身没有解析解。Wu针对一类区间二型模糊控制器,根据不同的条件下得到了区间二型模糊控制器的一般结构[10]。该表达式显示,区间二型模糊控制器为在结构上与传统的PI控制器类似,唯一的区别就是其参数是一非线性表达式且值与偏差的变化量有关。同时,文献[10]提出的区间二型模糊控制器的参数都是小于1的,这样能够有效降低系统的超调,但同时带来的一个问题就是系统响应速度的降低。
基于α平面描述的普通二型模糊集合降阶[11],为普通二型模糊控制器的设计奠定了基础。其核心思想为将普通二型模糊集合的降阶分解为若干个α平面表示区间二型模糊集合的降阶,这样可利用成熟的区间二型模糊集合降阶算法得到普通二型模糊集合的阶模糊化结果,大大化简了普通二型模糊集合降阶的运算复杂度。但是普通二型模糊控制器设计的一个重要问题是应该取多少个α平面,数量太多则会增加运算负担和控制器设计的复杂性,降低控制器的实时性。
如前描述的无论区间二型模糊控制器还是普通二型模糊控制器,一旦控制器的结构确定下来,则控制器的表达式就会确定下来。本文首先利用α平面理论,次隶属度函数选择三角型,将区间二型模糊集合扩展到普通二型模糊集合。选择α=1时的区间二型模糊集合作为降阶区间,得到了等价于PI控制器的二型模糊控制器。该二型模糊控制器具有多个可调参数,可根据对象的特性,通过参数调整获得较好的控制效果。其次,本文将提出的变参数二型模糊控制器应用于某水泥厂生料立磨压差的控制研究。通过与传统的PI控制器、传统一型模糊控制器、区间二型模糊控制器以及普通二型模糊控制器的控制结果相比较,本文提出的针对生料立磨压差的控制器具有较好的控制效果,无论是在超调量还是响应时间上,在几种控制器中都是最优的,为生料立磨压差的控制提供了一个新的思路。
1 二型模糊集合
误差和误差变化量首隶属度函数的端点分别为de和 ,通过偏移量d1和d2将一型模糊集合变成了二型模糊集合。由图2可以看出,本文二型模糊控制器共有4条模糊规则。
文献[15]利用KM降阶算法分析了区间二型模糊控制器的输出一般形式,得到了区间二型模糊控制器的数学表达式,分析了为什么区间二型模糊控制器具有较好的鲁棒性。文献[16]利用KM降阶算法提出了自整定的基于z切片的普通二型模糊PI控制器。但是KM降阶算法是一迭代过程,其并没有闭环表达式,且在实时控制中较为耗时。
3 本文算法
本文利用普通二型模糊集合的α平面表示方法,次隶属度函数采取三角型,如图3所示。
4.1 单位阶跃扰动
图4显示了在阶跃扰动下,本文提出的控制器与PI控制器、传统一型模糊控制器、区间二型模糊控制器,普通二型模糊控制器的系统输出响应曲线以及控制器的输出曲线。其中PI表示PI控制器的控制效果,T1表示一型模糊控制器的控制效果,IT2表示区间二型模糊控制器的控制效果,GT2表示普通二型模糊控制器的控制效果。
4.2 单位阶跃扰动:向上扰动
图5显示了在当系统设定值发生变化,且向上扰动的时候,本文提出的控制器与PI控制器、传统一型模糊控制器、区间二型模糊控制器,普通二型模糊控制器的系统输出响应曲线以及控制器的输出曲线。
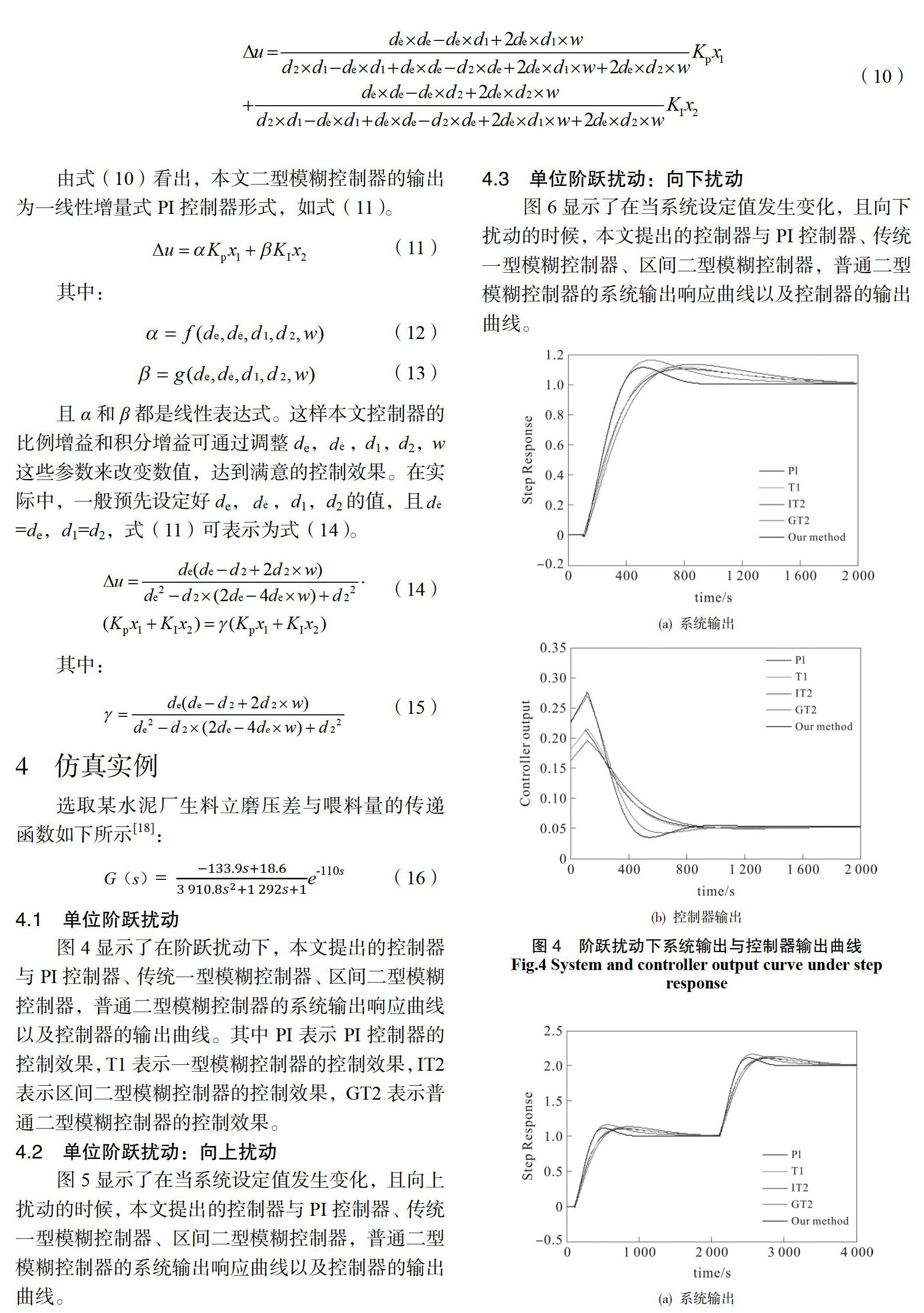
4.3 单位阶跃扰动:向下扰动
图6显示了在当系统设定值发生變化,且向下扰动的时候,本文提出的控制器与PI控制器、传统一型模糊控制器、区间二型模糊控制器,普通二型模糊控制器的系统输出响应曲线以及控制器的输出曲线。
5 结论
本文提出了一种等价于PI的二型模糊控制器,该控制器为一线性表达式,具有5个可调参数。与区间二型模糊控制器不同,本文控制器基于普通二型模糊集合的α平面表示方法,利用α=1平面的次隶属度区间进行计算,对于三角型次隶属度来说,其实就是一个点,这样本文的二型模糊控制器简化为传统的一型模糊控制器。推导出了最终的控制器输出的表达式,与PI控制器、一型模糊控制器、区间二型模糊控制器相比,本文的二型模糊控制器比例增益和积分增益均为线性可调。通过对某水泥厂生料立磨压差的仿真结构表明,本文提出的控制器与其他控制器相比,超调量较小,效应时间较快,具有较好的控制效果。
参考文献:
[1]黄雯昕, 孙晓燕, 王斐, 等. 硅酸钙生物活性水泥的研究与应用进展[J]. 现代化工,2017, 37(05):52-55.
[2]Wu D, Tan W W. A simplified type-2 fuzzy logic controller for real-time control[J]. ISA Transactions, 2006, 45(4):503-516.
[3]Ant?o R, Mota A, Rui E M. Model-based control using interval type-2 fuzzy logic systems[J]. Soft Computing, 2016, 22(6):1-14.
[4]郑高,肖建,王婧,等.基于区间二型模糊逻辑的短期风速预测研究[J].太阳能学报,2011,32(12):1792-1797.
[5]郑高,肖建.基于区间二型模糊逻辑的电力负荷预测研究[J].电机与控制学报,2012,16(9):26-32.
[6]韩红桂,刘峥,乔俊飞.基于区间二型模糊神经网络污水处理过程溶解氧浓度控制[J].化工学报,2018,69(3):1182-1190.
[7]Wagner C, Hagras H. Toward General Type-2 Fuzzy Logic Systems Based on zSlices[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(4):637-660.
[8]Kumbasar T, Hagras H. A Self-Tuning zSlices-Based General Type-2 Fuzzy PI Controller[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(4):991-1013.
[9]Karnik N N, Mendel J M. Centroid of a type-2 fuzzy set[J]. Information Sciences, 2001, 132:195-220.
[10]Wu D. On the Fundamental Differences Between Interval Type-2 and Type-1 Fuzzy Logic Controllers[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(5):832-848.
[11]Mendel J M. General type-2 fuzzy logic systems made simple: a tutorial[J]. IEEE Transactions on Fuzzy Systems, 2014, 22 (5): 1162-1182.
[12]王飞跃,莫红.关于二型模糊集合的一些基本问题[J].自动化学报,2017,43(7): 1114-1141.
[13]Mizumoto M. Realization of PID controls by fuzzy control methods[J]. Fuzzy Sets and Systems, 1995, 70(2–3):171-182.
[14]施建中, 李荣, 杨勇.一类区间二型模糊PI控制器设计算法[J].智能系统学報,2018,13(5):836-842.
[15]Wu D. On the Fundamental Differences Between Interval Type-2 and Type-1 Fuzzy Logic Controllers[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(5):832-848.
[16]Kumbasar T, Hagras H. A self-tuning zSlices-based general type-2 fuzzy PI controller[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(4):991-1013.
[17]Jianzhong, S., Shaohua, L., Yong, Y. et al. An improved general type-2 fuzzy sets type reduction and its application in general type-2 fuzzy controller design[J]. Soft Comput,2019. https://doi.org/10.1007/ s00500-019-03889-5.
[18]宁艳艳,苑明哲,王卓.水泥生料立磨压差的广义预测PID控制[J].信息与控制,2012,41(03):378-383+390.
