三角函数求值策略之“无中生有”

雷亚庆

(江苏省南京市大厂高级中学 210044)

一、无中生“1”

例1已知tanα=2，求sinαcosα的值.

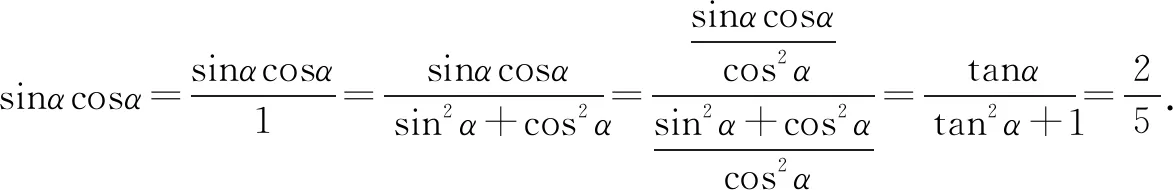
本题直接求解需要分类讨论，运算也会繁琐些，通过构造分母1凑出齐次式，可利用同角三角函数关系式直接转化为只含有tanα的式子，使问题顺利解决.

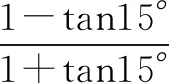
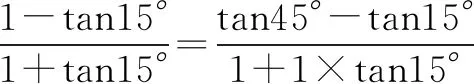
二、无中生“三角形”

例3 求sin238°+sin282°-sin38°sin82°的值.

解析构造△ABC,使得A=38°,B=82°,C=60°,设△ABC外接圆直径为2R,

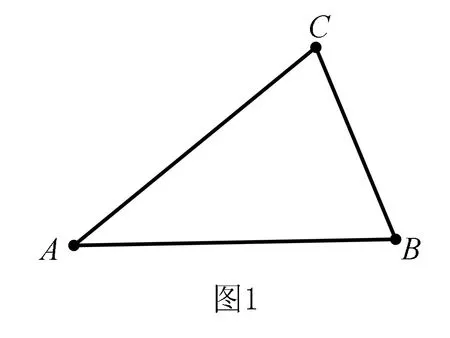
则：sin238°+sin282°-sin38°sin82°=sin2A+sin2B-2sinAsinBcosC.

由正弦定理：sin2A+sin2B-2sinAsinBcosC

反思如果利用三角公式进行化简和求值运算，需要降幂公式和和差化积公式，较繁琐，而且和差化积公式现在已经不学了.仔细观察所给角的特征我们发现38°,82°与60°正好构成一个三角形的三个内角，因此考虑构造三角形利用正余弦定理求解.实际上利用归纳推理，大家还可以得到一般性结论: 这实际上是正余弦定理的综合形式.

例4 求cos36°的值.

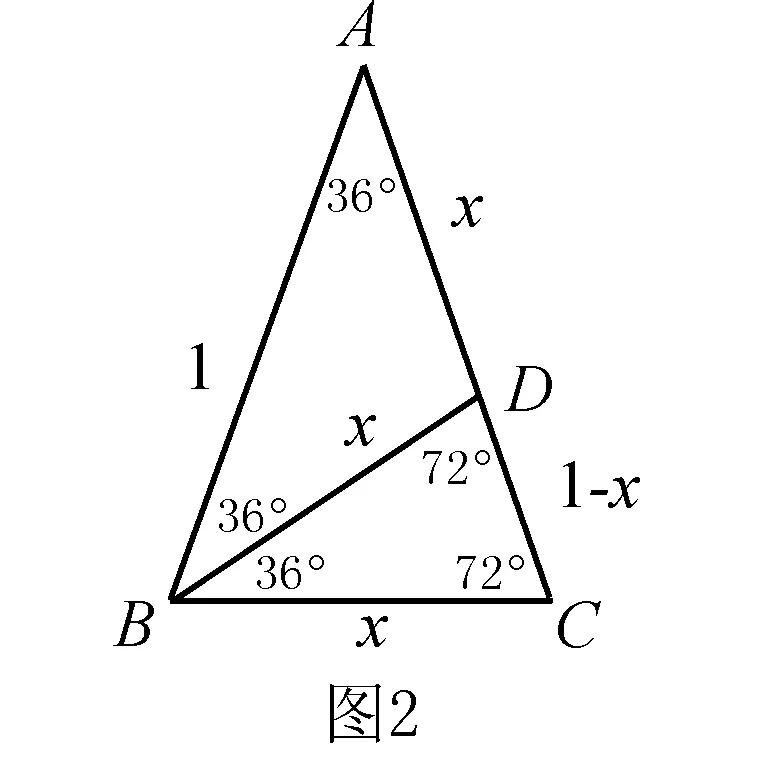
解析如图建立三角形ABC，∠A=36°,∠ABC=∠ACB=72°，

作∠ABC的角平分线BD.

设AB=AC=1,BD=AD=BC=x，则CD=1-x.

显然△ABC～△BDC,

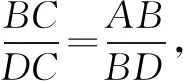
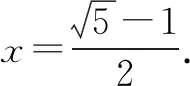
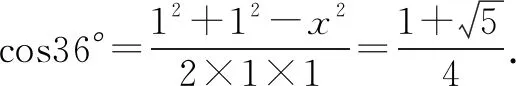
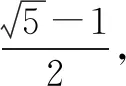
三、无中生“向量”

例4 求函数y=4cosx+3sinx的最大值.

解构造向量，设a=(4,3)，b=(cosx,sinx).

显然向量|b|=1，即向量b是单位向量.

因为a·b≤|a||b|,

所以有4cosx+3sinx≤5×1=5,

即函数y=4cosx+3sinx的最大值为5.

反思构造单位向量，利用a·b≤|a||b|求出函数最值.

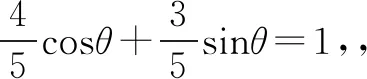
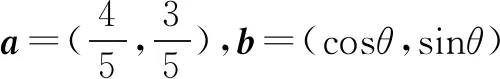
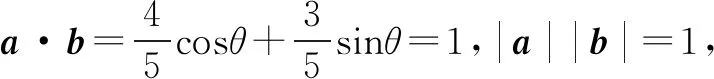
所以a·b=|a||b|.由此可得向量a,b共线同向,

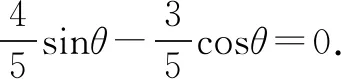
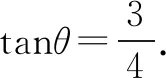
反思构造单位向量，利用向量数量积性质a·b≤|a||b|中等号成立的条件是向量a,b共线同向，从而使问题得以顺利解决.