寻找向量问题中的“圆”
2020-08-24俞新龙
数理化解题研究 2020年22期
俞新龙
(浙江省绍兴市柯桥区越崎中学 312050)
向量作为高考必考的知识点已经成为高考命题者尝试创新命题的一个重要阵地.近年来在高考和各省市模拟卷中出现了不少有新意的考题,其中有一些考题若能挖掘出题中隐含的“圆”,则问题便能较好的求解.下面举三例说明.

解析我们知道向量是数形结合体,故一般向量问题都会有两种解决办法:代数法和几何法.下面我们就从这两个方面来进行求解.
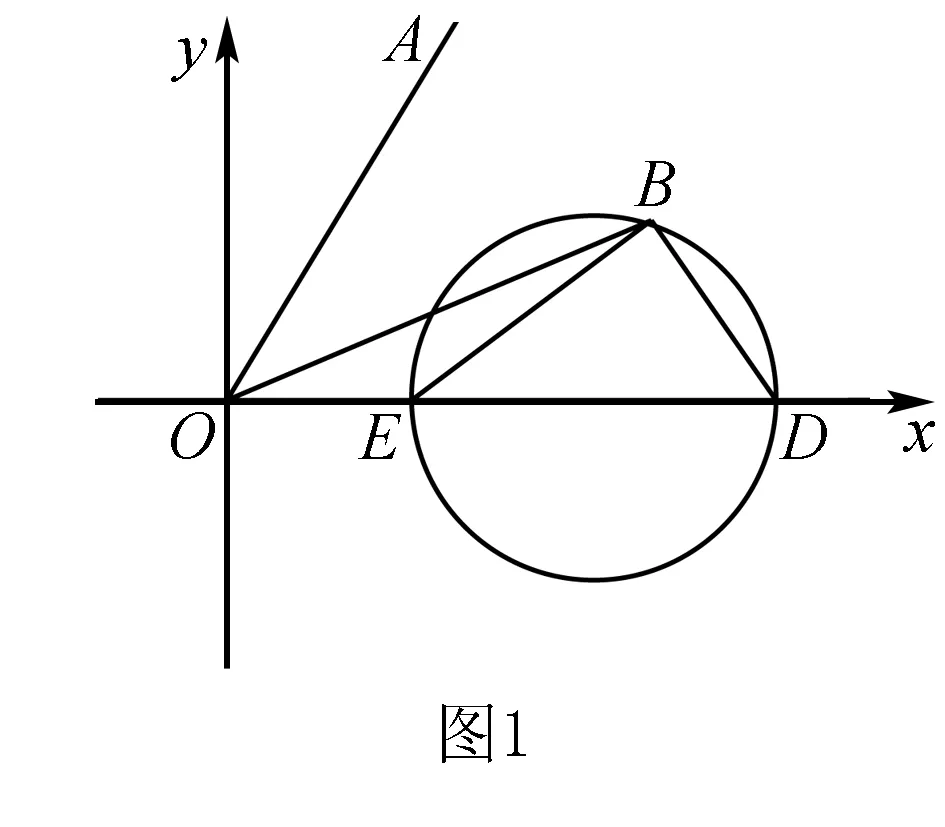
故答案为A.
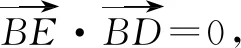
评注代数法中的圆从方程中能够直观得到,但几何法中的圆需要结合直角三角形直角顶点一定在以斜边为直径的圆上这个性质.
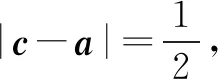


评注阿波罗尼斯圆的正用不难,难的是逆用甚至变用,一般求两条比例为1:λ(λ≠1)的线段和就可以试着用阿波罗尼斯圆的性质进行求解.
例3 已知平面向量a,b,c满足|c|=4,a·(c-a)=b·(c-b)=3,当a与b的夹角最大时,a·b=____.

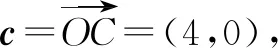
评注配方是个难点,从配方式子中看出轨迹是圆是关键点.
