再谈解题辩证法
2020-08-24甘志国
甘志国
(北京市丰台二中 100071)
发表于贵刊2019年第3期第2~5页的拙文《解题辩证法》从“有时需要把简单化为复杂来解题、拼角和拆角、设而不求与设并且求、不变(静止)与变化(运动)”四个方面阐述了解题辩证法,下面再从另外的三个方面续谈解题辩证法.
一、分离参数与分类讨论
题1(2014年高考课标全国卷Ⅰ理科第11题即文科第12题)已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(-∞,-2)
C.(1,+∞) D.(-∞,-1)

用导数容易作出曲线y=3x-x3如图1所示.

图1
由图1可得答案是B.
解法2(分类讨论)B.可先得a≠0.再得f′(x)=3x(ax-2).
若a>0,可得函数f(x)在(-∞,0)上是增函数(因为此时f′(x)>0),而f(-1)=-a-2<0,f(0)=1>0,所以此时f(x)有负数零点,不满足题意.
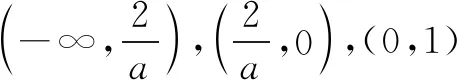
所以所求a的取值范围是(-∞,-2).
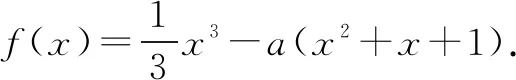
(1)若a=3,求f(x)的单调区间;
(2)证明:f(x)只有一个零点.
解(1)略.
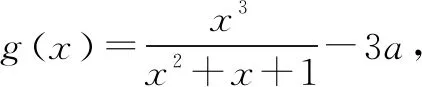
因而g(x)至多有一个零点,即f(x)至多有一个零点.
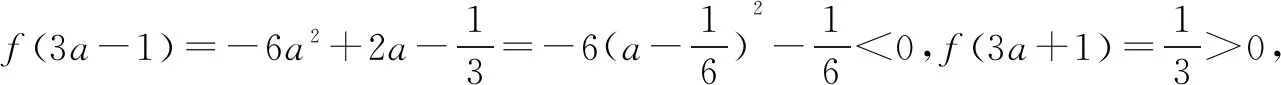
(2)的另证 (分类讨论)可得f′(x)=x2-2ax-a,其判别式Δ=4a(a+1).
当x>max{1,9|a|}时,可得0 a(x2+x+1)≤|a|(x2+x+1)≤3|a|x2, -a(x2+x+1)≥-3|a|x2. 所以0 a[t2+(1-t)]≥-|a|[t2+(1-t)]≥-|a|t2, -a[t2+(1-t)]≤|a|t2. 因而f(x)存在零点. ①当Δ≤0即-1≤a≤0时,f(x)是增函数,进而可得函数f(x)有且只有一个零点. 所以当a>0时,f(x)极大值<0;当a<-1时,f(x)极小值>0,因而当Δ>0时,三次函数f(x)均有且只有一个零点. 综上所述,可得欲证结论成立. 题3(2016年高考全国卷Ⅲ文科第21题)设函数f(x)=lnx-x+1. (1)讨论f(x)的单调性; (3)设c>1,证明当x∈(0,1)时,1+(c-1)x>cx. 解(1)(2)略. (3)设g(x)=1+(c-1)x-cx,可得g′(x)=c-1-cxlnc. 当x 又因为g(0)=g(1)=0,所以当0 即当x∈(0,1)时,1+(c-1)x>cx. (3)的另证 设g(x)=1+(c-1)x-cx(x∈R),可得g′(x)=c-1-cxlnc(x∈R)是减函数(因为c>1). 还可得g′(x)有唯一的零点(设为x0),进而可得g(x)在(-∞,x0),(x0,+∞)上分别是增函数、减函数. 再由g(0)=g(1)=0,可得当x∈(0,1)时,g(x)>0,即1+(c-1)x>cx. (3)的再证 设h(c)=1+(c-1)x-cx(c>1),可得 h′(c)=x(c0-cx-1)>0(0 所以h(c)是增函数,得h(c)>h(1)=0,1+(c-1)x>cx(c>1). 注题3(3)的第一种解法(即官方给出的参考答案)用到了题3(2)的结论(事实上,在官方给出的题3(2)的参考答案中,又用到了题3(1)的结论);题3(3)的后两种解法是“单刀直入”,均未用到前面的结论,反而更简洁更自然. 题4(2006年高考全国卷Ⅱ理科第20题)设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围. 解设g(x)=f(x)-ax=(x+1)ln(x+1)-ax(x≥0),g′(0)=1-a<0,可得题设即g(x)≥g(0)(x≥0)恒成立. 所以当g(x)(x≥0)是增函数即g′(x)≥0(x≥0)恒成立时满足题设. 可得g′(x)=ln(x+1)+1-a(x≥0),且g′(x)(x≥0)是增函数,所以当g′(0)=1-a≥0即a≥1时满足题设. 当a>1时,得g′(x)的零点为ea-1-1,且当x∈(0,ea-1-1)时,g′(x)<0,即g′(x)在(0,ea-1-1)上是减函数,得g(x) 当a>1时,也可不用找到g′(x)的零点ea-1-1来说明a>1不满足题意: 因为g′(x)(x≥0)是增函数,所以g′(x)的零点个数为0或1. 当g′(x)(x≥0)的零点个数为0时,由g′(0)=1-a<0知g′(x)<0(x≥0),g(x)(x≥0)是减函数,因而g(x) 当g′(x)的零点个数为1时,设其零点是x0,可得g′(x)<0(0 综上所述,可得所求a的取值范围是(-∞,1]. 题5 (2016年高考全国卷Ⅱ文科第20题)已知函数f(x)=(x+1)lnx-a(x-1). (1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程; (2)若当x∈(1,+∞)时,f(x)>0,求a的取值范围. 解(1)略. 当a≤2时,可得f′(x)>f′(1)=2-a>0(x>1),所以f(x)是增函数,得f(x)>f(1)=0(x>1),得此时满足题意. 当a>2时,可得f′(1)=2-a<0,f′(ea)>0,所以存在唯一的x0∈(1,ea)使得f′(x0)=0. 再由f′(x)是增函数,得当x∈(1,x0)时f′(x)<0,得此时f(x)是减函数,所以f(x) 当a>2时,也可不用找到f′(x)的零点x0(1 因为f′(x)是增函数,所以f′(x)的零点个数为0或1. 当f′(x)的零点个数为0时,由f′(1)=2-a<0知f′(x)<0,f(x)是减函数,因而f(x) 当f′(x)的零点个数为1时,设其零点是x0,可得f′(x)<0(1 综上所述,可得所求实数a的取值范围是(-∞,2]. 题6(2017年高考全国卷Ⅱ文科第21题)设函数f(x)=(1-x2)ex. (1)讨论f(x)的单调性; (2)当x≥0时,f(x)≤ax+1,求a的取值范围. 解(1)略. (2)设g(x)=ex(x2-1)+ax+1(x≥0),可得g′(x)=ex(x2+2x-1)+a(x≥0),g″(x)=ex(x2+4x+1)>0(x≥0),所以g′(x)是增函数,得g′(x)≥g′(0)=a-1(x≥0).当a-1≥0即a≥1时,可得g(x)是增函数. 因为题设即g(x)≥g(0)(x≥0), 所以当a≥1时,满足题意. 当a<1时,可得g′(0)=a-1<0. 当c≥max{1,ln|a|}时,可得c2+2c-1>1,所以g′(c)=ec(c2+2c-1)+a>ec+a≥|a|+a≥0. 因而存在正数d使得g′(d)=0,所以g(x)在[0,d]上是减函数,得g(x)≤g(0)=0(0 当a<1时,也可不用找到g′(x)的零点d来说明a<1不满足题意: 因为g′(x)是增函数,所以g′(x)的零点个数为0或1. 当g′(x)的零点个数为0时,由g′(0)=a-1<0知g′(x)<0,g(x)是减函数,因而g(x) 当g′(x)的零点个数为1时,设其零点是x0,可得g′(x)<0(0 综上所述,可得所求a的取值范围是[1,+∞). 定理(1)若f′(x)(x≥a)是增函数,则f(x)≥f(a)(x≥a)恒成立⟺f′(a)≥0; (2)若f′(x)(x≤a)是减函数,则f(x)≤f(a)(x≤a)恒成立⟺f′(a)≥0; (3)若g′(x)(x≥a)是减函数,则g(x)≤g(a)(x≥a)恒成立⟺g′(a)≤0. (4)若g′(x)(x≤a)是减函数,则g(x)≥g(a)(x≤a)恒成立⟺g′(a)≥0. 证明(1)当f′(a)≥0时,由f′(x)(x≥a)是增函数,可得f′(x)>0(x>a),f(x)(x≥a)是增函数,所以f(x)≥f(a)(x≥a)恒成立. 当f′(a)<0时: 由f′(x)(x≥a)是增函数,可得f′(x)(x≥a)的零点个数为0或1. 当f′(x)(x≥a)的零点个数为0时,由f′(a)<0可得f′(x)<0(x≥a),f(x)(x≥a)是减函数,f(x) 当f′(x)(x≥a)的零点个数为1时,设其零点是x0,可得f′(x)<0(a 综上所述,可得欲证结论成立. (2)同(1)可证. (3)在(1)的结论中令f(x)=-g(x)(x≥a)后,可得欲证结论成立. (4)在(2)的结论中令f(x)=-g(x)(x≥a)后,可得欲证结论成立.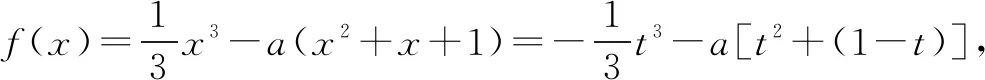
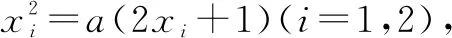
二、运用前一问的结论和直接解答该问
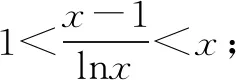
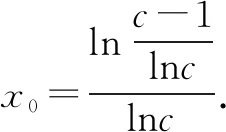

三、找点与不找点都是严谨解答