受载混凝土声波波速与应力关系的数值模拟
2020-08-24夏弋伟
夏弋伟
(武汉理工大学交通学院 武汉 430063)
超声无损检测在检测混凝土的损伤情况中已经广泛应用,但是在检测应力方向还有待发展。对于各向同性的材料(例如金属),应用超声无损检测手段测试其应力已经比较成熟,但是对于混凝土这种复合材料,由于其内部结构中有集料的存在,超声波在其内部传播的过程中将发生反射和散射,特别是粒径较大的骨料,对超声波的传播影响更大。国内外学者针对混凝土中超声波波速与应力大小关系做了许多研究,但研究多是以实验为基础,由于实验条件的限制,并不能得到理想的结果,利用数值模拟来探讨混凝土声波-应力关系的研究相对较少[1]。本文通过ABAQUS软件建立混凝土塑性损伤模型,模拟超声波在受载混凝土中的传播,以探究声波波速与应力大小的关系。
1 声波的传播规律及检测优势
声波在各向同性均匀介质中传播时,声速是一定的,但是当介质中有缺陷、裂纹或应力时,超声波在传播的过程中便会发生反射、折射等现象,会使接收到超声波信号的声速改变,通过对超声波信号的分析可以读取超声波中携带的关于试件的损伤情况、应力水平等有效信息。
声波在传播的过程中会被吸收而逐渐减弱,这就是声波的衰减。扩散衰减、吸收衰减和散射衰减是造成声波衰减的3个原因,在固体中声波的衰减最弱,而在液体和气体中的衰减较强。吸收衰减和散射衰减主要与传播介质自身的性质有关,扩散衰减则主要和声源信号的强弱有关。
声波在介质中传播时穿透性好,且具有一定的方向性,可以使用超声探头进行定性的发射和接收。超声接收探头接收到的数据可以在计算机中实时显示,以实现材料的在线检测,检测方式简单、快捷、仪器携带方便,相对于其他测量方法,声波无损检测具有以下优势。
1) 声波无损检测具有光学检测的方向性,同时还具有较强的穿透性,探测深度最高可达数米。
2) 探测精度高,其可以检测的精度通常认为是超声波波长的1/2,在实际工程应用中可以探测到十分之几毫米的空气间隙。
3) 超声测量不会损伤构件表面,检测时可以只从一个表面接触被检验的构件,能适应不同场合条件下的检测。
4) 超声测量仪器便于携带,使用简单,测量结果快速、准确。
2 混凝土模型的建立
2.1 混凝土塑性损伤模型
混凝土中存在的微裂缝、微孔隙称为混凝土的损伤。混凝土的破坏过程通常是由于微裂缝、微孔隙的扩展和累积造成,微裂缝的产生和扩展会引起混凝土非线性的应力-应变变化。混凝土塑性损伤模型是基于各向同性的假设,用各向同性的弹性损伤叠加各向同性的塑性形变来模拟非弹性行为,适用于混凝土受循环荷载时的情况,受力过程中考虑了刚度的退化及承受循环荷载后刚度的恢复。
模型建模采用混凝土塑性损伤模型[2],其应力-应变图见图1,当σ<σc0时,混凝土表现为线弹性,当σ>σc0时,混凝土开始出现损伤。在弹性范围内,超声波波速随应力的变化不大,由于混凝土塑性损伤模型及软件问题,较难识别该范围声速的变化,所以本文主要探讨混凝土出现损伤后声速的变化。在《建筑抗震弹塑性分析》[3]中,建议取1/3~1/2的峰值应变点为弹塑性分界点,本文取0.4。

图1 混凝土损伤塑性模型受压应力-应变曲线
2.2 混凝土二维随机骨料模型的建立
混凝土试件的设计尺寸为300 mm×250 mm×120 mm,标号为C30,集料使用为:质量分数为30%的粒径4.75~9.5 mm和质量分数为70%的粒径9.5~16 mm的玄武岩碎石,该混凝土试件的各组分用量见表1。

表1 混凝土各组分用量
在二维混凝土的模型建立时,通过Walraven公式将三维混凝土转化为二维混凝土模型。
(1)
式中:Pk为各粒径骨料总体积与混凝土试件体积之比;D0为骨料粒径;Dmax为最大骨料粒径。由式(1)计算得到2种粒径的集料在二维模型中所占的面积率:4.75~9.5 mm粒径集料占10.17%,9.5~16 mm粒径集料占8.03%。
从细观结构来看,混凝土是由砂、骨料、硬化的水泥浆,以及空洞和孔隙组成的非均匀多项复合凝聚体,简化后可以看成是水泥砂浆基体和骨料填充物组成的二项复合材料[4],在建模时混凝土二维模型分为3个部分,砂浆、骨料、砂浆与骨料的相邻界面。骨料采用6~10边的凸多边形,取骨料面积的1.05倍为界面,均匀厚度包裹于骨料外围。二维骨料采用蒙特卡洛法[5]随机投放,为了能够生成随机多边形,采用极坐标方法生成,并通过多边形的极半径和两极半径之间的夹角θi来描述。
γi=r+(2α-1)γ0
(2)
(3)
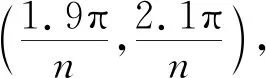
骨料生成后,需要将骨料随机投放到300 mm×250 mm的二维混凝土模型中,骨料形心坐标为
式中:α、β为(0,1)之间的随机数。在投放的过程中,不仅要满足投放的骨料在矩形内,还要使投放的骨料不能与任一骨料重合,骨料是否重合可通过式(4)判断。
D≥di+dj
(4)
式中:di、dj为i、j骨料的最大极半径;D为两骨料形心之间的距离。如果骨料重合,则应该重新生成骨料形心坐标,如果骨料不重合,则进行下一骨料的投放。
编写MATLAB程序生成随机的二维骨料的坐标后,将生成坐标于Auto CAD中绘出,见图2,保存文件后导入ABAQUS中生成二维混凝土模型。

图2 二维混凝土模型
3 模型静力分析
该模型中,由于骨料的强度高,在最大荷载下并不会出现损伤,所以采用线弹性模型来描述。随着荷载等级的增加,损伤开始出现在砂浆和界面处,所以采用混凝土塑性损伤模型来模拟砂浆和界面,对模型中涉及到的砂浆、骨料和界面3种料赋予其相关的材料属性,材料属性见表2。

表2 材料参数取值
添加边界条件,约束模型下边界的弯矩、位移和上边界的弯矩、水平方向的位移,在上边界添加荷载,每级荷载为1 MPa,最大荷载20 MPa。为满足超声波在混凝土中传播的精度要求,网格划分为1 mm。
由于在ABAQUS中不能实现应力场与声场的耦合,为模拟受载条件下的混凝土模型中超声波的传播,需要保存各个应力状态下的节点坐标,将应力下的节点坐标输入inp文件,重构混凝土模型,以模拟受载情况下混凝土的损伤情况。
由混凝土的塑性损伤模型可知其不同应力下的材料弹性模量,其计算方法见式(5)。
E=E0(1-d)2
(5)
式中:E0为材料的初始弹性模量;d为损伤因子。
在《混凝土的强度和变形试验基础和本构关系》[6]中提出,泊松比可由应变与峰值应变计算,其计算方式见式(6)。
(6)
但是由于ABAQUS软件的泊松比只能小于0.5,所以将式(6)改写,见式(7)。
(7)
由式(7)可计算出混凝土损伤塑性模型在不同应力下的弹性模量和泊松比,模型重构时,只需要将受力后的节点坐标保存,再计算出相应的弹性模量和泊松比,就可以模拟模型受力后的状态,以供后续声波传播模拟的使用。
4 受载混凝土声波传播模拟
4.1 声场的模拟
在声波模拟的过程中,发射声波采用能量较为集中的经HANNING窗调制的正弦波信号,发射频率为50 kHz,声波波形表达式见式(8)、式(9)。
F(t)=sin (2πfct)×h(t)
(8)
(9)
其中周期数n的选择应既能使能量集中,又能避免因周期数过多而导致信号重叠,从而对后期的分析造成影响,综上所述,周期数取5。声波激励信号通过动力显示以幅值的形式添加,在距发射点6.25 cm的竖直方向,布置1个参考点,将其与相邻节点耦合,做为信号接收点。激发点、信号接收点布置情况见图3。
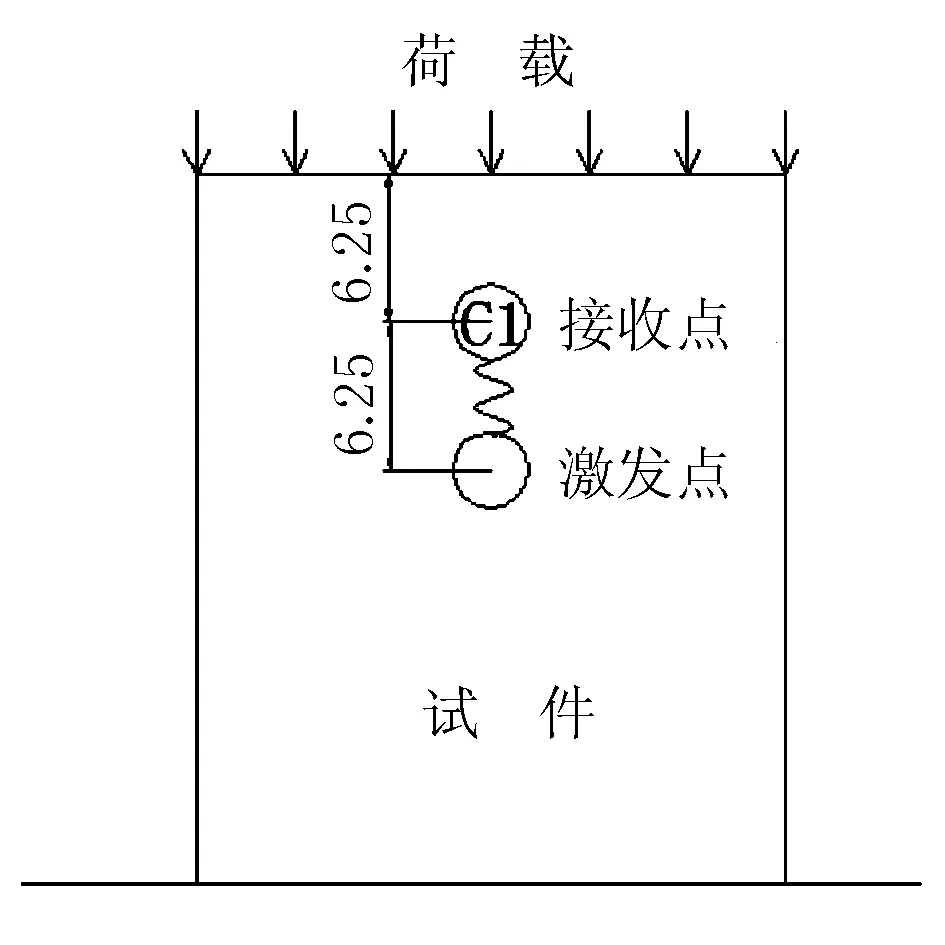
图3 激发点和信号接收点布置情况(单位:cm)
添加分析步时,时间步步长越短,计算越精确,但同时软件计算时间也会大大增加,故时间步步长通常取声波周期的1/20,静力分析时输出结果主要为应力场和损伤云图,声波模拟时输出结果主要为历程,定义位移和能量变量的输出,就可以绘出其与时间的关系,边界条件与模型静力分析时一致。
4.2 信号的分析
在声信号检测系统中,一个至关重要的环节就是对信号的采集和处理。
在接收探头接收声波信号时,首先要确定合适的采样周期T,取m为相关计算时的窗长,则对信号y1(t)的前m个采样点y1(0)~y1(m),y2(t)的前m个采样点y2(i)~y2(i+m)进行相关分析,通过i取0到信号采样长度的值,对2段信号进行相关计算,当相关系数最大时与之对应的iT即为两信号的时间差。其分析流程图见图4。

图4 相关性分析流程图
在对2组信号进行相关性分析时,对相关性分析结果影响较大的2个因素分别为采样频率和选取的窗口长度。采样频率的选择会直接影响到结果的精度,如果采样频率过大,会使信号采集时时间增加,计算量大大增加,给整个超声检测系统带来过大的负载,而且会使后期的计算量加大。如果采样频率过小,那么精度也会相应降低。窗口长度的取值会对相关系数曲线造成影响,窗口长度如果取得过短,则相关系数曲线的前端部分会比较平滑,窗口长度如果取得过小,则其相关系数的后端部分会过于平滑。如果取值不当,则会对相关系数峰值的确定造成不便。
通过MATLAB将采集的信号归一化处理后,再进行相关性分析,即可得出声波在混凝土中的传播时间。图5为应力20 MPa时采集的一组信号。

图5 20 MPa应力时的声波信号
由图5可见,声波信号在传播的过程中,波形不会发生改变,所以相关性分析法可以精确地计算声波的传播时间。
4.3 声速与应力关系分析
在超声波传播的过程中,纵波速度最快,所以信号接收点最先接收到的是纵波,而纵波波速与材料的弹性模量、泊松比和材料密度有关。
分别计算在不同应力下混凝土的弹性模量和泊松比,将不同应力下的节点单元坐标输入inp文件,重构混凝土模型,添加声场,计算出各应力下超声波波速,绘制应力比与声速比曲线见图6。
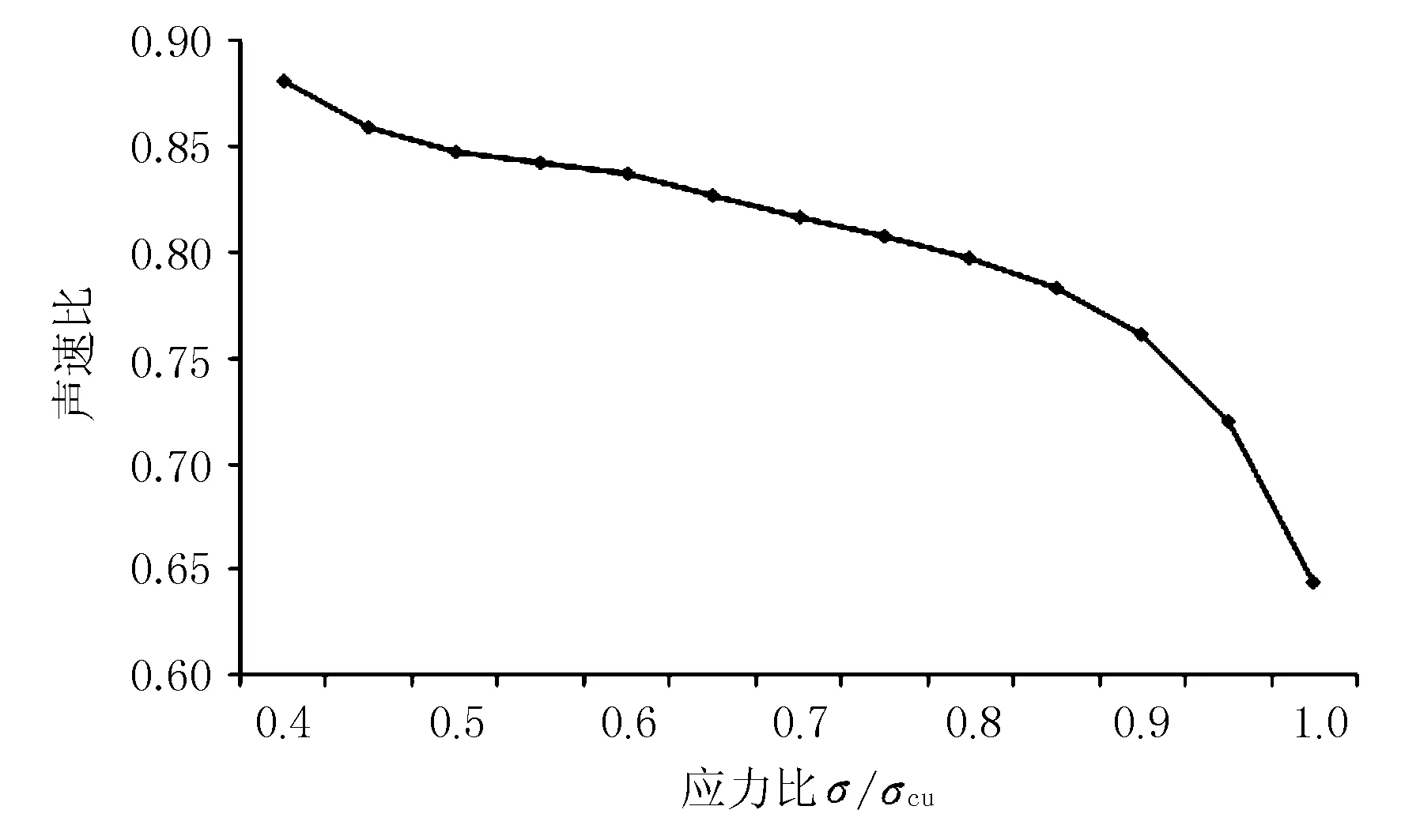
图6 应力比与声速比关系曲线
由图6可见,声波波速随着应力的增加整体呈现出下降的趋势。初始阶段,随着应力的增加,声速下降缓慢,但随着应力的逐渐增加,损伤开始增加,声速也开始急剧下降。
5 结论
混凝土中声速的变化规律根据应力大小可以分为3个阶段。
1) 在混凝土弹性阶段,及当σ/σcu≤0.4时,声速基本没有变化。
2) 当0.4<σ/σcu<0.8时,损伤开始出现,弹性模量开始减小,声速随着伤损的增加和弹性模量的增加开始不断减小,但此阶段混凝土的声速变化相对较小。
3) 当σ/σcu≥0.8时,混凝土的损伤大量出现,部分损伤开始连接成片,弹性模量减小,泊松比开始增加,声速开始急剧减小。在应力为20MPa、应力比接近1时,声速为零应力状态下的65%左右。
