基于差异变形控制的路基分幅间距研究

2020-08-24王力伟程梦筠蒋关鲁

交通科技 2020年4期

王力伟程梦筠蒋关鲁

(1.湖北省交通规划设计院股份有限公司武汉 430051；2.西南交通大学土木工程学院成都 610031)

近年来，随着中东部地区路网密度日趋饱和，国家政策开始倾斜于西部欠发达地区，而西部多地处沙漠、戈壁、草原地区，人烟稀少，交通量相对较小，二级公路建设速度较快，高速公路、一级公路路网密度略显不足，随着一级公路、二级公路取消收费政策的出台，考虑到建设资金的回收，收费公路(高速公路)的建设成为近期建设的重点。目前西部地区建设项目多集中于利用现有二级公路改建高速公路。

2011年，交通运输部发布《关于西部沙漠戈壁与草原地区高速公路建设执行技术标准的若干意见》[1]，该意见中对利用现有道路的原则、技术指标选取、后期运营维护管理等方面做了具体的规定，但对于利用现有二级公路作为高速公路半幅路基与新建半幅路基间距问题并未进行具体的规定。考虑到工程设计的需要，为了充分考虑各种因素，简化设计过程，有必要对分幅路基间距进行研究，提出合理的间距范围。

图1 分幅路基间距影响因素分析

由于既有路基变形已经基本稳定，新建路基填土荷载会引起既有路基基底两端产生不均匀附加应力，进而引起既有路基发生不均匀沉降病害，造成上部路面结构功能的损坏。因此，路线布设间距不宜过小，如目前柳墩路一期工程AK62+000-AK98+000段现有G215部分路段已出现路基纵向开裂及不均匀沉降病害情况。间距的选择应结合交通工程(防撞和防眩)的设置要求、土地资源占用、路基填土高度、地质条件，路基附加应力传递机理等综合确定。

文献[3]对在集中荷载作用的Mindlin解基础上，通过积分重新推导了在半无限体内部竖向矩形均布荷载作用于水平面内的应力解及作用在竖向面内时σz解的表达式。文献[4]基于弹性理论，推导了任意断面形式路基荷载作用下，过渡段地基及其临近影响地基内部任意一点的附加应力计算公式，分析了过渡段路基填筑对既有临近建筑物产生的影响。文献[5]通过对布辛奈斯克集中力下弹性半无限体的侧向变形解进行积分，分别推导出泊松比等于0.5和小于0.5时，无限长线性荷载、带状均布荷载、带状三角形荷载下侧向变形理论解。文献[6]通过三维有限差分数值模拟，分析新建公路跨线桥对既有高速铁路路基产生的附加影响(附加沉降和附加水平位移)，并对抑制这些附加影响采取的处治技术及对附加影响起主要作用的因素进行研究。

本文将对柔性路基荷载作用下，地基内任意一点地基附加应力计算公式进行推导分析，同时结合有限元计算，研究对不同填土高度下，新建路基填筑对既有路基产生附加影响的机理。

1 柔性荷载下地基附加应力分布理论计算

Boussinesq利用弹性理论解决了弹性半无限体表面作用一集中力时内部任一点的应力分布，计算示意见图2。其计算方法见式(1)。

图2 半无限空间弹性体表面受集中力作用

(1)

式中：P为集中力；z为计算点至表面垂直距离；R为计算点与荷载作用点距离。

将式(1)变换为积分形式。

(2)

式中：x1，x2和y1，y2分别为积分限；p(x,y)、p(x)、p(y)为均布荷载。

各组hucMSCs细胞培养72 h后，Western blot结果显示，与Control及PBS组相比，Piwil2-iCSC来源的外泌体干预组的hucMSCs细胞MMP2、MMP9蛋白表达量均明显升高，Control与PBS组之间差异无统计学意义（图7）。

纵向积分求解示意图见图3，横向积分求解示意图见图4。

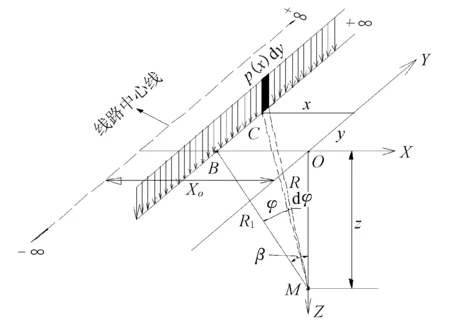
图3 纵向积分求解示意图

图4 横向积分求解示意图

应用三角函数关系推导

(3)

横断面上，荷载由三部分组成，σz1、σz2、σz3分别见图4中I号区域、II号区域、III号区域，则地基中任一点的附加应力由三部分荷载叠加而成，即

σz=σz1+σz2+σz3

(4)

1)σz1的公式推导

由x=z0tanβ，x=x1推得β=β1；x=x2，推得β=β2，故

(5)

式中：p为等代均布应力荷载。

2)σz2的公式推导

由x=z0tanβ，得

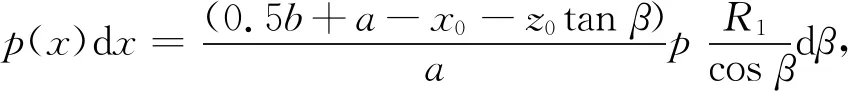
(6)

3)σz3的公式推导

由x=z0tanβ，得

(7)

sin(2β4)+(2β1-β4)]

2 附加应力空间分布形态分析

为分析不同填土高度下，新建路基填筑对既有路基应力的影响，采用式(4)分析不同路基填土高度下，附加应力竖向和水平向的分布规律。计算模型中取b=12 m，a=9 m。

不同填土高度下，距离坡脚不同位置处附加应力随深度的分布规律见图5。

图5 不同填土高度下，距离坡脚不同位置处附加应力随深度的分布规律

由图5可见，同一路基填土高度下，随着与坡脚的距离L的增加，地基附加应力逐渐减小，且最大地基附加应力出现位置逐渐下移，附加应力向更深处传递。因此，对于有软弱夹层的地基，应着重计算软弱层地基变形对路基沉降的影响。距离坡脚同一位置处，地基附加应力随深度变化呈现先增加后减小的趋势。

3 基于差异变形控制的有限元分析

为分析不同地基条件对分幅路基的影响，采用有限元计算软件Plaxis进行模拟分析。

假设地基为均质地基，为减小边界效应，模型计算宽度取300 m，深度100 m。

图6为距离坡脚不同距离位置处地基附加应力分布有限元和理论计算的结果对比，由图6可见，本文建立的计算模型和理论计算结果较为吻合。

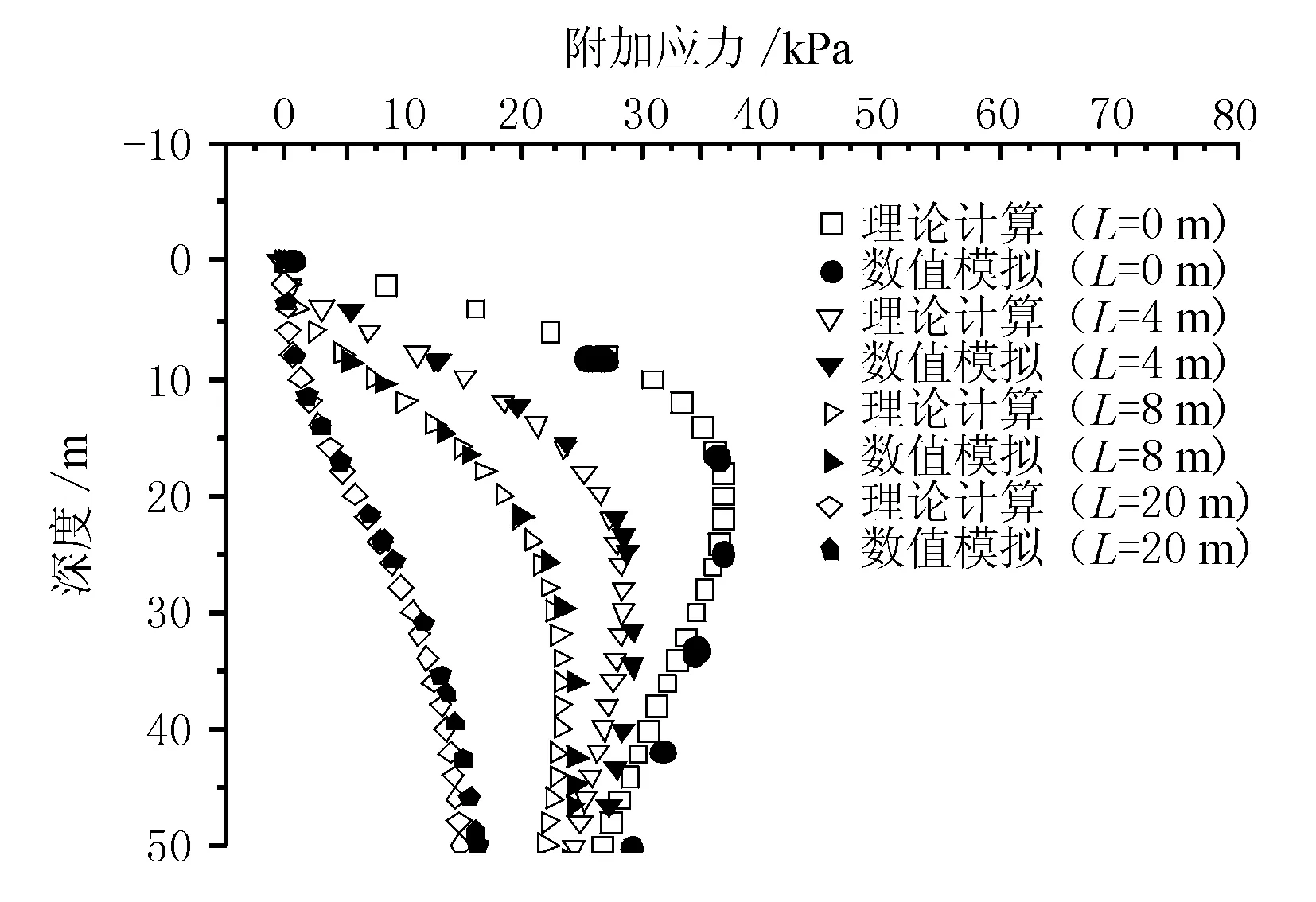
图6 距离坡脚不同距离位置处竖向附加应力分布(h=6 m)

不同深度处与坡脚不同距离处的竖向附加应力分布规律见图7。

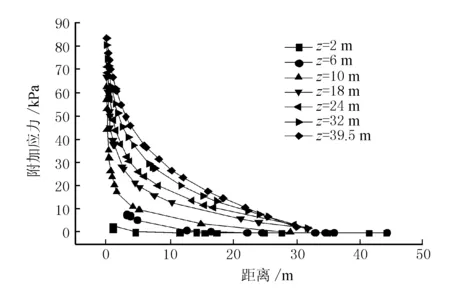
图7 不同深度处与坡脚不同距离处的竖向附加应力

由图7可见，同一深度处，地基附加应力随着距离坡脚距离的增加而逐渐减小，并趋于稳定；距离地表越近，附加应力收敛趋势越快。距离坡脚一定范围内，由于附加应力向深处传递，最大竖向位移出现在地表深处，既有路基两侧出现不均匀竖向变形，如不均沉降达到一定数值，将引起路面开裂，路基变形等病害。汪浩[9]、章定文[10]、刘汉清[11]等对加宽工程差异沉降的控制标准进行研究，得出路基差异允许变形在0.15%～0.4%之间。张军辉[12]对前述变形标准进行了分析，得出了0.25%的控制标准。本文以0.25%作为差异沉降控制标准。

为分析不同地基条件下，新建路基填筑对既有路基的影响，计算中采用了不同填土高度及地基变形模量，泊松比等参数来进行工况模拟。不同计算工况下既有路基的差异变形见表1。