基于非赫兹接触理论下的转体施工过程抗倾覆分析

尹耀霄 刘 争 刘 涛

(1.湖北交投智能检测股份有限公司 武汉 430000; 2.武汉马房山理工工程结构检测有限公司 武汉 430070;3.武汉理工大学土木工程与建筑学院 武汉 430070)

Hertz接触力学理论提出在正压力条件下获得了2个不协调的弹性球体表面接触应力的解析解[1]。从20世纪后期到现在，尽管非协调接触[2]的计算方法较为完善，但工程应用中仍大量存在协调接触[3]。转体桥[4-6](见图1)球铰的[7-8]上磨盘与下磨心即为协调接触，同时，球铰磨心表面的应力状态分布直接影响了转体施工(见图2)过程。但是公路桥涵施工技术规范的简化算法[9]中，球铰的相关计算均简化为平面，虽然减少了计算量，随之而来的应力误差也给转体过程带来了不可忽略的隐患。车晓军[10]在计算转体桥球铰时，将上下球铰曲面接触应力等效为均布力，虽然简化了计算过程，但是同时带来了应力分布与实际情况的误差。因为转动系统的抗倾覆能力由球铰的摩阻力矩提供，而摩阻力矩又是由球铰接触应力的分布计算得出，因此，研究非赫兹接触理论下的转动体系抗倾覆力矩计算显得尤为重要。

图1 转体桥上部结构

图2 转体施工示意图

本文引用非赫兹接触理论中Steuermann[11]的协调接触计算模型，并基于该模型推导出转动过程中的抗倾覆力矩，同时将基于简化算法的抗倾覆力矩、基于非赫兹接触理论下的转动体系抗倾覆力矩与实际测试数据进行比较分析，从而验证基于非赫兹接触理论下的转动体系抗倾覆力矩的计算准确性。

1 球铰失稳和抗倾覆系统

1.1 球铰失稳

桥梁转体过程中，失稳形式有2种，球铰示意及失稳示意见图3、图4。

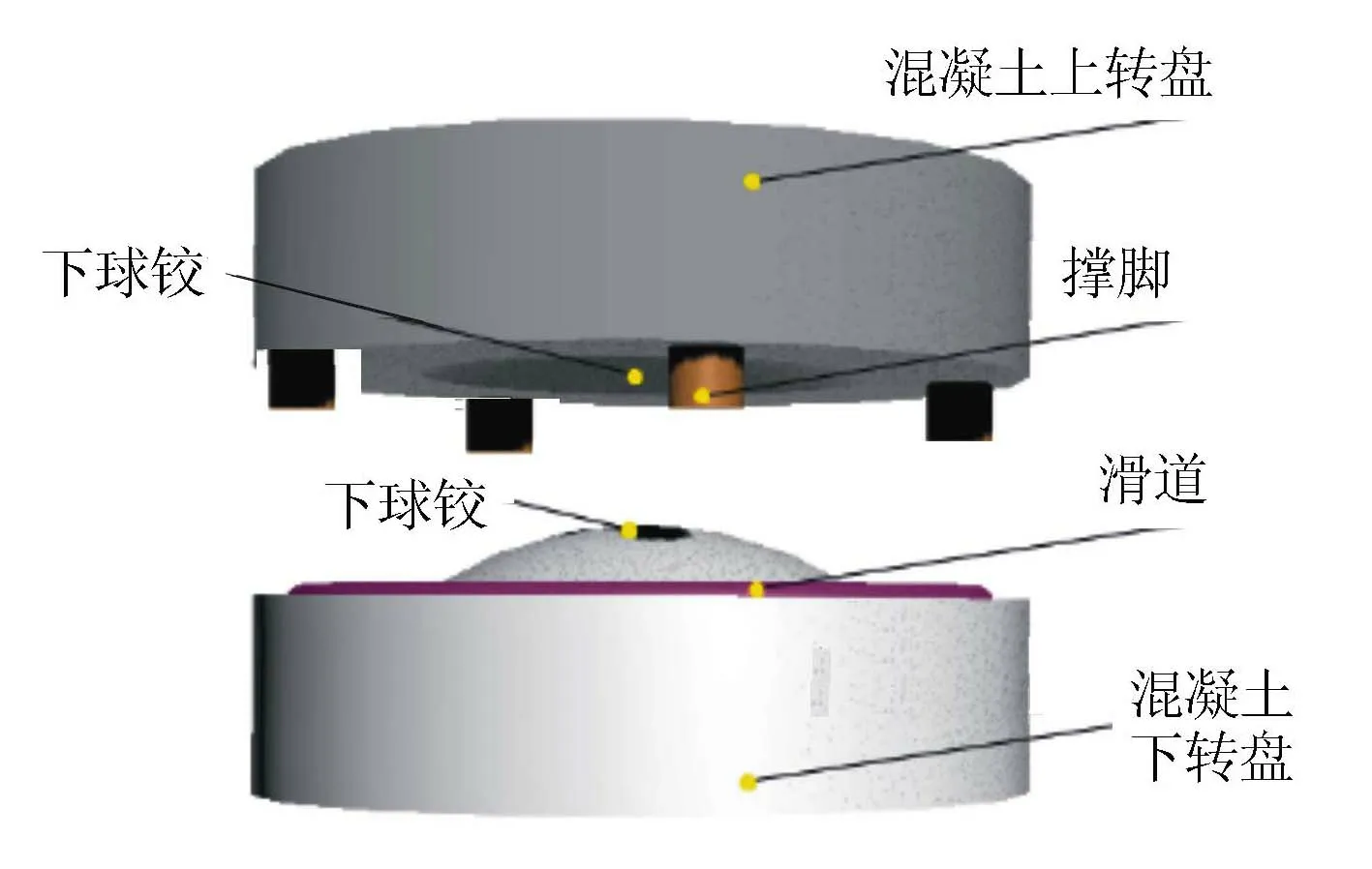
图3 球铰示意图

图4 失稳示意图

1) 球铰失稳。在撑脚未落地之前，整个桥梁梁体绕着球铰转动倾覆。

2) 撑脚支点失稳。撑脚落地，整个桥梁梁体绕着撑脚支点转动。

因撑脚摩擦力过大，并不利于桥梁转体的顺利进行，所以转体过程中尽量保证撑脚不从环道脱落。同时，由于撑脚支点失稳状态计算简单，因此，本文仅考虑球铰失稳状态。

1.2 抗倾覆系统

在转体过程中，转动体系的重心不在球铰磨心的圆心处，此时转动体系的偏心致使整个转动体系出现倾覆力矩，由于转动过程是转体桥施工中最为关键和危险系数最大的施工阶段[12]，因而转体过程中须实时监控整个转动体系的俯仰角变化，从而实时监控转动体系的倾覆力矩变化。其中倾覆力矩计算与背墙倾角关系示意见图5。

图5 倾覆力矩计算示意图

则倾覆力矩与背墙倾角计算式为

M1=Ge

(1)

e=lsinα

(2)

式中：M1为倾覆力矩，N·m；M2为抗倾覆力矩，即球铰摩阻力矩，N·m；e为偏心距，m；Fy为球铰支撑力，N；G为背墙的重力，N；l为转动体系重心高度，m；α为背墙倾角，(°)。

转体桥的抗倾覆系统由环形滑道、撑脚，以及定位销轴组成，其组成示意见图6。当转体桥的撑脚未触地时，其抗倾覆力矩由球铰磨心的摩阻力矩提供；当撑脚触地时，转动体系抗倾覆能力达到最大，此时撑脚为抗倾覆系统的最后一道屏障。

R-球铰半径;R′- 球铰平面半径;α-球铰支撑圆心角或球铰外边缘圆心角;θ- 球铰径向角度。图6 抗倾覆系统

2 非赫兹接触理论分析

2.1 球铰应力简化算法

在JTG/T F50-2011《公路桥涵施工技术规范》中，将球铰接触面简化成平面接触的计算模型，将球铰应力简化为平面均布力，用来计算两弹性无限半空间体，在物体表面相互接触时的接触应力。

球铰应力简化算法，接触表面应力分布可描述为

(3)

式中：F为转动体系重力，kN。

简化算法虽然简单，但是考虑到球铰处实际是曲面，受力情况比较复杂，所以简化算法得出的结果误差较大，不能真实反映球铰的应力分布。

2.2 非赫兹接触理论

非赫兹接触理论是相对于赫兹理论而命名的，非赫兹接触理论计算模型适用于协调接触，即两接触体的曲率中心在接触位置切面同侧，并且其曲率半径大小接近。Steuermann非赫兹接触理论的总荷载函数式及压力分布曲线分别见式(4)、式(5)。

(4)

(5)

式中：F为总荷载；a为接触带宽，mm；E*为当量弹性模量，MPa；A2为接触压力下接触带宽接触系数。

其中：

(6)

(7)

式中：E1、E2分别为两弹性体的弹性模量，MPa；μ1、μ2分别为两弹性体的泊松比；R1、R2为两接触面的上下半径，mm。

因此接触带宽a为

(8)

2.3 非赫兹接触应力工程应用

2.3.1工程背景

本文以恩施州南渡江转体拱桥(主跨190 m)施工为依托，以转体桥球铰磨心为研究对象，分别用简化算法、非赫兹接触理论及三维有限元仿真模型进行计算，分析其磨心处的应力状态分布，讨论非赫兹接触理论相对于简化算法就协调表面接触的合理性。

其球铰磨心部分尺寸，见图7，转体系统参数见表1。

图7 球磨心尺寸(部分)(单位：mm)

表1 转体系统参数

3 抗倾覆分析

3.1 临界抗倾覆力矩推导

3.1.1基于非赫兹接触理论抗倾覆力矩公式

转体球铰的几何形状示意见图8。

图8 球铰几何形状示意图

在微平面A上，有微平面摩阻力f1，则有

df1=μσds

(9)

式中：ds=R2sinθdθdγ；μ为摩擦系数，因此

df1=μσR2sinθdθdγ

(10)

可以推导抗倾覆力矩M2为

dM2=Ldf1=LμσR2sinθdθdγ

(11)

此时r2=x2+y2=(Rsinθ)2，所以有

(12)

所以整个体系最大的抗倾覆力矩为

(13)

式中：α为球铰球缺尺寸的下限(定位销轴的尺寸界线)；β为接触带宽所在球铰半径的上限。

3.1.2基于简化算法抗倾覆力矩公式推导

如果采用简化算法，即σ=F/(πR2)，则有

(14)

3.2 俯仰角追踪分析

南渡江拱桥转动体系现场布置俯仰角追踪系统，追踪背墙在转动过程中的倾角变化，用以实时判断转动体系的倾覆力矩的变化，在转动体系倾角较大时，实时对转动体系进行塔身倾角修正，保证转动体系工作安全、平稳、顺利。依据转体桥的转体施工要求，转体过程中处于无风状态，所以不考虑风载效应。

转动体系重心位置参数见表2。

表2 转动体系重心位置参数表

球铰半径R=8 500 mm，接触带宽1 248.42 mm，因此，θ的上下限α=arcsin(50/8 500)，β=arcsin(1 248.42/8 500)。将所有参数代入式(12)中，运用Mathematica计算可得，临界抗倾覆力矩(即摩阻力矩)为3 643.8 kN·m。现场测得背墙的倾角变化，通过式(1)、式(2)，可以实时计算出现场背墙X(顺桥向)与Y(横桥向)方向上的倾覆力矩，见图9。

图9 背墙倾角实时变化图

由图9可见，在365 min时，转体桥顺桥向出现最大倾角，此时运用式(1)、式(2)可得倾覆力矩达到最大值2 094.38 kN·m，由于该值小于运用式(13)计算出的抗倾覆力矩的临界值4 499.79 kN·m，也少于运用式(14)计算出的抗倾覆力矩临界值6 327.84 kN·m，可见基于简化算法的临界抗倾覆力矩比基于非赫兹理论的临界抗倾覆力矩增大了40.6%，该值的变化可防止由于临界抗倾覆力矩过大估计而导致的实际倾覆力矩大于临界抗倾覆力矩。所以在全桥转体过程中，转动体系的倾覆力矩在抗倾覆力矩值之内，转动体系在转动过程中处于安全状态。

4 结语

转体桥球铰在静止状态下，由于其上下球铰接触为协调接触，因此运用《公路桥涵施工技术规范》简化算法及非赫兹接触理论进行应力计算时，会出现应力分布的偏差，基于两者计算而得出的抗倾覆力矩有所不同，将两者结果与工程实测结果进行对比分析。结果表明，基于简化算法的抗倾覆力矩比基于非赫兹接触理论所得的倾覆力矩大40.6%，因此，基于非赫兹接触理论下的转体施工倾覆验算更符合实际计算结果。