高速公路中央绿化带滴灌系统设计参数对出流均匀度影响研究
2020-08-24付旭辉王文广涂光胜谭江涌
付旭辉,王文广,谭 华,涂光胜,滕 钢,谭江涌
(1.重庆交通大学 河海学院,重庆 400074;2.重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;3.重庆忠万高速公路有限公司,重庆 401147)
0 引 言
近年来,随着我国高速公路等基础设施的全面建设和智能化技术发展,滴灌技术以其节水、高效、智能控制、人工干预少等优势在高速公路绿化带灌溉系统中逐渐推广。为解决滴灌系统设计优化中存在的诸多问题,众多学者对滴灌管道水力特性进行了大量研究。
在滴灌管道水力特性理论研究方面,KANG Yaohu[1]等采用有限元法建立了滴灌毛管模型,基于Darcy-Weisbach公式确定了滴管水头与灌溉流量之间的关系。S.K.JAIN等[2]建立了进口水头与流量的冥函数关系史,并借此建立单管、多管等各种型式滴灌系统的设计方法。V.RAVIKUMAR等[3]采用经验公式分析了毛管流量及进口工作压力的关系,采用Darcy-Weisbach公式推求滴灌毛管的水力特征。孙永胜等[4]总结了低压滴灌系统的发展历史及管道水力特性的研究进展。白丹等[5]采用多元线性回归法推导了滴灌管沿程水头损失的计算公式。
在滴灌系统的水头分布及流量均匀性方面,冯素珍[6]通过试验和数值计算,提出滴灌系统平均工作压力水头与灌水均匀度之间并非简单的单调递增关系。洪明等[7]开展了低压条件下小管径PE管微孔口型滴灌管道水力性能试验,试验结果表明管内流态以层流为主,孔口局部水头损失与滴灌毛管的进口压力关系密切。王宏等[8]通过对低水头孔口式滴灌管进行了实验研究,结果与文献[7]的研究类似,均认为水力模型试验结果与规范中计算公式相差较大。张林等[9]认为低压条件下毛管进口水头的变化并不会对毛管灌水均匀度产生明显影响,合理管径是影响灌水均匀度的主要因素。张天举等[10]通过内镶式滴灌带和薄壁滴灌带毛管水力学试验,指出毛管铺设坡度和进口水头是影响毛管滴灌均匀度的主要因素。苏德荣等[11]认为自流式低压滴灌系统的滴头流量受压力影响明显,但只会延长灌溉时间而非灌水均匀度。
上述研究成果表明,针对滴灌系统已有丰富的研究成果,主要是基于Darcy-Weisbach公式理论推导或水工模型试验方法,研究了滴灌系统管径、水头、滴头分布、控制流量等参数对最终滴灌均匀度分布影响。但实际工程中,例如在忠万高速公路绿化带存在大比降、长距离、高水头等复杂边界条件下,缺乏明确可靠的解决方案。故有必要开展相应的滴灌管道水力特性研究,以保证工程的灌溉均匀性、有效性和稳定性。
1 工程背景
本研究依托忠万高速公路万州段绿化带智能灌溉示范工程。该工程位于重庆市万州区燕山出口段,全长500 m,包括坡面蓄水系统、自动控制系统、滴灌官网系统等。考虑当地的气象条件、土地使用规划、下垫面特性等特征[12-14],中央绿化带为两列灌木+铺地草被种植模式,灌溉模式采用变坡点两侧各布置2条PE-DN60灌溉毛管的型式轮流滴灌。路旁边坡处建108 m3蓄水池一座,蓄水池安装手动闸,处于常开状态。整套滴灌系统由太阳能供电,PLC系统气温和土壤湿度,实施滴灌过程自动控制。其灌溉管网具体参数如下:
1)1条往万州方向的灌溉段长250 m(起止桩号为K49+200—K49+450)、坡比1.20%;
2)1条往忠县方向的灌溉段长250 m(起止桩号为K48+950—K49+200)、坡比1.06%;
3)蓄水池至变坡点水头差约10.46 m(水面标高581.38 m,变坡点高程570.92 m),从蓄水池出水口到变坡点的输水管包括16.74 mPE-DN75管(蓄水池出水口-高速公路路肩)+250 mPE-DN75管(高速公路绿化带露头-变坡点)。从最不利角度考虑,输水管线段长度以280 m考虑;
4)各PE-DN50灌溉管道上,每隔固定距离接2个压力补偿式滴头,滴头工作压力为5~40 m水头,流量为8L/h;压力补偿式滴头再外接透明塑料软管,向中央绿化带供水;
5)蓄水池位于桩号K49+395.00处,直径8.7 m,深度2.5 m,总容积108 m3。池顶标高582.00 m,池底标高580.00 m,最高设计水位581.38 m,总蓄水体积85.78 m3;实际最低蓄水位约581.38 m。
针对忠万高速公路绿化带滴灌工程边界条件,笔者布置了室内水力学实验获得实测参数特征,采用基于MATLAB平台的迭代数学模型,分析了管长、管径、滴头间距、坡比等参数对最终出流均匀度的影响,为最终的管网设计提供依据。
2 数学模型
2.1 模型算法
为优化滴灌系统设计,获得滴灌官网内水力特性分布特征,笔者基于MATLAB平台,采用迭代逼近法和Darcy-Weisbach公式建立数学模型,推求沿程出流量均匀条件下管网内的水头分布特征,如式(1)。
(1)
式中:hf为沿程水头损失;λ为沿程水头损失系数,与水流流态有关;l为管长;d为管道直径;v为流速;g为重力加速度,g=9.81 m/s2。
根据尼古拉兹研究成果,沿程水头损失系数λ与管道相对光滑度有关。根据黏性底层厚度δ0与绝对粗糙度Δ关系,通常划分为光滑区、过度粗糙区和粗糙区,而λ的经验迭代计算如式(2):
(2)
式(2)中,Re为雷诺数,其计算如式(3):
(3)
式中:v为管内流速;d为管径;υ为水的运动黏滞系数,在20 ℃时,υ=1.007×10-6m2/s。
对于粗糙区而言,可用式(4)试算沿程水头损失系数λ。
(4)
根据曼宁公式(Manning),谢才系数C可用式(5)计算:
(5)
考虑滴灌管网采用压力补偿式滴头,假设沿程滴头处满足滴头额定工作水头要求,则毛管出流量为恒定值。以此假设,根据Darcy-Weisbach和沿程阻力系数公式可建立迭代求解数学模型计算管网沿程水头分布特征。
2.2 出流均匀度
滴灌系统孔口出流量的分布均匀性主要由均匀系数来进行定量评价,目前关于滴灌均匀性评价的计算公式主要为克里斯琴均匀系数(Christiansen)。灌溉均匀系数CU的计算主要由基于平均偏差所导出,如式(6)。
(6)
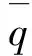
从克里斯琴均匀系数CU计算中可看出,该公式主要基于滴灌毛管沿程孔口处的流量值与平均流量值相比较的原理来综合评价滴灌均匀性。该均匀系数计算式理论简单,计算方便,经大量实践证明其科学性和合理性,已被广泛运用。因此,笔者以CU系数作为滴灌系统出流均匀度表征参数。
2.3 模型验证
为验证数学模型精度和可靠性,采用数模计算了初始水头为5.2、5.5、5.8 m条件下,单侧布置压力补偿式滴头的120 m长管的水头分布特征。同时,在模型试验场地布置了同样工况的水力试验,实测沿程水头分布和滴头出流量。将水力实验数据与数模计算成果进行对比分析,数据如图1。
从图1可见:设定边界条件的滴管沿程出流量,数模计算成果与试验成果趋势基本相符。除个别点因堵塞而偏差较大外,计算值与测量值偏差小于5%。由此可证明采用迭代逼近法的数学模型计算符合实际滴灌管网水力特征,且模拟误差基本在5%范围内,考虑植物生长需水要求,数模计算成果能满足设计精度要求。
3 计算结果分析
基于验证后的数学模型,针对滴灌管网系统滴头设置、管长、坡比、初始水头、滴头间距设计参数,以出流均匀度为判定标准,分析这些参数对均匀度的影响特征。一般而言,滴灌均匀度不小于75%[16],笔者以此为判断依据。
3.1 滴头对均匀度影响分析
本组试验对比采用克里斯琴均匀系数CU,对比大孔径薄壁出流、压力补偿滴头出流两种滴灌出流方式对均匀度影响。图2为两种出流方式的试验数据。
通过数值计算和水力学试验可看出:在不同进口初始水头条件下(5.2、5.5、5.8 m这3种工况),对应的孔口出流克里斯琴均匀系数CU分别为66.78%、67.23%、68.69%,而采用压力补偿式滴头的毛管出流均匀系数分别为92.44%、92.64%、92.70%,明显高于孔口出流型式的相应参数。从上述数据可看出:① 初始水头提高有助于提升孔口出流毛管的出流均匀性;② 压力补偿式滴头可显著提高滴灌毛管均匀度,减小滴灌系统对其它因素控制依赖。由此可见,在实际滴灌工程中采用压力补偿式滴头是提升滴灌均匀度的有效措施。故示范工程忠万高速公路绿化带中均采用压力补偿式滴头。
3.2 管道长度对出流均匀度影响
滴灌管道属于沿程多孔泄流的长管道,其管内水头压力、流量和孔口出流量均沿程变化,其水头损失主要体现为沿程水力损失系数。管道长度是影响毛管沿程水头损失的关键因素,而沿程水头损失对灌水均匀度产生一定影响,故管道长度与灌水均匀度的关系值得进行深入探讨。
笔者采用前述验证的数学模型,考虑边界条件坡度i=0.1%,滴孔间距S=0.8 m,研究不同进口压力水头(h=5、6、7、8、9 m这5种情况)条件下,毛管铺设长度对灌水均匀度影响。将计算得到的孔口流量代入公式计算得到灌水均匀度,绘制灌水均匀度与铺设长度的关系曲线,如图3。
由图3可知:在相同初始水头条件下,灌水均匀度随毛管铺设长度增大而线性降低。亦即毛管铺设长度越短,灌水均匀性越好;而管长越大,均匀系数越低。毛管在不同压力水头作用下,灌水均匀度在不同管长范围内的变化并不显著,变化曲线近似于线性。当管道长度大于60 m时,灌水均匀度可能会降至80%以下,超出植物灌溉均匀度要求。另一方面,在不同管长条件下,较高的初始水头度可获得较高的灌水均匀度。上述分析表明:在低水头条件下,较短的毛管长度可保证灌水均匀度要求。若工程条件需要长距离滴灌毛管,则需要适当增加初始水头及优化坡比、滴头间距等设计参数。
3.3 初始水头对出流均匀度影响分析
滴灌毛管进口初始水头压力会影响毛管沿程压力分布,必然也会影响孔口出流量的沿程分布特征,导致出流均匀度也随之变化。上述数学模型设置关边界条件为毛管长度L=120 m、滴孔间距S=0.8 m,研究一定坡比条件下(i=-1.0‰、0.0‰、1.0‰、5.0‰这4种坡度),不同毛管初始水头H(H=5、6、7、8、9 m这5种工况)对灌水均匀度CU的影响。将数值计算成果的毛管沿程孔口流量代入灌水均匀度CU计算公式,得到灌水均匀度与毛管初始水头的关系曲线,如图4。
由图4可知:在相同铺设坡度下,灌水均匀度与毛管初始水头呈正相关关系,即初始水头越大,灌溉均匀度越高。但灌水均匀度随压力变化(5~9 m)幅度较小,CU波动范围均低于5.81%。在坡度为-1.0‰、0.0‰、1.0‰、5.0‰这4种情况下,9、5 m水头(最大、最小水头)均匀度值变化幅度分别为5.81%、5.74%、5.67%、5.40%,均小于6%。由此可见:灌水均匀度对初始水头变化不敏感。亦即增加初始水头可略微提高灌水均匀度,但产生的影响效果有限。这一结论为前述学者进行低压滴灌技术研究给出依据,即低压滴灌系统设计优化可通过坡比、管径等参数的调整来实现。
另一方面,相似条件下初始水头越大、坡比越大,则灌流均匀度越大。也就是说,当实际工程由于管道长度较大而灌水均匀度不满足要求时,可通过适当增加初始水头来略微提高均匀度指标。在示范工程中,初始水头采用最高值,即10.68 m为额定水头,以提高滴灌系统出流均匀度。
3.4 滴头间距对出流均匀度影响
实际工程中作物种植所常用的株距是不同的,因此滴灌系统的出流孔口间距可以有不同选择。因此,根据灌溉植物、地形的差异,研究滴孔间距S对灌水均匀度影响有重要工程意义。采用前述数学模型,设置边界条件为毛管长度L=120 m、坡度为平坡(i=0.0%),研究一定初始水头条件下(H=5、7、9 m这3种情况),不同滴孔间距S(S=0.6、0.8、1.0、1.2 m这4种工况)对灌水均匀度CU的影响。将数学模型计算得到的孔口出流量代入灌水均匀度CU计算公式,得到灌水均匀度CU与滴孔间距S的关系曲线,如图5。
从图5可知:灌水均匀度CU与滴头间距S呈负相关关系,即滴头间距S越大,灌水均匀度CU越小。当滴头间距S从0.6 m增加到1.2 m时,在3种压力水头作用下,灌水均匀度变化幅度分别为40.79%、36.28%、33.09%,说明滴孔间距S的变化对灌水均匀度的影响较明显。一般来说,滴头间距越小,灌水均匀度越高。当滴头间距小于0.8 m时,灌水均匀度基本达到了80%以上,可满足规范要求。因此,滴头间距可作为提高灌水均匀度关键参数来进行设计优化,如表1。
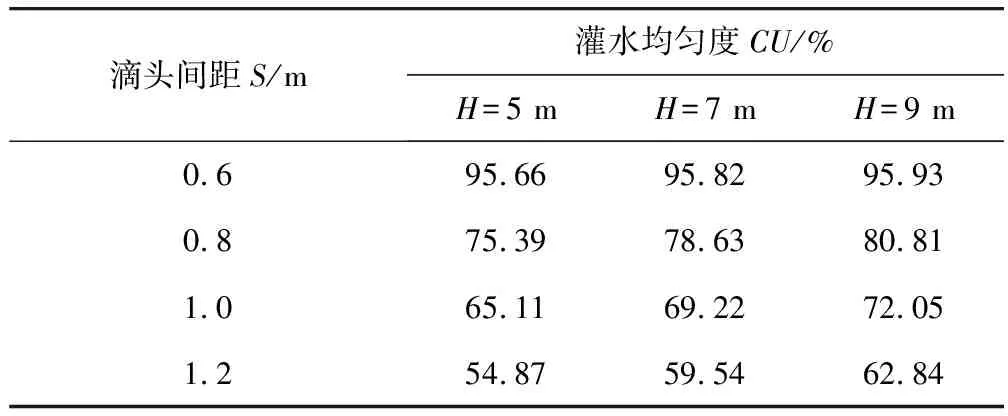
表1 滴头间距对出流均匀度影响
4 结 论
由上述试验结果及分析计算可得出如下结论:
1)大孔径薄壁出口与压力补偿式滴头的出流量试验表明,压力补偿式滴头优于大孔径薄壁出口,其出流均匀性得到了显著提高。由于其结构设计的合理性,将会使整个灌溉系统获得理想的灌溉均匀度;
2)不同管道长度试验表明:相同边界条件下,滴灌毛管长度越长,出流均匀性越弱。当工程要求长距离滴灌管道时,只有结合坡比、管径、滴头间距等参数的调整,使得出流均匀度满足要求;
3)不同初始水头的试验数据表明:在一定坡度条件下,初始水头越大,出流均匀度越高;
4)不同滴头间距的试验表明:长管道中滴头间距越大,出流均匀度越低。
由此可见,当设计灌水均匀度较低时,可通过减少毛管长度、增加初始水头、选择较大坡度和减小滴头间距等方法进行调整优化。针对具体工程时,当滴灌毛管长度、坡比等边界条件明确,可以适当增加初始水头、提高毛管管径、减小滴头间距等方法,以优化滴灌出流均匀度。
