基于岩电实验的储层岩石毛管压力与电阻率相关性分析
2022-04-09侯玢池崔鹏兴梁卫卫王小锋王起琮
侯玢池 崔鹏兴 梁卫卫 王小锋 王起琮
(1. 陕西延长石油(集团) 有限责任公司研究院, 陕西 西安 710065; 2. 陕西省特低渗透油气田勘探与开发工程技术研究中心,陕西西安 710065; 3. 中国地质大学(北京) 能源学院, 北京 100083; 4. 西安石油大学地球科学与工程学院, 陕西 西安 710065)
0 引 言
毛管压力是影响多孔介质中多相流体的重要参数之一, 通常采用压汞法、 半渗透隔板法和离心法等实验方法进行测定[1]。 对于低渗透、 非均质性强的复杂油藏, 毛管压力的实验方法测定难度很大, 且耗时费力; 此外, 从地层中取出的岩样很难维持原始的储层条件, 无法实时获得准确的毛管压力数据[2-4]。 相反, 电阻率数据可以通过测井等方法进行实时测量[5-7]。 在多孔介质中, 毛管压力、电阻率同为含水饱和度的函数, 从数学角度分析,由于这一共同特征, 两者应该存在某种函数关系,如果能找到这种关系, 就可以利用电阻率数据直接计算出毛管压力, 那将是非常有用的, 可以拓展传统电阻率测井在油藏工程中的应用。
关于毛管压力与电阻率之间关系的研究并不多。 M.T.Szabo[8]此前建立了一个毛管压力与电阻率指数之间的线性模型, 然而, 事实证明Szabo 模型在中低渗条件下并不成立。 D.G.Longeron 等[9]同时测定了储层条件下的毛管压力和电阻率指数,M.R.Dernaika 等[10]测定了混合润湿条件下碳酸盐岩储层岩石样品的毛管压力和电阻率指数, 但他们都未将这两个参数关联起来进行分析。 K.Li等[11-13]基于分形理论[14]和阿尔奇公式[15]建立了毛管压力和电阻率指数之间的幂函数关系模型, 但并未就模型中特征参数β值如何计算的问题进行说明。 故本文将以该模型作为理论基础, 基于毛管压力与电阻率联测实验结果, 针对β值开展进一步的分析研究, 从而在研究区内对现有的储层岩石毛管压力—电阻率数学模型进行验证与完善。
1 模型基础与存在问题
如前所述, K.Li 等[11-13]提出的毛管压力与电阻率幂函数模型可以表示为
式中:Snwi——非润湿相初始饱和度,%;Swr——润湿相残余饱和度,%。
为了利用实验数据验证式(3) 中的幂函数关系, K.Li 等[11-13]在室温条件下测量了某油藏位于不同地层(共14 块岩心) 的气水两相毛细管压力与电阻率数据。 实验过程中将岩心样品分为2 组(每一组各7 块岩心样品), 其中高渗组的渗透率为437×10-3~3 680×10-3μm2, 中低渗组渗透率为0.028×10-3~387×10-3μm2。 实验结果表明, 该模型对中低渗岩心数据的拟合效果优于高渗组[11]。
需要注意的是, K.Li 等[11-13]此前测试的所有岩石样品均来源于同一个油藏, 尽管渗透率范围很大, 但仍存在2 个问题:
(1) 式(2) 是否适用于其他类型油藏岩石样品;
(2) 如何确定式(2) 中的幂函数特征参数β值, 从而提高模型精度。
为了回答上述问题, 并且进一步验证Li等[11-13]提出的幂函数关系模型, 本次对出自X 油藏中2 口井的16 块岩石样品进行毛管压力和电阻率联测实验。 确定β值的思路是: 在研究过程中,探索利用其他已知参数或者可由实验手段测定的参数计算求出β值。 根据式(2), 一旦确定出β的值, 就可以直接计算出无因次毛管压力pcD, 从而建立一个精度更高、 适用性更强的储层岩石毛管压力—电阻率数学模型。
2 毛管压力与电阻率相关性的内在机理
利用毛管压力、 电阻率同为含水饱和度的函数这个基础, K.Li 等[11-13]推导出了两者之间的幂函数关系, 然而, 数学模型背后的物理机制仍需进一步探讨。 影响充液岩石电阻率的因素有很多, 包括孔隙喉道的大小、 形状、 分布和连通性等。 由于大多数岩石的基质都属于不良导电体, 电流主要通过孔隙空间内的流体进行传导, 充液孔隙空间的电阻率主要受孔隙结构和流体性质来控制[15]。 此外,有学者提出流体饱和度分布、 润湿性和温度对电阻率有重要影响[18-23]。 上述所有影响或控制充液孔隙空间电阻率的因素, 同样会影响毛管压力。 Man等[20]此前建立了一个预测油气藏岩石毛管压力和电阻率的三维孔隙网络模型。 结合特定岩石类型的孔隙结构几何性质, 如粒间孔隙形态和孔隙压缩性等, 在控制毛管压力和润湿性的条件下, 该模型能够很好地模拟孔隙尺度流体分布和电阻率。 模拟结果表明, 毛管压力可通过几乎相同的岩石和流体物理参数与电阻率关联在一起。 岩石的电学性质主要取决于所占据的孔隙空间的几何结构, 一方面, 电阻率主要受润湿相分布、 孔隙连通性、 迂曲度以及流体性质(盐度和温度) 的影响; 另一方面, 毛管压力主要受孔喉结构的影响, 但不受流体性质的影响。 因此, 可以认为电阻率与润湿相分布有关,而毛管压力则与岩石几何特征有关。 那么, 如何从电阻率推导出毛管压力呢? 实际上, 毛管压力也会受到润湿相分布的影响, 其中的一个证据是, 由于润湿相分布的不同, 驱替毛管压力通常不等于渗吸毛管压力; 同样的, 电阻率也会受到岩石几何特征的影响。 在式(2)、 式(3) 中, 利用电阻率指数来替代电阻率可以消除盐度、 温度以及其他流体性质对电阻率的影响, 电阻率指数不受这些参数的影响。
上述分析表明, 毛管压力和电阻率指数受相同的岩石、 流体物理参数控制, 两者之间存在一定的物理关系。 这一分析结果, 加之多孔介质中的毛管压力和电阻率都是润湿相饱和度的函数, 为用电阻率指数推导毛管压力提供了一定的理论依据。
3 联测实验
利用联测实验得到的电阻率和毛管压力数据结果, 对电阻率指数—含水饱和度的关系以及毛管压力—含水饱和度的关系进行分析, 并且将同一块岩样的毛管压力与电阻率指数进行数据拟合, 从而进一步分析两者之间的函数关系。
3.1 实验设计
3.1.1 实验样品
用于联测实验的16 块岩样均为砂岩天然岩心,分别来自X1 井和X2 井, 其长度为5.150 ~7.871 cm, 直径为2.547 ~2.589 cm, 孔隙度为17.62% ~30.70 %, 渗透率为9 × 10-3~974 ×10-3μm2。 X1 井取心样品所用模拟地层水矿化度为8 g/L, 密度为1.02 g/cm3。 X2 井取心岩样所用模拟地层水矿化度为7.5 g/L, 密度为1.02 g/cm3。
3.1.2 实验装置
在前人研究的基础上[24-28], 开发了一种基于半渗透隔板技术的新型毛管压力—电阻率联测实验装置(图1)。
整套实验装置主要由氮气瓶、 岩心夹持器(直径25 mm×长80 mm, 围压30 MPa)、 岩心、 隔板、 围压泵、 精密压力表(精度0.001 MPa)、 刻度管 (精度0.025 mL)、 电阻率仪 (QuadTech 1715 LCR Meter)、 计算机及数据自动采集系统(软件LabVIEW) 等设备仪器组建而成。
3.1.3 实验流程
实验之前先对岩心进行洗油和烘干, 之后模拟饱和地层水, 在确保实验装置气密性良好的条件下, 将岩心和半渗透隔板放入夹持器。 在同一压力条件下, 测量气水两相毛管压力、 电阻率以及含水饱和度数据(每块岩心不少于6 个压力点), 直到稳定状态。 实验结束后, 将岩心取出称质量, 计算出残余水饱和度。
本次研究区是油藏而非气藏, 为了尽可能的接近油藏实际条件, 应测定油水两相毛管压力而非气水两相。 一方面, 油水两相的半渗透隔板更为精密, 成本较高, 且操作复杂; 另一方面, 由于研究区储层岩石是强亲水的, 依照石油天然气行业标准SY/T 5346—2005 《岩石毛管压力曲线的测定》[29]中的规定, 当储层强亲水时, 可以使用气驱水毛管压力曲线来模拟油驱水过程的毛管压力曲线。 实验整体均在室温条件下进行, 实验数据及相关拟合结果见表1。
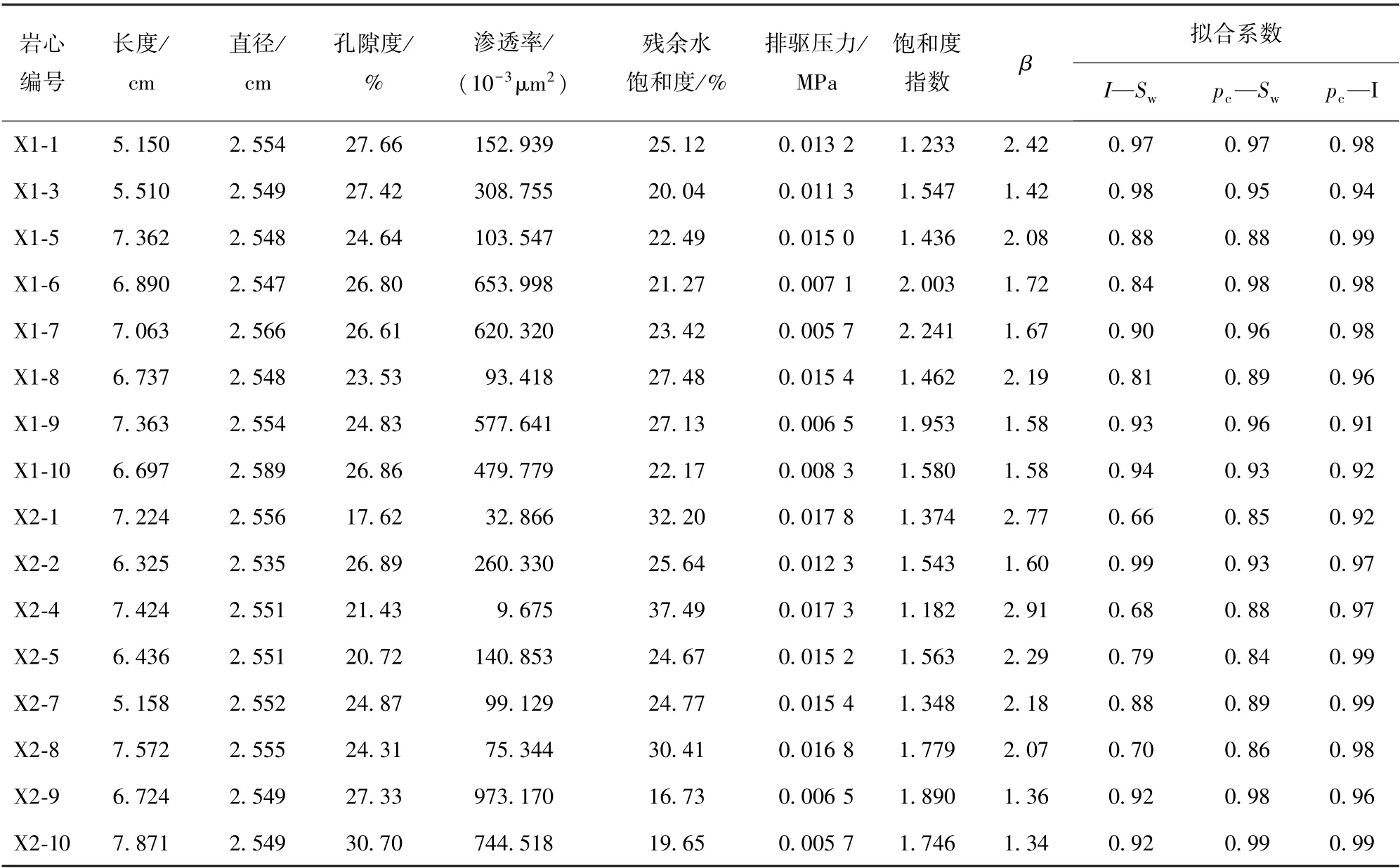
表1 岩心实验数据及拟合结果Table 1 Experimental data and fitting results of the core samples
3.2 实验结果分析
3.2.1 电阻率指数与含水饱和度相关性
对研究区岩心样品的电阻率指数—含水饱和度相关性进行分析, 以其中4 块岩心的数据拟合结果为例, 可以看出, 在双对数坐标下, 绝大部分数据点可以拟合成一条直线(图2), 即符合阿尔奇公式(式(3) ), 其中X1 井岩心的I—Sw拟合系数均大于0.84, X2 井岩心的I—Sw拟合系数大多大于0.8 (表1), 拟合度较好。 利用阿尔奇公式对数据点进行拟合, 可以得到各岩石样品的饱和度指数(表1), 饱和度指数范围为1.182 ~2.241, 平均为1.618。
由图2 可知, 在不同含水饱和度下测得的所有电阻率数据点基本上位于图中相对狭窄的区域内,所有岩石样品的电阻率与含水饱和度之间的关系均符合阿尔奇公式, 可以用于后续建立毛管压力与电阻率指数之间的关系。
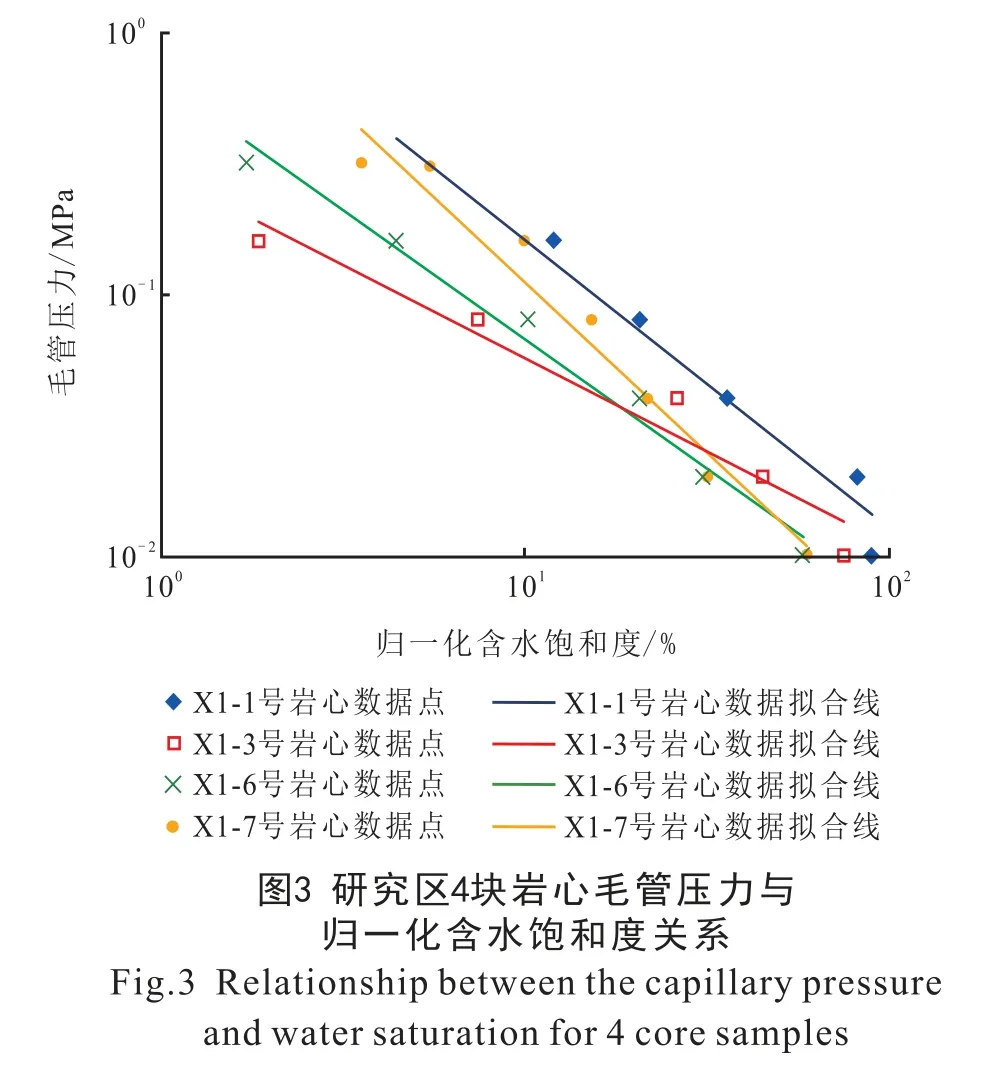
3.2.2 毛管压力与含水饱和度相关性

对研究区岩心样品的毛管压力—含水饱和度相关性进行分析, 以其中4 块岩心的数据拟合结果为例, 可以看出, 在双对数坐标下, 数据点均可以拟合成为一条直线(图3), 且拟合度较高,pc—Sw拟合系数R2基本保持在0.9 以上, 数据点均满足式(4) 中提到的Brooks-Corey 毛管压力模型。 利用Brooks-Corey 模型计算每块岩心的排驱压力(表1), 可以看出, 大部分岩心的排驱压力pe值为0.005 7~0.017 8 MPa, 平均为0.011 8 MPa, 岩心的渗透率越大, 排驱压力越低。
3.2.3 毛管压力与电阻率指数相关性
利用上述图2、 图3 中的联测实验数据, 可以得到同一块岩心毛管压力与电阻率指数之间的关系, 并用于验证公式(1) 以及公式(2) 中提到的幂函数关系模型(Li 模型)。 图4 (以其中4 块岩心的数据拟合结果为例) 显示了研究区岩心样品的毛管压力—电阻率指数关系, 可以看出, 在双对数坐标下, 利用同一块岩心样品测得的毛管压力与电阻率指数数据点可以拟合成为一条直线。 如表1所示,Pc—I拟合指数均大于0.9, 同时在岩心渗透率较低的条件下, 拟合效果更好。 因此, 图4中所显示的结果进一步验证了K.Li 和W.Williams先前所提出的毛管压力—电阻率指数幂函数模型。

4 模型修正
4.1 β 参数值确定
毛管压力与电阻率指数之间的拟合指数, 即幂函数模型特征参数β可以利用公式(2) 通过数据拟合得出, 结果如表1 所示, 对于大多数岩心,β最大值为2.91, 最小值为1.34, 平均值为1.95。
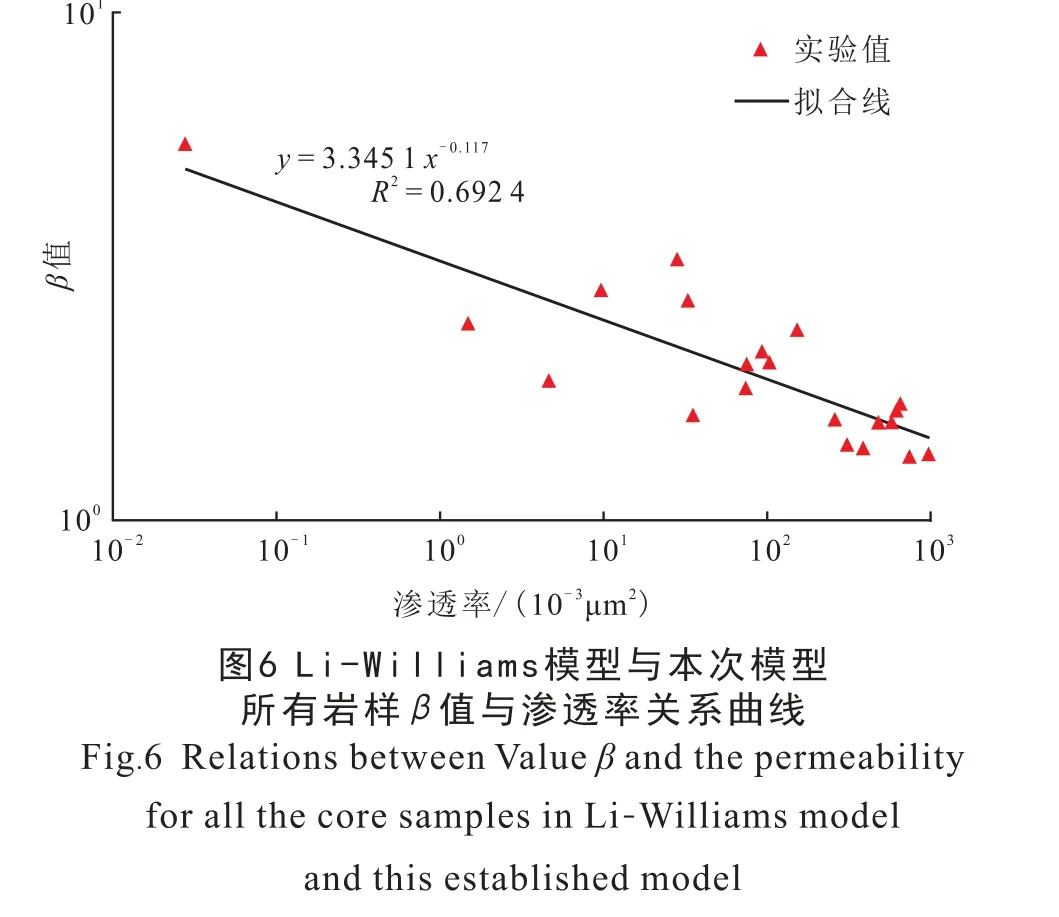
在初步确定β值的范围后, 应对其进行更为深入的数学分析。 由于β值无法直接获取, 因此需要借助其他已知参数或可通过实验手段测定的参数,经计算求得。 研究发现,岩心样品的β值与其渗透率K之间存在一定的关系。 如图5 所示。 对比分析K.Li 等先前的实验数据(中低渗岩心样品7 块)与本次研究的结果,可以看出,在双对数坐标下,β值和渗透率K的关系均可通过一条直线进行拟合,即β值随渗透率K的增加而减小, 拟合系数分别为0.699 9、 0.813 7。 综合K.Li 等的实验结果以及本次研究结果, 对全部岩样的渗透率K与β值之间的关系进行了拟合, 结果如图6 所示。 数据拟合度接近0.7。 由此便得到了3 组利用渗透率K计算β值的数学表达式, 即利用本次数据结果得到的


合并前后两次数据结果得到的
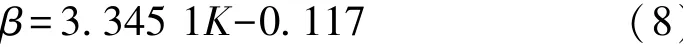
4.2 实际应用讨论
利用上述3 组β值数学表达式, 将其带入公式(1)、 (2) 中, 即可计算出对应的毛管压力pc值,对比毛管压力pc计算值与实验值, 分别求出3 组计算值、 实验值和标准差(表2), 可以看出, 利用 Li 模型数据结果得到的公式 ( 7),最终计算得到的毛管压力pc值与实验值之间的标准差最小, 即在本研究区内准确度相对更高, 本次β值拟合公式计算的结果次之, 合并样品数据β值拟合公式计算的结果标准偏差最大。 由此可以得出,利用公式(7) 可近似推导无因次毛管压力与电阻率指数之间的拟合指数β, 代入到公式(2) 的幂函数模型所得到的毛管压力pc值准确度较高, 从而在研究区内对K.Li 和W.Williams (2006 年) 提出的现有模型进行了一定程度的完善与修正。
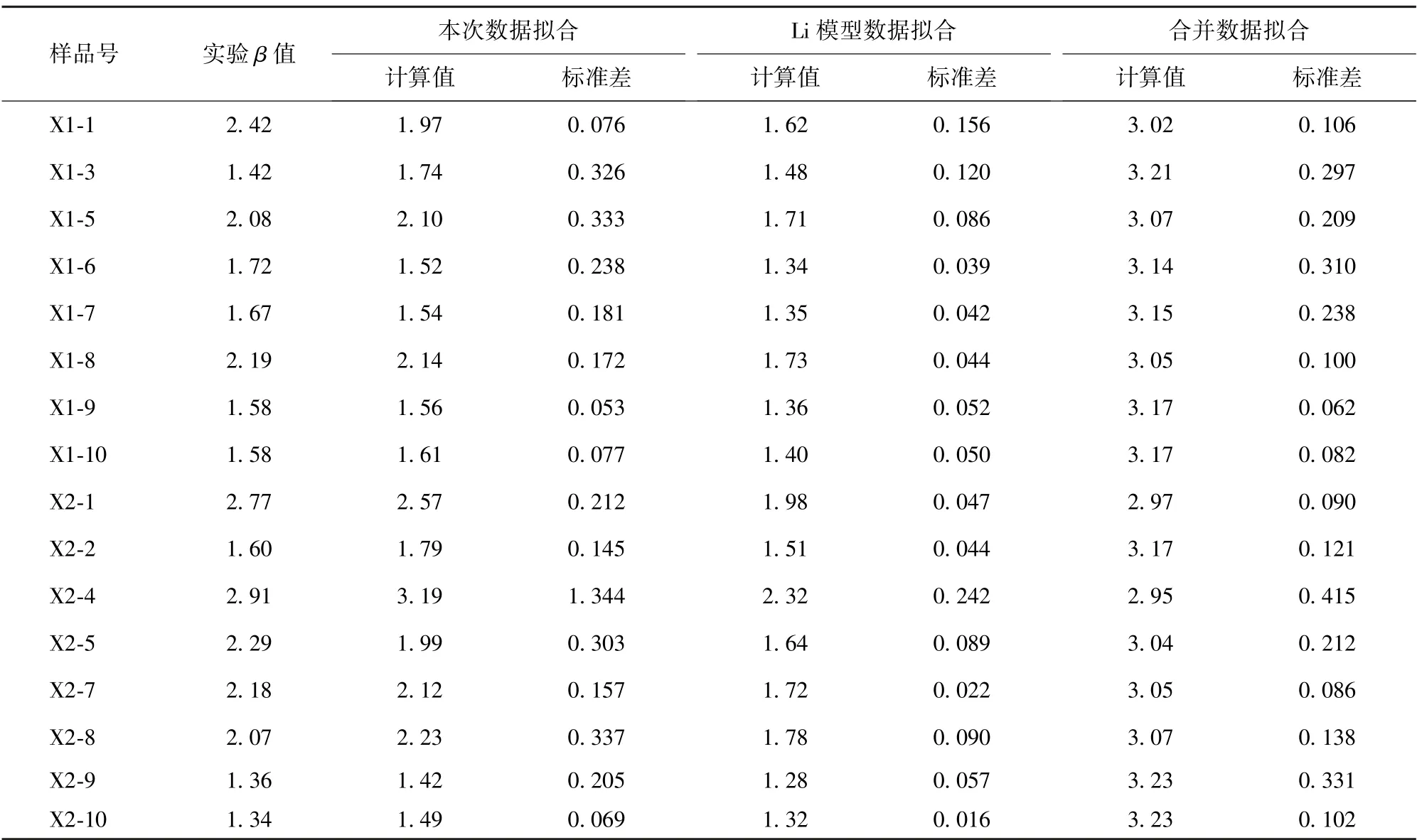
表2 三种方法计算的毛管压力值与实验值的标准偏差Table 2 Calculated capillary pressures by three methods and the standard deviations of the testing values
需要讨论的是, 3 组利用渗透率K计算β值的数学表达式中, 为何利用前人数据结果得到的表达式最终求出的毛管压力pc准确度最高, 这里对其中原因作一个定性分析。 笔者认为, 利用渗透率K求出β值, 并代入到公式(2) 的幂函数模型中,是对现有模型的完善, 即对于利用电阻率数据计算储层岩石毛管压力的最终模型, 渗透率K的重要性十分明显, 而前人数据结果中岩心渗透率K的取值范围更广(0.028×10-3~387×10-3μm), 更偏向于中低渗透率储层, 其适用性更强。 因此, 相较于本次数据结果得到的β值数学表达式, 其在该研究区内应用的准确度较高。
5 结 论
(1) 基于对毛管压力和电阻率指数之间幂函数模型(Li 模型) 的验证与进一步分析, 研究区岩石样品的特征参数β值与渗透率之间存在一定函数关系, 即β值随岩石渗透率K的增大而减小; 通过数据拟合, 可得到岩样β值范围为1.34 ~2.91, 平均值为1.95。
(2) 通过数据回归提出了确定毛管压力与电阻率指数之间特征参数β值的3 个数学表达式, 并对比毛管压力计算值与实验值之间的标准差, 确定出利用前人数据结果得到的表达式计算得到的毛管压力值准确度更高。
