预应力混凝土梁桥挠度监测的温度效应分离方法
2020-08-24吴海军
吴海军,何 立,韦 跃
(1.重庆交通大学 土木工程学院,重庆 400074;2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074;3.江苏交科交通设计研究院有限公司,江苏 南京 223001)
0 引 言
梁桥跨中下挠成为其跨径发展的瓶颈,是工程中面临急需解决的难题,同时也是桥梁健康监测中重点检测指标。对大跨径梁桥,由温度产生的挠度是桥梁长期变形及应力重分布的一个重要而复杂的影响因素,且在总挠度响应中占比较大,往往导致工程界所关心的活载效应信息被掩盖,干扰了对有用信息提取,影响了对结构的安全评估。因此,有必要研究温度效应对桥梁结构挠度造成影响的规律,并从总挠度值中剔除温度影响值,以此判断活载效应是否危及到桥梁结构安全,从而为桥梁健康监测预警阈值设置及进一步安全性评估提供依据[1-2]。
温度效应分离是采用统计回归等思想分析实际结构在监测状态下温度与挠度之间的变化规律,并根据该规律拟合函数方程,再由结构实测总响应值减去函数拟合预测值,从而实现温度效应的分离。目前,一些学者提出采用主成分分析、本征正交分解等方法来消除温度效应问题[3-4];有学者提出采用统计方法来消除温度效应对结构安全评估影响[5-6];有学者提出利用监测信号的多尺度特性,并结合小波分析[7]或粒子群优化算法[8]来对挠度温度效应进行分离;还有学者采用神经网络方法进行温度效应分离[9]。
前述各种温度效应分离方法均存在一定局限性,有的精度不够,不能满足工程要求;有的方法复杂,不易运用于工程实践。而在工程界中,往往需求的是一种既能符合工程要求,又简单易行的挠度温度效应分离实用方法。笔者采用的挠度温度效应分离法是将各种温度作用作为自变量,测点挠度值作为响应变量,运用桥梁结构响应值(位移、应变等)与整体升降温t0和截面温差Δt成线性的关系[10],建立线性回归模型,利用拟合函数方程计算出温度效应值,最后从实测总挠度中分离出温度产生的挠度效应。该方法理论简单,容易实现,且精度较高,可应用于桥梁结构的安全监测评估中。
1 实用方法相关理论
1.1 结构监测挠度值构成分析
由桥梁结构分析[11]可知,在某一时刻,混凝土桥梁结构任意一点的挠度I由以下几部分组成,如式(1):
I=IT+IP+IL+IR
(1)
式中:IT为由日照温度作用对桥梁产生的挠度变化值;IP为荷载(活载和恒载)使桥梁产生的挠度变化值;IL为桥梁结构长期挠度值,包括预应力损失、结构损伤及混凝土收缩徐变等所引起的挠度变化;IR为检测系统测试误差所引起的挠度误差值。
实际情况中,恒载引起结构的挠度可视为定值,不会随时间而发生改变(或其改变值可忽略不计);而活载对结构产生的挠度值为变量,呈现出随机性,无规律可寻,不易获取;通常桥梁健康监测系统都是在桥梁建成通车多年后才进行安装并工作的,而此时实桥的收缩、徐变等已基本完成,即可认为IL为常量。在扣除恒载及收缩、徐变等这些定值情况下,可发现桥梁挠度是温度作用与活载效应的耦合;温度对桥梁影响具有全局性且作用时间较长,活载影响主要是以暂时性为主,作用时间短;故温度作用是桥梁挠度监测中最主要影响因素,对桥梁健康监测有用信息提取产生了较大干扰,这就决定了分离桥梁挠度中的温度效应是有必要且有意义的。
1.2 多元线性回归模型简介
多元线性回归模型[12]表达的是多个自变量与响应变量之间关系函数。令Y为响应变量,X1,X2, …,XP为表达Y的P个互异自变量,规定X1=1,则有多远线性回归模型,如式(2):
Yi=β1+β2X2i+…+βpXpi+μi
(i=1,2,…,n)
(2)
式中:μi(i=1, 2, …,n)为随机扰动项;β1,β2, …,βP分别为回归系数。
1.3 多元线性回归模型检验方法
1.3.1 拟合优度检验(R2检验)
R2检验是用来评价线性回归模型优劣程度的参数,可通过S回与S总比值来判断相关性程度,其比值越大,模型相关性越高;反之,相关性低。如式(3):
(3)
式中:S总为各样本值与样本平均值之差的平方和,称之为总离差平方和;S残为样本中未被模型包含部分对总体所产生的影响,称之为残差平方和;S回为样本中被模型包含部分对总体产生的影响,称之为回归平法和。
1.3.2 方程显著性检验(F检验)
F检验用来判断模型是否具有显著的线性关系。应用数理统计理论如式(4):
(4)
统计量F服从以(p,n-p-1)为自由度的F分布。在实际应用计算时,应先计算出统计量F,然后根据已知的显著性水平系数进行判断,若F>F(p,n-p-1),可判定为线性关系显著;若F 对于大跨径梁桥,挠度是桥梁结构进行施工监控、荷载试验及运营期间健康监测的一项重要检测指标[13-14]。温度效应对结构挠度监测产生的影响较大,掩盖了活载作用对桥梁挠度产生的影响,而活载作用产生的挠度恰是人们所关心的,不容忽视。 根据相关理论,笔者提出了分离桥梁挠度监测中温度效应的一种实用方法。利用该方法提取活载效应信息,以此对桥梁安全及使用寿命提供保障;并以江津长江大桥为依托,运用此方法对桥梁挠度中的温度效应进行分离。 根据上述理论分析,可归纳出分离温度效应方法的操作步骤为:① 布置测点,采集数据;② 对采集数据进行分析,建立温度与挠度关系曲线,通过对比,初定有效测点;③ 构建线性模型并依照以上相关理论计算回归参数;④ 根据回归参数确定出最佳模型,并以此拟合温度和挠度关系的回归直线方程;⑤ 从实测总挠度值中扣除由回归方程得到的拟合值即可实现对温度效应分离。 重庆江津长江公路大桥于1997年建成并投入使用,主桥为三跨连续刚构桥,桥跨布置为140 m+240 m+140 m,全长520 m,主梁采用单箱单室截面。此桥跨中曾经下挠严重,通过对该桥采用增设体外预应力方法进行加固,成功地提高了该桥的承载能力和结构刚度,抑制了主跨跨中的下挠趋势,改善了主梁应力状况,桥梁线形有了明显改善。为保证该桥在运营期间安全可靠,在2011年对此桥设置了成套健康监测系统。 针对该桥的挠度监测,在主跨跨中、1/4截面处安装点激光器,在主跨两侧墩处各安装1个投影标靶。安装位置详见图1、2。 针对该桥温度监测,在主跨德感侧墩箱梁上安装3个温度传感器,分别为WD1-上游侧箱梁外、WD2-下游侧箱梁外和WD3-箱梁内。安装位置详见图3、4。 为了研究主梁跨中挠度值受温度变化影响规律,笔者提取了自2011-12-26—2013-09-25以来,连续21个月内主梁跨中挠度数据与1~3测点实测温度数据,并绘制了相应的时程曲线,如图5、6。横坐标“监测时间点”指监测指标数据值提取次数。 由图5可发现:测点1~3的温度时程曲线变化规律大致相似,这反映出温度对箱梁内部和外侧影响总体一致。另外,测点1、2的波动起伏相对较大,而测点3波动变化相对平缓,这主要是因为测点1、2布置于箱梁外侧,而测点3布置在箱梁内部,箱梁外侧受日照辐射影响较箱内更为敏感、直接,故箱梁外侧测点时程曲线波动情况不同于箱梁内部。 由图6可看出:跨中测点挠度曲线与箱内测点3的温度值时程曲线走势基本相同,表现为:温度低、挠度小;温度高、挠度大的变化特征,体现出了测点3温度值与跨中测点挠度值有着较强的正相关性。 根据以上述叙可知:跨中挠度变化与温度变化关系呈正相关性;测点3时程曲线与实测挠度时程曲线波动趋势较测点1、2更贴近,即说明测点3温度变化与跨中挠度变化的正相关性更显著。 为使各测点的温度值与跨中挠度值关系更加明确,以便初步判断出有效测点,笔者绘制了各测点的温度与挠度相关图,如图7。由图7可知:各测点温度值与跨中挠度值的关系曲线均呈现出了比较明显的线性关系,可近似用斜直线方程来模拟取代。通过对比发现:跨中挠度值与测点1、2温度值的离散程度较测点3大,也可认为测点3的温度值与跨中挠度值线性相关性优于测点1、2。由此可初步断定测点3为分离挠度中温度效应的有效测点,但此结论只是定性判定,其结果并不具有说服力。各测点温度值与跨中挠度值之间线性关系是否显著需经回归参数来定量判断。 笔者通过建立4种线性回归模型,并依据以上相关理论基础,利用MATLAB进行计算,得到了相应的回归参数值,如表1。 表1 4种温度-挠度线性回归模型参数 由表1可见,模型1、2的回归参数基本一致。其中,模型1相关性判定系数R2=0.480;模型2的相关性判定系数R2=0.478,这表明了模型1、2相关性均较差。模型3、4相关性判定系数R2均为0.94,表明模型相关性较好;由此说明测点3温度值与跨中挠度值的正相关性要优于测点1、2,此结果也同上述初步分析判断结论相吻合。根据模型3的F检验结果,F=2 086.923>F0.05(1,1338)=3.85,相应的P=0,满足P<0.05,可判断该模型线性关系显著;当然,模型4也满足条件,但不及模型3操作便捷;模型1、2的P=0,亦满足P<0.05,但其相关性较差,这使得F检验结果失效。 综上所述,测点3温度值与跨中挠度值存在强烈线性关系,可近似用斜直线进行拟合;用测点3温度值为自变量的一元线性回归模型拟合线性直线方程以分离温度效应是4种模型中效果最好的,且操作简单,便于实现。 以测点3温度值为自变量,跨中挠度值为因变量,进行拟合回归直线方程计算,从而实现挠度温度效应分离。图8为测点3的温度值-跨中挠度值相关性及拟合直线图。利用图8得到的线性回归直线方程计算出各温度作用下跨中对应的挠度值,并与实测挠度值进行对比,以便分析活载效应信息,如图9。 图9中:除个别点出现异常峰值外,其余的线性回归拟合值与实测挠度值基本接近;异常峰值可解释为数据采集错误或桥梁受到了突然冲击作用;在不考虑异常值情况下,用实测挠度值减去线性回归拟合值,即实现了对温度效应分离,其差值(残差)可视为是活载产生的挠度值,以此便可得到活载效应信息,以便对桥梁健康监测提供有利依据。 利用以上残差分析,可对桥梁安全运营做出实时监控及预警。根据结构满足正常使用极限状态为原则,设定预警界限值,若残差在预警界限值以内则可认为桥梁结构运营正常,处于安全适用状态;若残差超出预警界限值,则可认为桥梁超载或有突发情况发生,可能会危及到桥梁安全及使用寿命,此时应向桥梁运营管养部门发出警报信息,便于采取及时有效的对策,以防事故恶性发展。 笔者基于江津长江大桥工程背景,以各测点温度值作为自变量,跨中挠度值作为响应变量,建立线性回归模型,对实测总挠度中的挠度温度效应进行分离。根据分析,可得到以下结论: 1)通过建立模型,利用线性回归思想以分离桥梁挠度中温度效应方法,精度较高,方便操控,具有较强的实用性; 2)对于大跨径箱型截面梁桥,跨中挠度值与箱梁内部温度监测值的正相关性较箱梁外侧温度监测值更加显著,且跨中挠度与箱梁内部温度之间存在较强的线性关系; 3)从实测挠度值中减去挠度温度效应的线性回归拟合值,即实现了分离温度效应之目的,其差值一般可认为是活载产生的挠度值; 4)以正常使用状态为原则,利用残差,设置相应的预警界限值,可对桥梁的安全运营提供保障。2 实用方法操作
3 应用实例
3.1 工程概况
3.2 跨中挠度和各测点相关性分析
3.3 线性回归模型
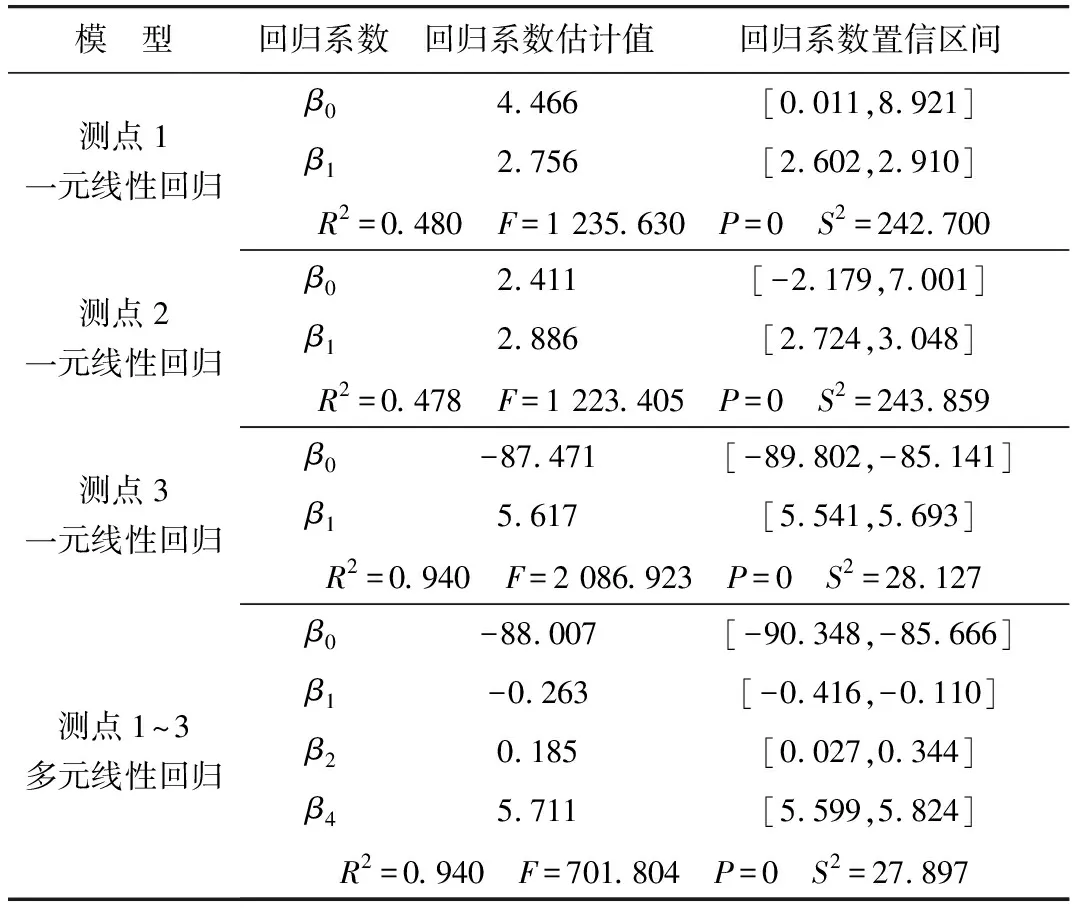
3.4 温度效应分离
4 结 论
