大庆长垣扶余致密油层YP井产量递减分析

徐国涵　尹洪军　邢翠巧

摘      要：大庆长垣扶余致密油层的YP井初期产量递减快，后期产量递减缓慢，常规产量递减分析方法已不再适用。基于致密油井生产动态特征分析，连续计算各类地层条件和边界条件下的致密油生产数据递减率，根据递减率所呈现的幂律行为建立幂律指数产量递减模型。对于模型中的初始产量、无穷递减率、初始递减率和递减指数进行敏感性分析。利用该幂律指数产量递减模型对YP井的产量进行分析，得到较好的拟合结果，并给出预测产量和最终累计产量。该方法为大庆长垣扶余致密油层油井产量递减分析提供了科学依据。

关  键  词：致密油井;递减率;产量递减分析;曲线拟合;产量预测

中图分类号：TE348       文献标识码： A       文章编号： 1671-0460（2020）07-1424-04

Analysis on Production Decline of Well YP in Fuyu Tight

Oil Layer of Daqing Changyuan Block

XU Guo-han1，2， YIN Hong-jun1，2， XING Cui-qiao1，2

（1. Department of Petroleum Engineering，Northeast Petroleum University， Daqing Heilongjiang 163318，China;

2. Key Laboratory of Enhanced Oil Recovery of Ministry of Education，

Northeast Petroleum University， Daqing Heilongjiang 163318，China）

Abstract： The initial production of tight oil well YP in Daqing Changyuan Fuyu tight oil layer decreased rapidly， and the production declined slowly in the later stage. The conventional production decline analysis method is not suitable. Based on the production characteristics of tight oil wells， the decline rate of tight oil production data were continuously calculated under various stratum conditions and boundary conditions， and a power law exponential production decline model was established based on the power law behavior presented by the decline rate， the method of power law exponential decline analysis was established. Sensitivity analysis was performed based on initial production， infinite decline rate， initial decline rate， and decline index in the established model. The power law exponential decline model was used to analyze the production of tight oil well YP， and the good matching results were obtained. The production forecast and final cumulative production were carried out. This method provides a scientific basis for the analysis of the production decline of the oil wells in the Fuyu tight reservoir of Daqing Changyuan block.

Key words： Tight oil well; Decline rate; Production decline analysis; Curve matching; Production prediction

大慶长垣扶余储油层具有渗透率超低的特征，该油层油井生产动态具有“两段式”特征，初期产量高、递减率大，中后期产量低、递减率减缓^[1-3]。由于致密油复杂的生产动态特征，常规产量递减分析方法已不适用。致密油生产动态特征分析和产量预测是当前储量评价工作的难点之一^[4?5]，因此，建立适用于大庆长垣扶余致密油层的YP致密油井的产量递减分析方法对于该区油藏开发具有重大意义。

1908年，Arnold和Anderson最早提出递减曲线分析（DCA），他们认为任何时候的产量都是前一时刻产量的函数。只需要提供生产数据，不需要储层信息，能较快的对油藏进行评价^[6]。1920年，Johnson等^[7]通过对生产动态资料的研究提出了递减率和递减率导数的概念，为产量递减分析打下基础。1945年，Arps等^[8]提出了递减曲线分析方法，但其要求的客观条件相对苛刻。2008年，Ilk D^[9-10]等提出了幂律指数产量递减分析方法，并通过实例验证该方法的正确性。2013年，段永刚等^[11]引入了幂律指数产量递减分析方法，并验证了该模型对于非常规油气资源的适用性。常规产量递减分析方法只能用于拟稳定流阶段生产阶段，致密油井不稳定生产时间长，很难到达拟稳定流，利用该方法对致密油井进行产量预测和储量预测时会出现较大偏差，而幂律指数产量递减分析方法可用于分析致密油井不稳定流、过渡流以及边界流等生产阶段。

通过对大庆长垣扶余致密油层的YP井的生产数据分析，发现其生产动态曲线在前期成指数形式下降，时间持续半年左右，此阶段产量递减率最大;随着时间的推移，后期产量趋于平稳，无较大波动，处于低产稳产的状态。在前人研究的基础上^[12-14]，基于致密油生产动态特征，采用幂律指数产量递减分析方法。考虑递减指数和无穷递减率的影响，绘制幂律指数产量递减无因次图版，并进行参数敏感性分析。对大庆长垣扶余致密油层的YP致密油井产量进行了递减分析，得到了较好的拟合结果，并对该井产量进行了预测，为大庆长垣扶余致密油层油井产量递减分析提供了科学依据。

1  幂律指数产量递减模型

递减率是指单位时间内产量的变化率，用来反映油气井产量递减的快慢程度，即单位时间内产量递减百分数，通常用D表示：

           （1）

式中：D — 递减率，d^-1;

q — 油气井产量，m³·d^-1;

t — 生产时间，d。

利用商业软件Topaze模拟出不同地层、不同边界条件下致密油井产量递减曲线，连续计算出不同模型的递减率D并绘制了lgD-lgt图，如图1所示。发现递减率曲线呈现幂律行为，即曲线在双对数图上呈直线趋势。曲线后期有下掉趋势，说明此时曲线递减率减小，产量递减速度减缓。

基于对D參数的幂律行为的观察，使用幂律函数对递减率进行建模。其表达式为：

（2）

进一步考虑致密油井随着生产时间延长，产量递减减缓、递减率降低等特点，引入新参数无穷递减率D_∞，重新定义递减率D为：

（3）

式中：D_∞ — 当时间趋于无穷大时的递减率，d^-1;

D₁ — 当生产时间为1天时的递减率，d^-1;

n — 递减指数，取值在0～1之间，无因次。

式（3）的物理意义为生产时间较短时，幂律项为递减模型主要影响因素，递减率可由递减的幂律递减率来近似;而当生产时间逐渐增加趋于无穷大时，幂律项对于递减模型的影响逐渐变小，递减率会趋于无穷递减率D_∞。

将式（3）代入式（1）进行整理得到幂律指数产量递减模型：

（4）

式中： _i — 常数， _i=D₁/n，d^-1。

式（4）说明在生产早期阶段，产量特征由D₁/n控制;在生产晚期阶段，即生产达到拟稳态或边界控制阶段，产量主要由D_∞控制。

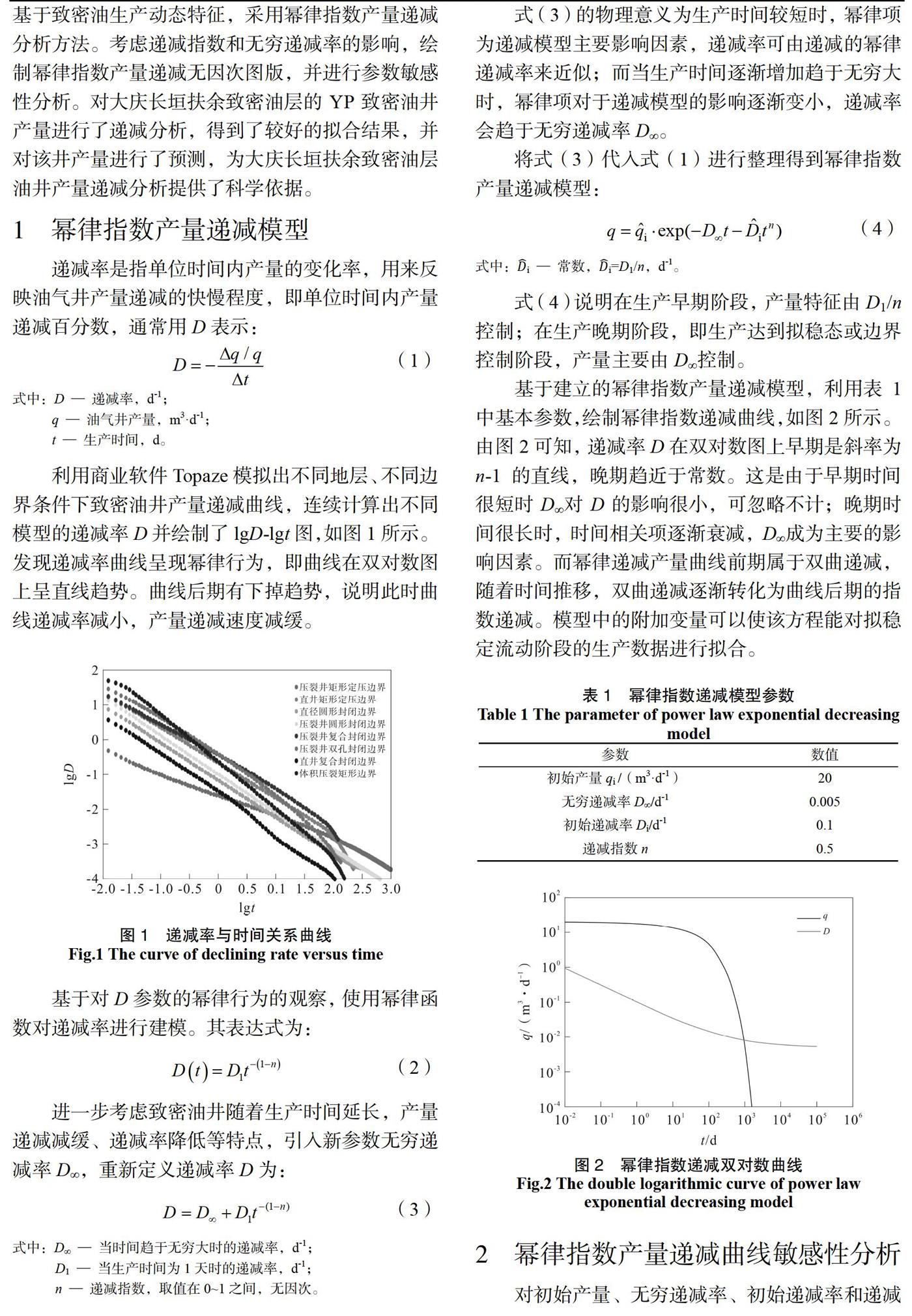
基于建立的幂律指数产量递减模型，利用表1中基本参数，绘制幂律指数递减曲线，如图2所示。由图2可知，递减率D在双对数图上早期是斜率为n-1的直线，晚期趋近于常数。这是由于早期时间很短时D_∞对D的影响很小，可忽略不计;晚期时间很长时，时间相关项逐渐衰减，D_∞成为主要的影响因素。而幂律递减产量曲线前期属于双曲递减，随着时间推移，双曲递减逐渐转化为曲线后期的指数递减。模型中的附加变量可以使该方程能对拟稳定流动阶段的生产数据进行拟合。

2  幂律指数产量递减曲线敏感性分析

对初始产量、无穷递减率、初始递减率和递减指数进行敏感性分析，说明了每个参数对产量曲线形态的影响。曲线绘制时选用的坐标有所不同，除直角坐标外还有半对数坐标和双对数坐标，充分说明了不同参数对产量曲线特征的影响。

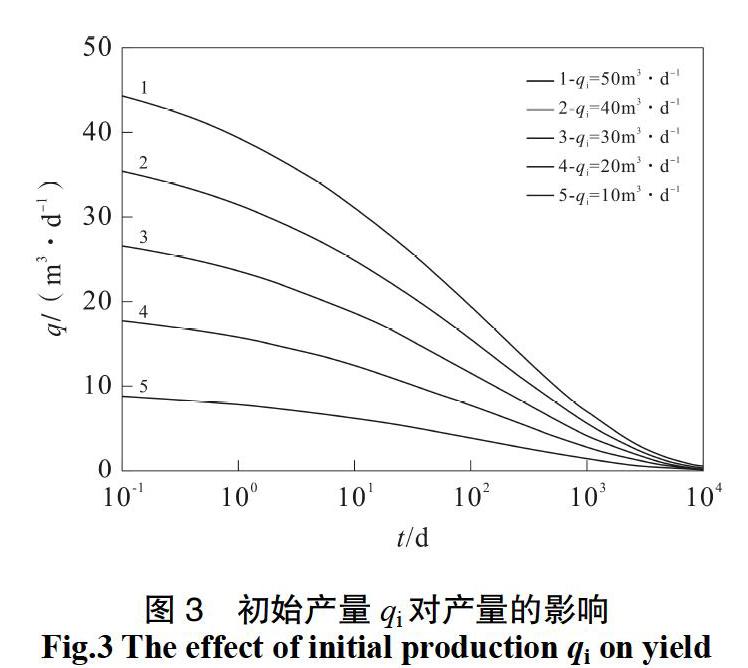
初始产量q_i对半对数坐标下产量-时间曲线的影响，如图3所示。q_i控制整条曲线上下移动，但不同的q_i对应的曲线只在前期起伏明显，随着时间的推移，后期的曲线起伏变化不大。

无穷递减率D_∞对双对数坐标下产量-时间曲线的影响，如图4所示。D_∞控制的是在lgq-lgt双对数坐标轴上曲线随时间推移靠近横轴的快慢程度，D_∞越大，曲线靠近横轴的趋势出现得越早;D_∞越小，曲线靠近横轴的趋势出现得越晚。D_∞的取值对曲线前期影响不大。

初始递减率D_i对半对数坐标下产量-时间曲线的影响，如图5所示。通过分析可得D_i控制曲线前期的递减快慢，D_i越大，曲线在前期递减的程度越大。另外D_i还控制曲线后期靠近横轴的快慢，D_i越大，曲线在后期靠近横轴的时间越快。

递减指数n对直角坐标下产量-时间曲线的影响，如图6所示。递减指数n控制曲线前期的凹凸程度，n越大曲线越向内凹，曲线递减程度越大;反之，n越小曲线向内凹的程度越小，曲线递减程度越小。

3  YP井产量递减分析

YP井是大庆长垣扶余致密油层一口体积压裂水平井。该井原始地层压力16.9 MPa，产层厚度2.0 m，孔隙度0.126，渗透率1.02 mD。该井于2014年4月投产总共历时54个月，利用幂律指数递减模型对该井的生产动态数据进行拟合分析，得到参数见表1，拟合曲线如图7所示。

产量递减方程为：

q=53.28exp（-0.000 1t-0.249 8t^0.297）  （5）

从图7可以看出，幂律指数产量递减模型可以较好地拟合YP井的生产数据，理论产量曲线基本与实测产量趋势一致，累计产量预测曲线与实际累计产量曲线基本重合。

递减率为：

D=0.000 1+0.071 2t^-0.715      （6）

根据幂律指数产量递减模型可对该井进行产量预测，当产量降至3 t·d^-1时，经历时间为9.3年，累计产量G_p为25 102.4 t;当产量降至1 t·d^-1时，经历时间为21.2年，累计产量G_p为32 712.3 t;当致密油井生产50年时，产量q降为0.143 t·d^-1，累计产量G_p为37 154.1 t;当致密油井生产100年时，产量q降为9.44×10^-3 t·d^-1，累计产量G_p为38 022.1 t。最终累计产量为38 092.3 t。

4  结论

1）幂律指数递减模型可用于分析稳态流、非稳态流和边界控制流，能较为准确的预测致密油井产量和累积产量，并能计算出最终累计产量，适用于致密油井产量递减分析。

2）产量递减曲线在前期近似为一条平行于横轴的直线，说明致密油产量递减迅速。随着时间的推移，曲线逐渐过渡成为一条垂线，越早偏向水平线说明递减指数越大，油井开采时间越短。

3）利用幂律指数产量递减模型对YP井进行了产量递减分析，较好的拟合了该致密油井生产数据和累积产量数据，获得了产量递减率和产量递减方程，并计算出该井的最终累计产量，为大庆长垣扶余储油层油井产量递减分析提供了一种有效方法。

参考文献：

[1]徐立研， 王胡振， 张立韧， 等. 中国致密油研究现状及发展趋势[J]. 当代化工， 2017， 46 （01）： 86-88.

[2]高岩冰. 大庆长垣扶余油层成藏特征及勘探潜力[J]. 石化技术， 2018， 25 （09）： 126.

[3]闫文华， 赵玉双， 王洪岩，等. 大庆长垣外围油田产量递减因素分析及控制对策[J]. 石油地质与工程， 2007 （05）： 62-64.

[4]尹洪军， 杨春城， 唐鹏飞， 等. 大庆长垣YP1超长水平井分段压裂优化设计[J]. 特种油气藏， 2014， 21 （05）： 68-71.

[5]国强. 致密油藏渗流机理分析及开发方式探讨[J]. 中国石油和化工标准与质量， 2018， 38 （13）： 94-95.

[6]ARNOLD R，ANDERSON R. Preliminary report on coalinga oil district， fresno and kings counties[R]. U.S. Geological Survey Bulletin; US Government Printing Office： Washington， DC， USA， 1908.

[7]JOHNSON R H， BOLLENS A L. The loss ratio method of extrapolating oil well decline curves[J]. Trans. AIME， 1927， 77 （1）： 771-778.

[8]ASPS J J. Analysis of decline curves. Transactions of the american institute of mining[J]. Metallurgical and Petroleum Engineers， 1945， 160： 228-247.

[9]ILK D， RUSHING J， PEREGO A， et al. Exponential vs. hyperbolic decline in tight gas sands： understanding the origin and implications for reserve estimates using Arps decline curves[C]. SPE 116731， 2008.

[10]ILK D， CURRIE S， SYMMONS D， et al. Hybrid rate-decline models for the analysis of production performance in unconventional reservoirs[C]. SPE 135616， 2010.

[11]段永刚， 曹廷宽， 王容， 等. 页岩气产量幂律指数递减分析[J]. 西南石油大学学报（自然科学版）， 2013， 35 （05）： 172-176.

[12]白玉湖， 杨皓， 陈桂华， 等. 页岩气产量递减典型曲线中关键参数的确定方法[J]. 特种油气藏， 2013， 20 （02）： 65-68.

[13]曹安， 曹国娟， 张旭， 等. 用幂率指数产量递减方程预测非常规气藏可采储量[J]. 辽宁化工， 2015， 44 （03）： 315-317.

[14]齐亚东， 王军磊， 庞正炼， 等. 非常规油气井产量递减规律分析新模型[J]. 中國矿业大学学报， 2016， 45 （04）： 772-778.

基金项目：国家科技重大专项，致密油体积压裂试井方法研究（项目编号：2017ZX05071005）。

收稿日期： 2019-10-13

作者简介：徐国涵（1995-），男，河北省沧州市人，硕士研究生，研究方向：油气渗流理论与应用。E-mail：1219973727@qq.com。