降低DCO-OFDM系统峰均功率比的IGA-SLM算法

李天屿,李蔚泽,洪文昕,陈建飞

(南京邮电大学 a.通信与信息工程学院; b.电子与光学工程、微电子学院,南京 210023)

0 引 言

正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术是一种高效的多载波通信方案,在可见光通信(Visible Light Communication,VLC)研究中备受瞩目[1]。VLC采用强度调制直接检测系统,要求输入信号是单极性信号和实值传输,但传统射频OFDM技术无法满足信号要求。对此,文献[2-3]提出直流偏置光-正交频分复用(Direct Current-biased Optical OFDM,DCOOFDM)方案,该方案可以有效地解决上述问题。

在DCO-OFDM系统中,信号的峰均功率比(Peak to Average Power Ratio,PAPR)较高。目前,PAPR抑制技术主要有以下3类[4]:畸变类、编码类和概率类方法。在概率类方法中,选择性映射(Selected Mapping,SLM)算法因其良好的PAPR抑制性能而备受关注。但SLM算法因其本身的局限只能获得系统的局部最优解,对此,本文提出一种改进型遗传选择性映射算法(Improved Genetic Algorithm Selected Mapping,IGA-SLM),其利用改进型遗传算法来高效搜索系统中的全局最优解,从而更进一步地降低了VLC DCO-OFDM系统的PAPR。

1 基本原理

1.1 VLC DCO-OFDM系统及PAPR定义

图1所示为VLC DCO-OFDM系统的发送端模型。二进制数据通过M点正交振幅调制(M-Quadrature Amplitude Modulation,MQAM)、串/并变换后,经Hermitian对称[5]输出实值信号。完成Hermitian对称的信号经N点快速傅立叶逆变换(N-Inverse Fast Fourier Transform,N-IFFT)运算后得到DCO-OFDM信号,该信号往往具有较高的PAPR。信号x(t)的峰值功率与平均功率之比可定义为

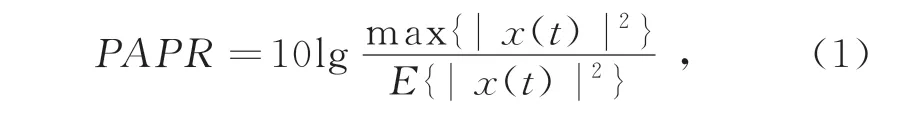
式中:t为时间；E{}为数学期望。此后DCOOFDM信号完成并/串变换、加循环前缀(Cyclic Prefix,CP)、直流(Direct Current,DC)偏置、通过滤波器(Filter)、数模变换(D/A conversion,D/A)等过程,最终由发光二极管(Light Emitting Diode,LED)将调制后的光信号发送至信道中。

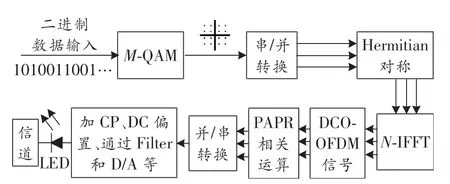
图1 VLC DCO-OFDM系统发送端模型

1.2 SLM

SLM的主要思想是:将上述完成的Hermitian对称信号与随机生成的有限组相位旋转序列相乘得到备选信号,所有备选信号通过N-IFFT后形成备选SLM信号,挑选其中PAPR最小的SLM信号进行发送,同时发送包含相位旋转序列信息的边信息[6-7]。

可见,传统SLM算法只能从有限组相位旋转序列中寻找出局部最优的相位旋转序列,无法找到全局最优序列。智能优化算法可以高效解决此类最优解问题,遗传算法就是一种典型的智能优化算法。

2 IGA-SLM设计

2.1 遗传SLM算法

遗传算法最早由Holland教授提出,是一种基于基因遗传学原理和自然选择的高效智能算法[8]。该算法在实际应用中将染色体序列看作实际问题的解,将种群看作实际问题的解空间。种群通过遗传运算更新迭代,包括选择、染色体序列交叉和变异等过程。此后评估新一代解空间的适应度,适应度较差的解将被逐渐淘汰,适应度较好的解则等待下一次遗传更新迭代,其中适应度指实际问题的目标函数。随着算法的不断迭代,最终逐步高效地搜索出实际问题的最优解[9-10]。

结合遗传算法和SLM算法的特点,提出遗传SLM算法(Genetic Algorithm-SLM,GA-SLM)。在实际中,SLM算法的相位旋转序列代表GASLM的染色体序列；相位旋转序列的交叉和变异代表GA-SLM的染色体交叉和变异；DCO-OFDM系统的PAPR性能代表GA-SLM的适应度,GA-SLM的适应度函数表示为

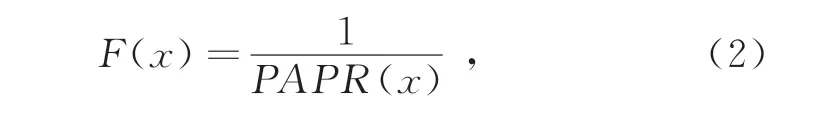
式中,PAPR(x)为信号x的PAPR值。GA-SLM的主要参数有:DCO-OFDM系统的子载波数,子载波数决定了相位旋转序列的长度；迭代次数,指遗传更新迭代的次数；相位旋转序列交叉概率和变异概率,指遗传更新迭代中相位旋转序列成功交叉和变异的概率,二者分别影响着解空间的进化速度和多样性。

2.2 IGA-SLM

虽然GA-SLM具有优秀的寻优能力,但在搜索全局最优解的过程中容易陷入“早熟问题”,即发生过早收敛[11]。对此,本文提出以下几个改进措施:

(1)自适应调整机制:引入自适应系数β(β＞1)和差异系数γ(γ＞1)。若解空间中的最佳PAPR与平均PAPR的差值低于后者的γ倍,意味着解空间中的解逐渐趋于相同,即将出现收敛,因此扩大变异概率β倍以增加解空间的多样性,同时交叉概率缩小到原来的1/β用以减缓解空间的进化速度；反之,若二者的差值不低于平均PAPR的γ倍,则将变异概率降低到原来的1/β并扩大交叉概率β倍。同时,交叉概率和变异概率不可能无限地增大或减小,因此还需对调整区间做出规定。

(2)自适应多点交叉机制:在相位旋转序列的交叉过程中一般仅有一个交叉点,两个序列通过该交叉点完成一次交叉过程,如图2(a)所示。因为序列一般较长,因此单点交叉往往会对序列造成较大改变,性能较好的序列可能因此造成严重退化。文献[9]提出的多点交叉可以在避免序列大幅改变的同时,保证新序列较上一代有明显不同,如图2(b)所示。在此基础上本文提出自适应多点交叉机制,当解空间中即将出现收敛时,自动减少交叉点数以增加序列变化幅度；反之则增加交叉点数。这里也需要对自适应交叉点数的调整区间做出规定。

(3)最优解保护机制:评估解空间的PAPR性能之后,为避免当代最优相位旋转序列因某些不合适的遗传运算而发生退化,故将其直接保留至下一代,即跳过遗传运算。

(4)立即淘汰机制:引入立即淘汰率α(α＞1),对PAPR值超过平均PAPR值α倍的相位旋转序列采取跳过自然选择的方式进行立即淘汰处理,并随机产生同等数量的新序列立即加入解空间,新序列将继承被淘汰序列的遗传能力以完成后续的遗传运算。

到此,我们将基于以上改进措施的GA-SLM称为IGA-SLM。

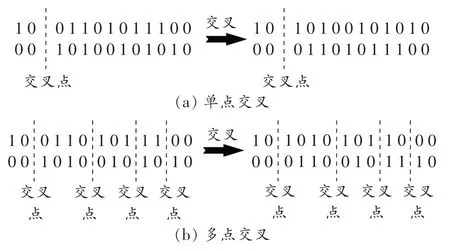
图2 不同的相位旋转序列交叉方案

3 仿真校验

本节对IGA-SLM降低VLC DCO-OFDM系统PAPR的能力进行仿真和校验。仿真参数设置如下:DCO-OFDM系统子载波数为128,调制方式采用4QAM,相位旋转序列由[1,-1]组成,序列的个数为16；IGA-SLM迭代次数为100,自适应系数β=1.10,差异系数γ=0.10,立即淘汰率α=1.20,交叉概率Pc=0.80,调整区间[0.60,0.95],变异概率Pm=0.19,调整区间[0.05,0.30],交叉点数调整区间[2,6]。采用互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)来直观地观察系统的PAPR性能。

图3所示为VLC DCO-OFDM系统在不同算法下的CCDF曲线。图中反映了系统在使用不同算法的情况下,其PAPR值超过PAPR0的概率大小,如系统使用IGA-SLM算法时,系统的PAPR值超过6.78 dB的概率为10-3。仿真结果表明,IGASLM可显著降低VLC DCO-OFDM系统的PAPR；此外,由于GA-SLM存在过早收敛现象,其PAPR性能与SLM算法几乎相同。

图4所示为IGA-SLM在迭代过程中最佳PAPR值与平均PAPR值的关系曲线。由图可知,随着迭代的不断进行,IGA-SLM逐步搜索出PAPR性能更好的相位旋转序列；但与此同时,算法的复杂度也在增加。因此,在实际应用时需要根据实际需求对系统性能和迭代次数进行平衡选择。

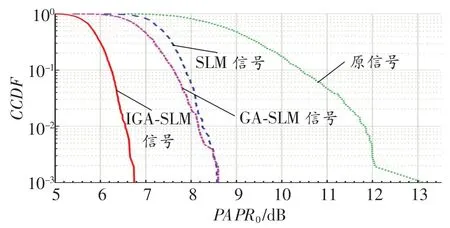
图3 不同算法下的CCDF对比分析

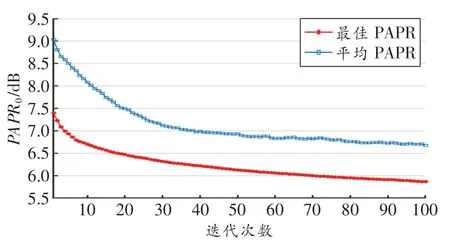
图4 最佳PAPR与平均PAPR的关系曲线

在VLC DCO-OFDM系统中,系统的子载波数是一个非常重要的参数。图5所示为IGA-SLM在不同子载波数下的CCDF曲线。由图可知,在IGASLM下,VLC DCO-OFDM系统的子载波数量越少,系统的PAPR性能越好。

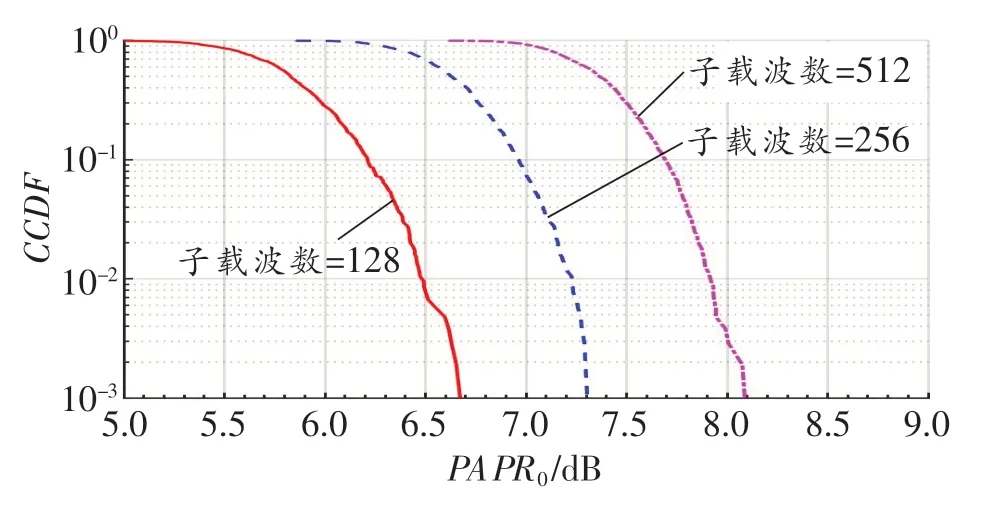
图5 不同子载波数下的CCDF

4 结束语

本文针对VLC DCO-OFDM系统中存在的高PAPR问题进行了优化研究,在分析了SLM算法的缺陷和改进型遗传算法的优势之后,提出了IGASLM。仿真结果表明,IGA-SLM可以显著降低VLC DCO-OFDM系统的PAPR,并且随着系统子载波数的减少和算法迭代次数的增加,系统的PAPR可以更进一步地降低。