基于色散渐减光纤环镜中脉冲对传输特性研究

史圣达,张巧芬

(广东工业大学a.机电工程学院; b.精密微电子制造技术重点实验室,广州 510006)

0 引 言

现代通信中产生和传输高功率、严格线性啁啾的高质量超短脉冲是光脉冲传输领域的重点[1-3]。光脉冲在传输过程中会因为色散和非线性效应而发生展宽[4-6]。目前解决脉冲展宽问题的方法有很多,例如:自相似脉冲、孤子的非绝热压缩和光纤光栅压缩等等[7]。常用的脉冲压缩方法是使用孤子的非绝热压缩对单个脉冲进行压缩,虽然会得到较高压缩比的脉冲,但是压缩后的脉冲会产生较大的基座,影响脉冲的压缩质量[8-10]。近年来使用孤子非绝热压缩和光纤环镜的光开关特性对超短脉冲进行压缩可以得到高压缩比、无基座和高质量的超短脉冲[10]。Ablowitz M J早在1981年就提出了孤子是非线性薛定谔方程的稳态解,从而奠定了孤子的理论研究[11]；刘晶会等人分析了光脉冲在色散渐减光纤中的传输特性[12]；杨亚培应用部分相干光的理论,得出了光纤环镜中光脉冲的相干性[13]。但大多数讨论的都是单个脉冲在光纤环镜中的压缩特性,对于脉冲对的压缩特性的研究少之又少。本文研究的目的在于分析脉冲对在色散渐减光纤环镜中的传输特性。利用色散渐减光纤环对脉冲对进行压缩,以便得到高质量的压缩脉冲对。

1 脉冲对传输的理论分析

色散渐减光纤环镜是由3 dB耦合器和两段色散渐减光纤构成的,如图1所示。两段色散渐减光纤分别是AB段五阶超高斯型色散渐减光纤和BC段高斯型色散渐减光纤。

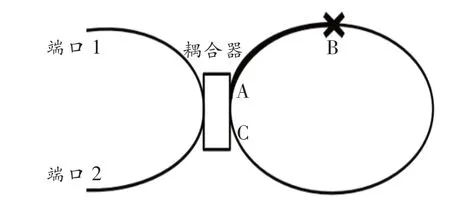
图1 光纤环镜结构图

脉冲在色散渐减光纤环镜中传输时满足非线性薛定谔方程,并在反常色散区传输时演化成光孤子[13]。

薛定谔方程表示为

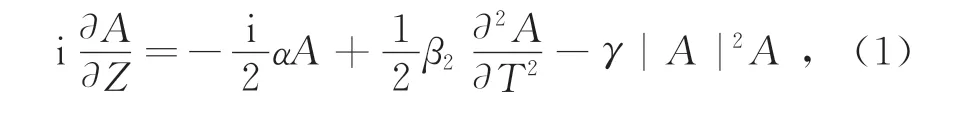
式中:i为虚数；A为脉冲包络的慢变振幅；T为随脉冲以群速度移动的时间；Z为传输距离；β2为光纤二阶色散系数；α为损耗系数；γ为非线性系数。脉冲由端口1输入,从端口2输出。本文输入脉冲采用的是双曲正割脉冲,因为双曲正割脉冲与光孤子有固有的联系且在传输过程中会演化成抛物线型。输入的双曲正割脉冲对表示为

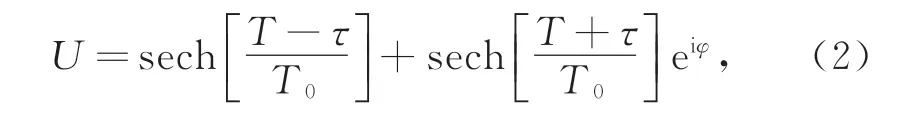
式中:sech为双曲正割函数；τ为脉冲的时延；φ为脉冲的相位；T0为初始脉宽。色散渐减光纤是由两部分组成的,AB段长度为L1,BC长度为L2,其二阶色散系数分别为

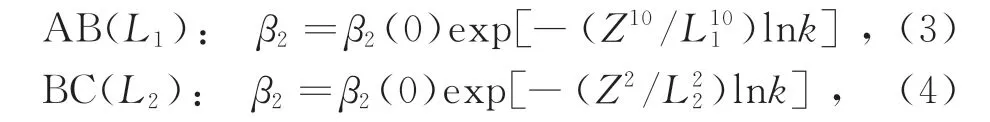
式中,k为光纤起始端与末端二阶色散系数的比值。在传输过程中利用孤子的非绝热压缩效应可以对脉冲对进行较大的压缩,但压缩后会产生较大的基座,影响压缩脉冲的质量。可利用光纤环镜的光开关特性来消除基座。光纤环镜的光开关特性是指两个相向传输的光脉冲,在一定的光纤长度下会发生干涉,使初始脉冲中心处的相移相差π,而两翼的相移差小于π。当两脉冲再次经过耦合器时,脉冲中心处的相移差变为2π,两脉冲干涉相长,而两翼处的相移差近似于π,干涉相消,故可得到较高质量的压缩脉冲。

2 模拟仿真与数值分析

本文设色散系数比值k=30,初始群速度色散β2(0)=-20 ps2/km,非线性系数γ=3 W-1km-1,输入的初始功率p0=0.3 W,光纤损耗为α=0.01 dB/km。为了研究色散渐减光纤环镜对脉冲对的压缩效果,首先要了解色散渐减光纤环镜中每段色散渐减光纤的色散变化情况。图2所示为五阶超高斯型色散渐减光纤和高斯型色散渐减光纤的色散变化曲线。

图中虚线为五阶超高斯型色散渐减光纤的色散变化函数,可以看到随着光纤长度的增加,色散曲线先是缓慢变化,当光纤长度为1 km时,色散曲线逐渐变陡峭,当光纤长度为5 km时曲线再次趋于平缓。图中实线为高斯型色散渐减光纤的色散变化函数,可以看到随着色散渐减光纤环镜长度的增加,色散曲线较陡峭,当光纤长度为5 km时,色散曲线趋于平缓。本文研究脉冲对在色散渐减光纤环镜中的传输特性,根据时延τ和相位φ的变化来分析脉冲对由非重叠区到重叠区的传输特性。当φ=π时,根据时延的变化观察脉冲对的传输和压缩特性变化。当时延τ=20、10、5和2 ps时,脉冲时域变化和提取的部分时域特征如图3所示。

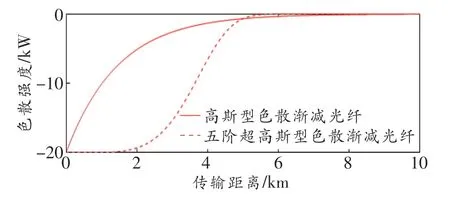
图2 色散变化曲线

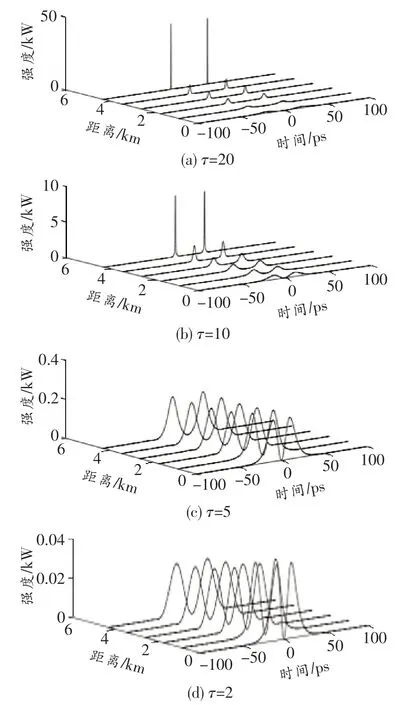
图3 φ=π,τ=20、10、5和2时的脉冲时域变化

由图可知,当τ=10和20时,脉冲对之间的时延足够大,使得脉冲对传输时处于非重叠区互不干扰。当τ=2和5时,脉冲没有被压缩反而逐渐展宽,这是由于脉冲时延较短,使得脉冲对之间部分区域重叠,重叠区域发生相长和相消干涉,从而影响了脉冲的压缩。图4所示为φ=π时脉冲时域传输曲线中的初始脉冲和压缩脉冲,虚线为初始脉冲,实线为压缩脉冲。由图可知,当τ=10和20时,脉冲具有极高的压缩比,且没有基座的产生。当τ=2和5时,脉冲没有明显的压缩,甚至因为光纤损耗和脉冲干涉使得脉冲功率减弱,此时的脉冲因为时延太短而相互作用,产生了局部相移和重叠,影响了脉冲压缩效率。为了进一步得出脉冲在传输过程中的压缩特性,下面来分析传输过程中啁啾的变化。图5所示为τ=20、10、5和2时的啁啾变化。

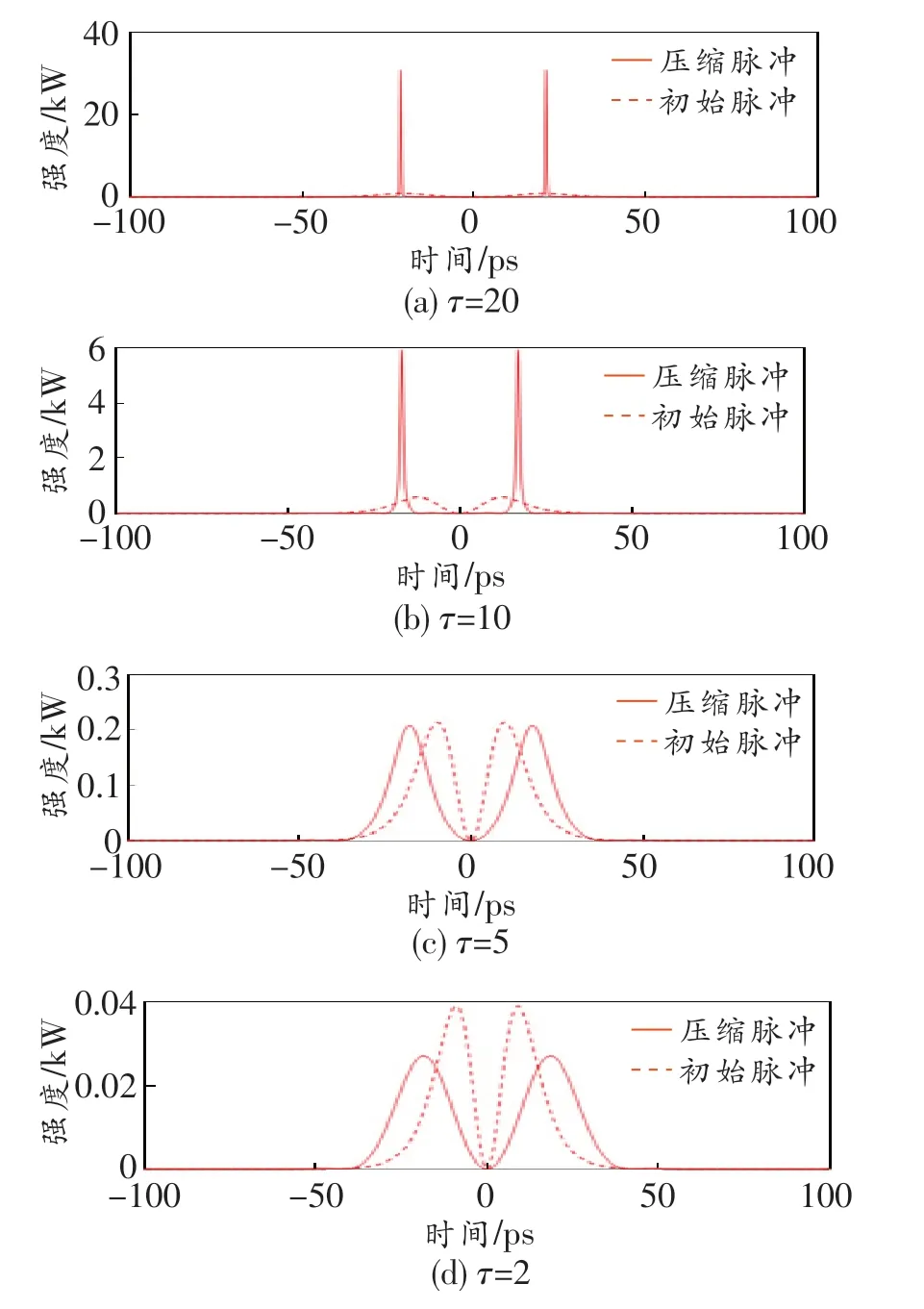
图4 φ=π时脉冲时域传输曲线中的初始脉冲和压缩脉冲

由图可知,当τ=20、10、5和2时,脉冲具有局部的线性啁啾,随着时延的增大,啁啾的线性范围增加,脉冲压缩比变高。说明啁啾的线性范围越大,脉冲的压缩特性就越好。当τ=10和20时,两个脉冲有自己的局部线性啁啾；当τ=2和5时两个脉冲的啁啾混合在了一起近似为一个啁啾。这是因为脉冲对之间发生了交叉相位调制效应而引起脉冲对之间发生干涉,导致啁啾产生了剧烈的振荡结构。脉冲啁啾的分布与自相位调制和群速度色散有关。在反常色散区群速度色散所产生的啁啾为负啁啾,自相位调制所产生的啁啾为正啁啾,开始传输时群速度色散占主导地位,总啁啾逐渐减小,随着传输距离的增加,色散渐减光纤的二阶色散系数是逐渐减小的,故当群速度色散和自相位调制效应平衡时,此时的啁啾最小,脉冲的压缩效果最佳。图中时延较小时,脉冲之间的距离小于脉宽,从而使得部分脉冲发生重叠现象,影响脉冲的压缩。当时延差足够大时,重叠部分会较小,脉冲间的相互作用对脉冲的压缩效果几乎没有影响。

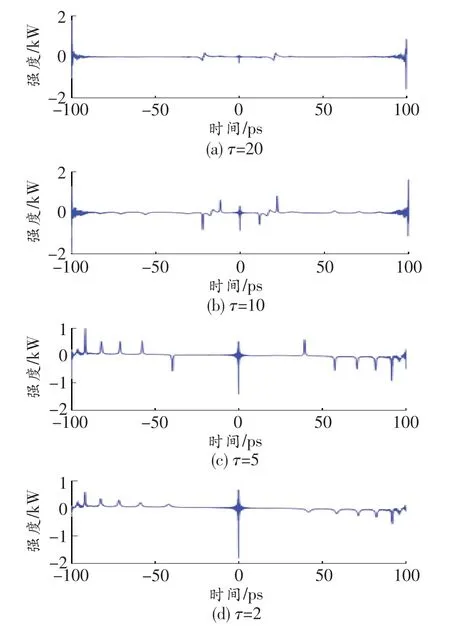
图5 τ=20、10、5和2时的频率啁啾

为了探讨脉冲对在色散渐减光纤环镜中的传输特性与单模光纤中传输特性的不同,我们对比了当脉冲相位φ=π、τ=20时的脉冲对时域变化曲线,如图6所示。由图可知,脉冲对在单模光纤中传输时由于光纤损耗和孤子特性的原因,脉冲对强度随着传输距离的增加而下降,且脉冲对在传输过程中没有被压缩反而被展宽,与在色散渐减光纤环镜中相比,脉冲对的传输质量明显下降,无法形成高功率超短压缩脉冲,应用的意义不大。

当φ=π/2时,根据时延的变化观察脉冲对的传输特性变化和压缩特性变化。图7所示为φ=π/2、τ=20、10、5和2时的频率啁啾。图8所示为φ=π/2、τ=20、10、5和2时的脉冲时域变化。由图可知,不同时延下的脉冲对具有不同的能量,这是因为脉冲的相位相差为π/2,在开始传输时时延较小会使得两个脉冲的重叠区域较大,第2个脉冲的部分能量会叠加在第1个脉冲上,时延越短重叠部分越大,导致两个脉冲会出现能量差。随着传输距离的增加,脉冲被压缩,故会出现两个明显的峰值。开始传输时随着脉冲时延的减小,两个脉冲之间的距离变短,脉冲之间会发生近似于完全重叠的现象。随着传输距离的增加,只有脉冲压缩到一定程度时两个脉冲才会分开,两个脉冲重叠时间越长,第2个脉冲所剩余的能量就越低。

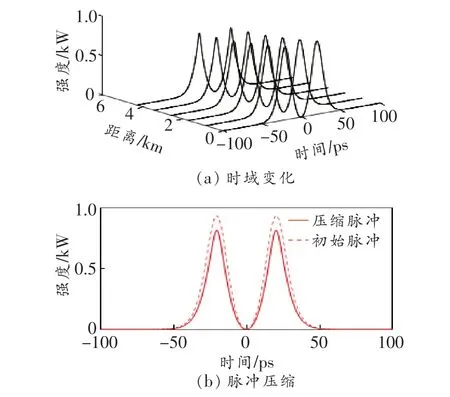
图6 φ=π,τ=20时脉冲在单模光纤中的时域变化

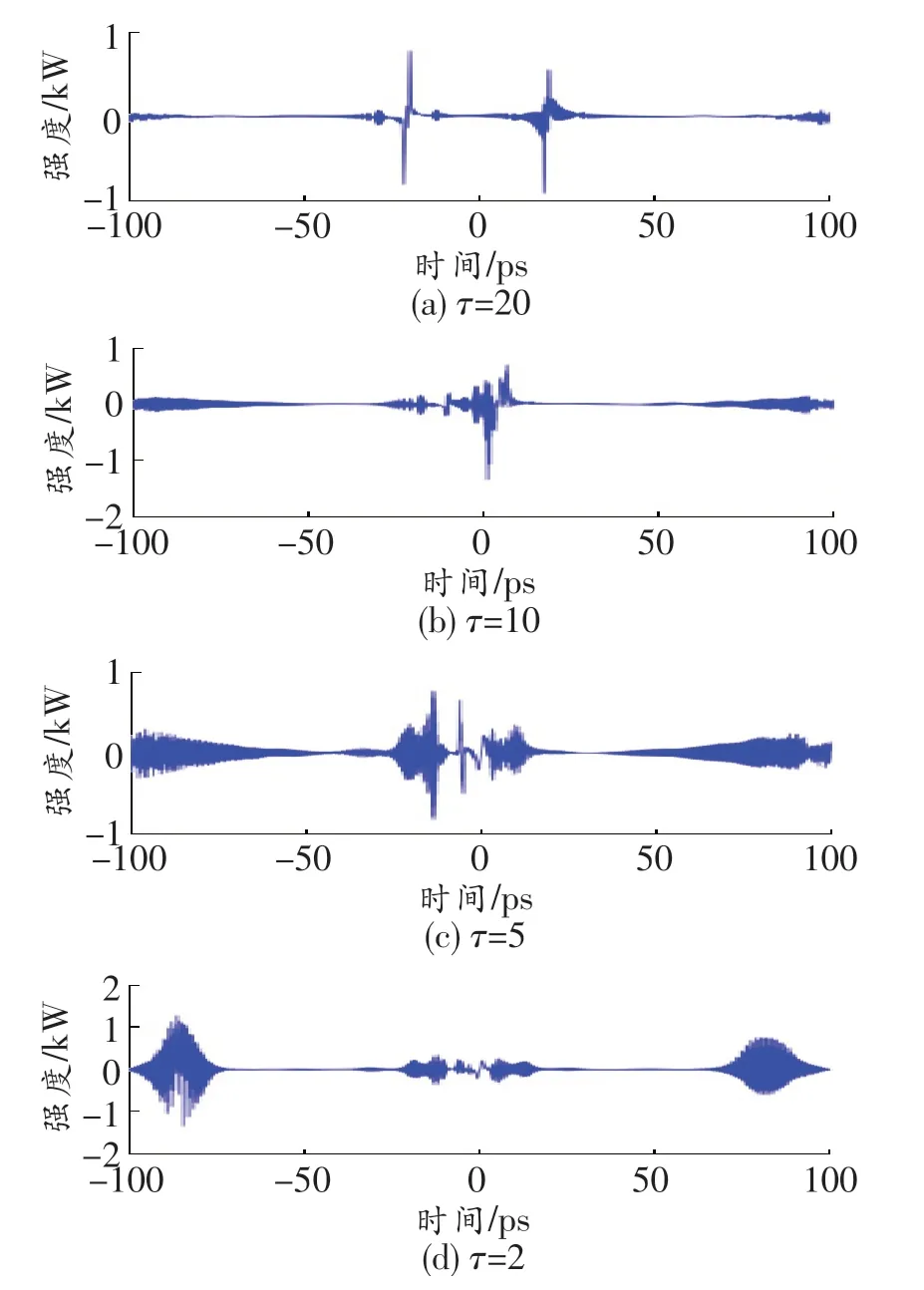
图7 φ=π/2,τ=20、10、5和2时的频率啁啾

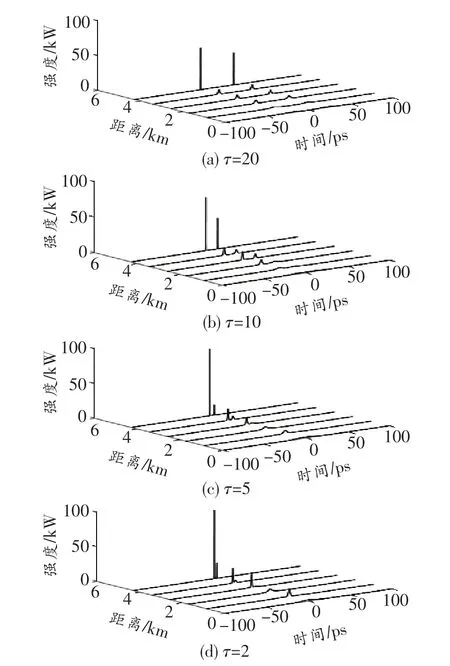
图8 φ=π/2,τ=20、10、5和2时的脉冲时域变化

随着啁啾的变化脉冲对的压缩情况 如图9所示。由图可知,当τ=20、10、5和2时脉冲都具有局部的线性啁啾。当τ=10和20时,两个脉冲的啁啾有明显的分解线,两个脉冲的啁啾开始时维持自己的形状,传输一段时间后两个脉冲啁啾相互作用。但是当τ=2和5时,两个脉冲的啁啾集合混合在了一起近似于一个啁啾,这是因为两个脉冲之间的相位较小,导致脉冲之间发生相互作用,使得啁啾两端的振荡结构加剧,中间部分重合。

当φ=π/2时,分析脉冲对在色散渐减光纤环镜中的传输特性与单模光纤中传输特性的不同,我们对比了τ=20时的脉冲对时域变化曲线,如图10所示。由图可知,因为两脉冲初始相位的原因,脉冲之间在传输开始即相互作用,但由于在单模光纤中传输,自相位调制和群速度色散对脉冲对的传输特性影响较大,脉冲对随着传输距离的增加而逐渐展宽,脉冲之间的信号重叠无法准确地传输信息。而脉冲对在色散渐减光纤环镜中传输时,因为色散渐减光纤环镜对脉冲有压缩作用,故在传输一段距离后脉冲对分开独自压缩,可获得高功率超短脉冲。

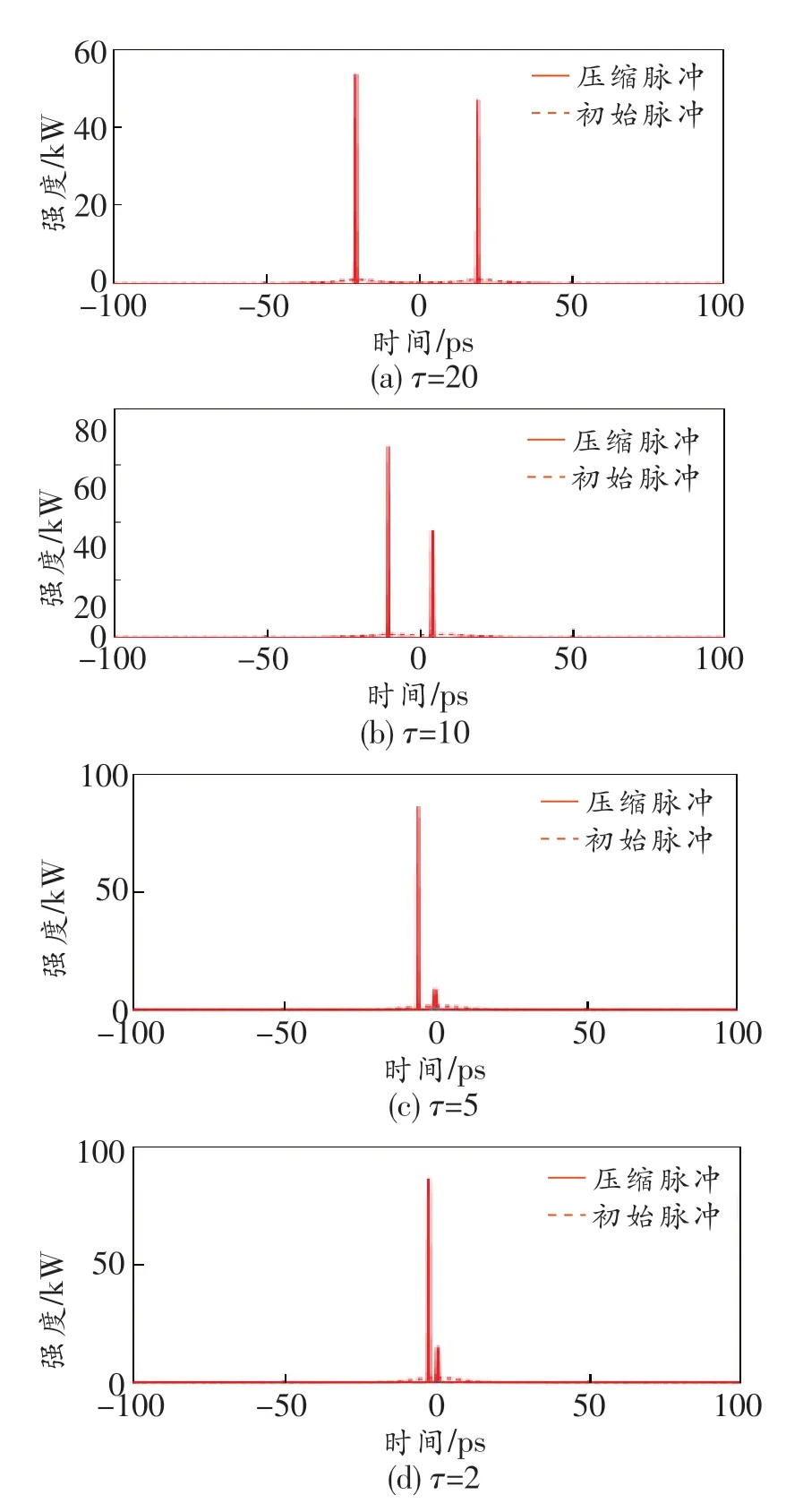
图9 φ=π/2时,脉冲时域传输曲线中的初始脉冲和压缩脉冲

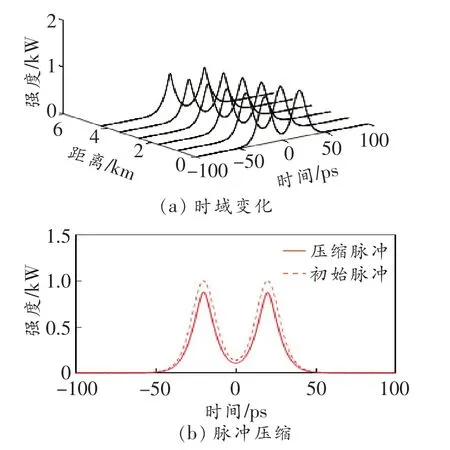
图10 φ=π/2,τ=20时的脉冲在单模光纤中的时域变化

3 结束语

本文研究分析了脉冲对在色散渐减光纤环镜中的传输和压缩特性,经过模拟实验得出以下结论:

(1)当φ=π,τ=10和20时,脉冲对之间的时延足够大,使得脉冲传输时在非重叠区互不干扰,具有单个脉冲的传输特性。当τ=2和5时,脉冲在光纤环镜中传输时没有被压缩反而逐渐展宽,这是由于脉冲时延较短,使得脉冲对之间部分重叠,重叠区域形成干涉,从而影响了脉冲的传输和压缩特性。

(2)当φ=π/2,τ=2、5、10和20时,脉冲对之间的相位差较小,在传输时脉冲对之间会有一部分重叠区域,第2个脉冲的部分能量会叠加在第1个脉冲上,时延越短重叠部分越大,两个脉冲重叠时间越长,导致第2个脉冲所剩余的能量就越低,致使两个脉冲会出现能量差。

(3)当τ=2、5、10和20时,脉冲具有局部的线性啁啾,随着时延的增加,啁啾的线性范围增大,压缩效果更好,说明啁啾的线性范围越大,脉冲的压缩特性就越好。当τ=10和20时,两个脉冲的啁啾有明显的区分,并且啁啾的线性部分较多；当τ=2和5时,两个脉冲的啁啾混合在一起近似一个啁啾,且脉冲对之间的相互作用使得啁啾两端产生了剧烈的振荡结构。脉冲之间的干涉也使得啁啾的线性部分变少。

总之,我们分析了脉冲对在色散渐减光纤环镜中的传输特性,在传输过程中它们首先在重合区域正弦拟合振荡,然后因为光纤环形镜的压缩特性,两脉冲逐渐分开,随后脉冲独立演化。此外,在压缩后我们得到了一对压缩比极高的高质量超短脉冲。