Kumaraswamy分布下负载共享并联系统的参数估计

李丹青， 熊文洁， 张正成

(1.兰州交通大学 数理学院，甘肃 兰州 730070；2.海南师范大学 数学与统计学院，海南 海口 571158)

在可靠性理论中，Rosen[1]率先使用负载共享系统模型来研究复合材料的可靠性，介绍了一种复合材料失效的理论和实验方法，一束纤维可视为受恒定负载影响的并联系统，当受到平行于纤维方向的单轴拉伸负载时，纤维被视为一个统计分布，在施加的应力下导致纤维失效。之后，关于可靠性系统的研究便渗入了各行各业，统计学家们纷纷开始研究可靠性系统并将其运用到实际中。Boland 等人[2]讨论了在系统中如何分配冗余组件的位置从而优化系统寿命的问题，他们考虑了主动冗余和备用冗余，特别是在串联和并联系统中获得了广泛的结果。在大多数关于负载共享系统的研究中，系统的性能仅针对元件的寿命遵循指数分布的情况进行了研究，Yun 和Cha[3]研究了当系统中元件的寿命是任何连续的随机变量时，考虑负载共享并联系统的可靠性及其负载分配问题。关于负载共享系统的可靠性更详细的问题可见文献[4-9]。

Kumaraswamy分布[10]是在1980 年由Kumaraswamy研究水力学当中的日常降雨量提出的，它是一种在(0，1) 范围内取值的双参数连续型分布，与Beta 分布有许多相同的特征但其分布函数有非常简单的显式，这个特征对这个分布的模拟计算与应用带来很大的方便。Nadarajah[11]给出了Kumaraswamy分布的几种一般形式及其相关应用。MITNIK[12-13]在过去研究的基础上扩展了Kumaraswamy分布的属性特征，并提出了两种简单的Kumaraswamy分布变量属性：线性转化和取幂形式下该分布具有紧凑型特征.该分布作为寿命模型在可靠性方面非常有用，但关于负载共享并联系统的研究却被忽略了。

Kumaraswamy分布的可靠性函数：

(1)

Kumaraswamy分布的密度函数：

f(x)=αβxα-1(1-xα)β-1,00,β>0

(2)

在早期，KIM 和KVAM[14]考虑了k个元件并联的负载共享系统，元件的故障率取决于系统中剩余存活的元件个数.起初，各元件独立同分布且具有共同的失效率θ，直到第一个元件失效后，剩余存活元件的失效率为γ1θ，第二个元件失效后，剩余存活元件的失效率为γ2θ(γi>0,i=1,2,…,k-1)等等。在基于负载共享规则是未知的前提下，根据最大似然估计导出负载共享系统参数γi,θ的统计推断方法。KVAM 和PENA[15]基于独立同分布的k个元件并联的负载共享系统，导出了等负载分配模型中负载分配参数的估计值。在等负荷分配模型中，在第一个元件失效后，其余元件的故障率从r(t)变为γ1r(t)，然后在下一次故障后变为γ2r(t)等等.然后，他们获得了元件基线累积危险函数的半参数估计，并讨论了它的渐近分布。SINGH 等[16]通过在开始时使用恒定负载，然后在一定数量的元件故障后线性增加失效率，进一步修改了KIM 和KVAM[14]的模型。PARK[17]研究了当元件的寿命分布是指数或Weibull 分布时这类系统的参数，并且在元件为指数分布的情况下，采用KIM 和KVAM[14]中的模拟数据，在相等负载共享的规则下获得了闭合形式的MLE 和渐近最佳无偏估计(ABUE) .HUANG[18]研究了EKD 家族(Exponentiated Kumaraswamy-Dagum) 分布函数性质，包括密度函数、风险函数、可靠性等，并引入实例比较EKD 与其他函数的差异.最近，ZHANG 和Balakrishnan[19]研究了一种通用的负载共享并联系统，其中系统元件的寿命是任意连续的随机变量，然后考虑具有两个独立元件的串联系统中一个负载备用的最佳分配问题，并讨论了某些特定系统的参数的最大似然估计。

1 建立模型

1.1 模型的描述

首先我们建立一个负载共享并联系统的模型来估计出它的参数，假设这个模型具有以下特征:

⑴n个独立同分布的负载共享系统中各包含k个元件，它们带有一个共同的恒定负载,该负载在其工作元件中均匀分配;

⑵对这n个系统进行测试并记录其故障时间，设Tij(i=1,2,…,n;j=1,2,…,k)是第i个并联系统中第(j-1)和第j个元件失效之间的时间间隔;

⑶系统内一个元件的失效会增加剩余存活元件的负载;

⑷起初，元件的寿命服从参数为α1,β1的Kumaraswamy分布，在元件第一次失效后，初始参数由α1,β1变为α2,β2，第二次失效后，参数由α2,β2变为α3,β3，直到元件第(k-1)次失效后，最后一个元件的参数变为αk,βk;

⑸负载共享参数α1,α2,…,αk和β1,β2,…,βk是独立且未知的。

1.2 系统密度函数的建立

从上述系统模型的特征中可以看出，起初，在具有k个元件的系统中，其失效率为h(t,α1,β1);当元件第一次失效后，系统剩余存活的(k-1)个元件的失效率为h(t,α2,β2);在第二次失效后，系统剩余存活的(k-2)个元件的失效率为h(t,α3,β3);最后，当第(k-1)个元件失效后，最后存活的那个元件的失效率为h(t,αk,βk)。

其中，服从Kumaraswamy分布的单个元件的失效率函数为：

h(t,α,β)=αβxα-1(1-xα)-1,00,β>0

(3)

那么，在(j-1)个元件完全失效后第j个元件的条件失效率函数为：

hTj|T(j-1)(t)=(k-j+1)h(t,αj,βj),j=1,2,…,k

(4)

根据以上假设(1)-(5) 及公式(4) 可以得出，随机变量Tij服从具有失效率(k-j+1)×h(t,αj,βj)的Kumaraswamy分布。所以，在第i个系统中第j个元件失效时间的密度函数为：

f(tij)=(k-j+1)αjβjtijαj-1·(1-tijαj)(k-j+1)βj-1，00,β>0

(5)

2 参数估计

设A=(α1,α2,…,αk)′，B=(β1,β2,…,βk)′存在于空间(0,∞)k中，其中αj>0，βj>0(j=1,2,…,k)，则第i个负载共享并联系统模型的似然函数为：

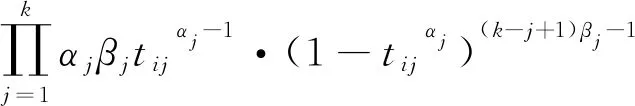
基于n个独立同分布系统的似然函数为：

这里，T={tij,i=1,2,…,n;j=1,2,…,k}。所以，相应的对数似然函数为：

然后便可以根据这相应的2k个对数似然方程：

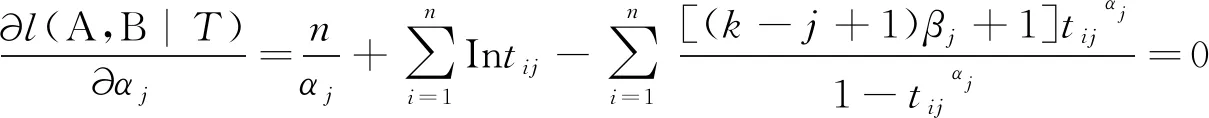
(6)

(7)

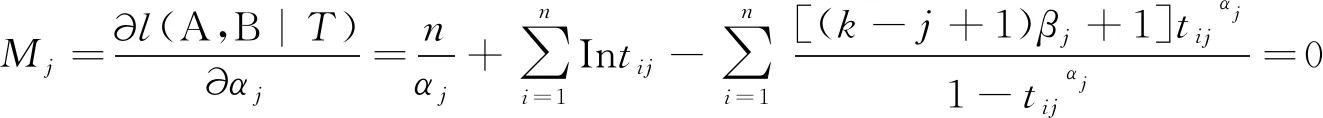
(8)

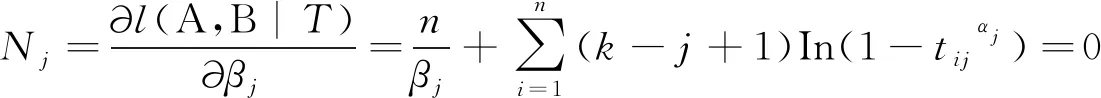
(9)

像高斯-赛德尔迭代法就能很好地求解出这2k个参数的值,一般分为以下几步：

⑴选择合适的初始值α1(0),…,αk(0)，将其代入Nj=0中求出βk的解，将其表示为βk(1)；

⑵将βk(1)代入Mj=0中求出αk的解，将其表示为αk-1(1)；

⑶同样将α1(0),…,αk-1(0),αk(1)代入Nj=0中求出βk-1的解，将其表示为βk-1(1)；

⑷将βk-1(1)代入Mj=0中求出αk的解，将其表示为αk-1(1)；

⑸依次类推，在最后的表达式中固定其他变量来求解αj和βj，得出αj(1),βk-1(1)使得Mj=0,Nj=0；

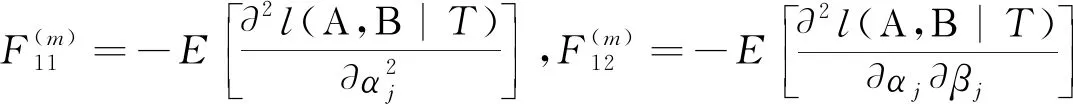
接下来，为简单起见，我们来研究α=1时Kumaraswamy分布的最大似然估计值(MLE) 。此时，具有一个参数β的可靠性函数是：

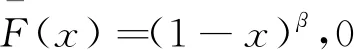
相应的概率密度函数为：

f(x)=β(1-x)β-1,0x1,β>0

并且第i个系统的第j个失效时间的概率密度函数为：

f(tij|αj)=(k-j+1)βj(1-tij)(k-j+1)βj-1，i=1,2,…,n;j=1,2,…,k。

(10)

所以，第i个系统(i=1,2,…,n)的似然函数是：

且基于n 个样本的似然函数是：

(11)

则其对数似然函数为：

通过对上式进行微分，我们可以得出一个对数似然方程：

因此，我们便可以得出其最大似然估计值(MLE) 为：

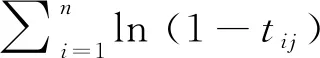
根据相对速率(RE) ，我们可以得出ABUE 优于MLE ，即使在n→∞时它的极限趋于1 ，但是这细微的差异对于小样本来说也是不可忽视的。此外，

显然，k×kHessian 矩阵{∂2l/∂βi∂βj}是负定的，所以在这个子空间中存在一个向量B使 得产生(11) 的全局最大值。

在空间(0,∞)k中让Β=(β1,β2,…,βk)′，这里，βj>0(j=1,2,…,k)。那么，参数向量Β的Fisher 信息矩阵为

为参数构建基于似然比的联合置信度，观察到的Fisher 信息矩阵F的倒数提供了大样本正态分布中的协方差的估计。对于大样本，Β∈(0,∞)k的近似1-α置信椭球为

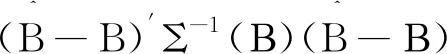
3 模拟研究

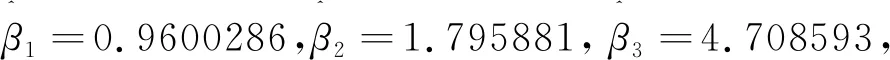
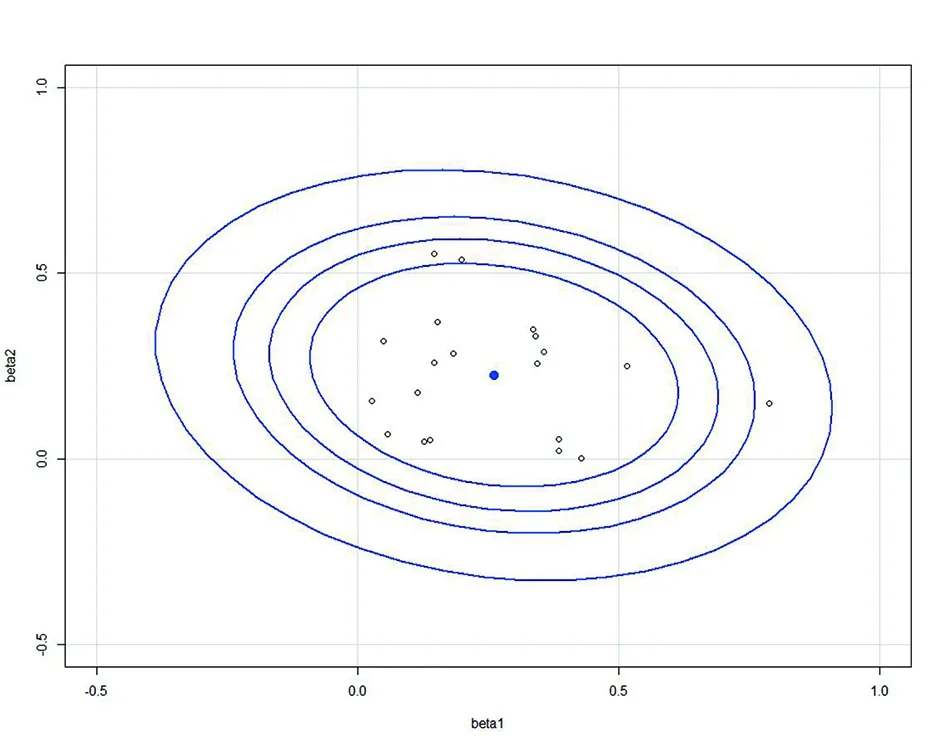
图1 (β1,β2)的(80%，90%，95%，99%) 的置信椭圆图

表1 失效时间数据

表2 MLE 和ABUE

表3 MLE和ABUE的经验偏差(bias)及均方误差(MSE)

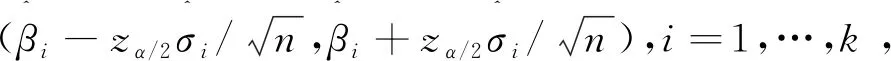
在下文中，分别构造了基于Bootstrap 技术的两种参数置信区间，如百分位bootstrap(boot-p) 和bootstrap-t(Boot-t) 方法，更多细节详见Efron[21]和Hall[22]。

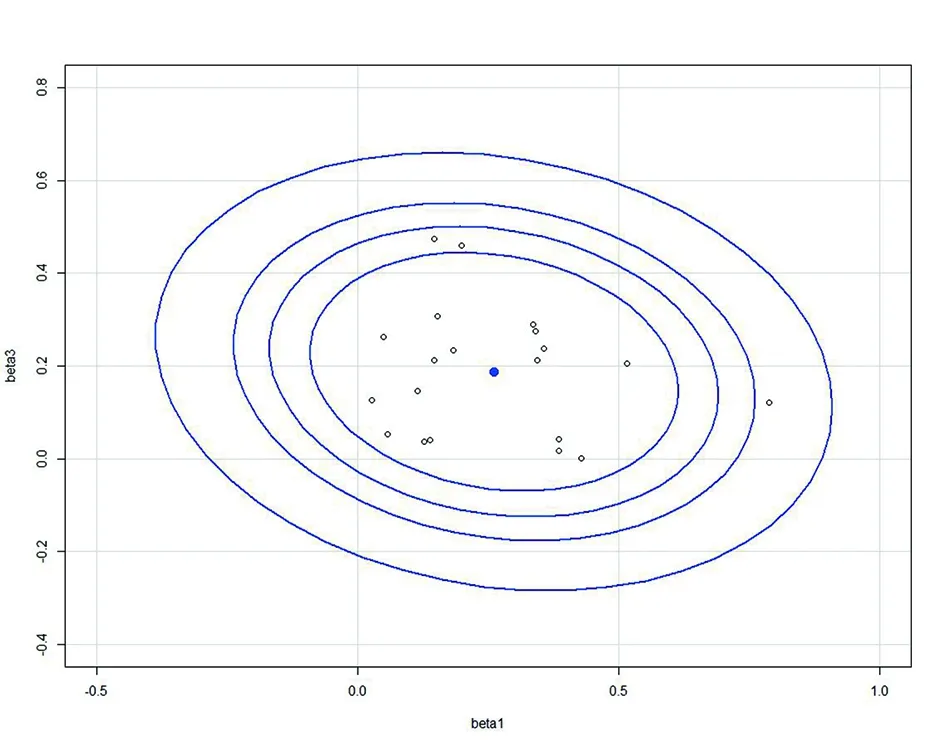
图2 (β1,β3)的(80%，90%，95%，99%) 的置信椭圆图

3.1 Boot-p算法

⑴用公式(10) 生成n个样本Tij(i=1,2,…,n;j=1,2,…,k)；

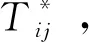
⑶重复步骤2B次；

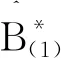
3.2 Boot-t 算法

⑴用公式(10) 生成n个样本Tij(i=1,2,…,n;j=1,2,…,k)；

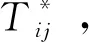
⑷重复步骤2-3B次；

在表4中，我们仍旧设置k=3,β1=1,β2=2,β3=5。并且在R 语言软件的帮助下，我们可以在样本数n分别为20，50，75，100的情况下计算不同的估计值，标准误差(SE) 及 其95% Bootstrap 置信区间(CI) 的宽度.这里我们采用了5000次Bootstrap程序(B=5000)。从表4可以看出，当样本数逐渐增多时，参数估计的标准误差越小，区间宽度越小，故参数的点估计和区间估计更精确，且由于Boot-t 是由Boot-p 方法进行改进得到的，因而比Boot-p 方法更加准确.结合表2 和表4 我们可以看出，当样本量同为20 时，Bootstrap 估计值均优于MLE 和ABUE ，由此可见，Bootstrap 技术的优越性。

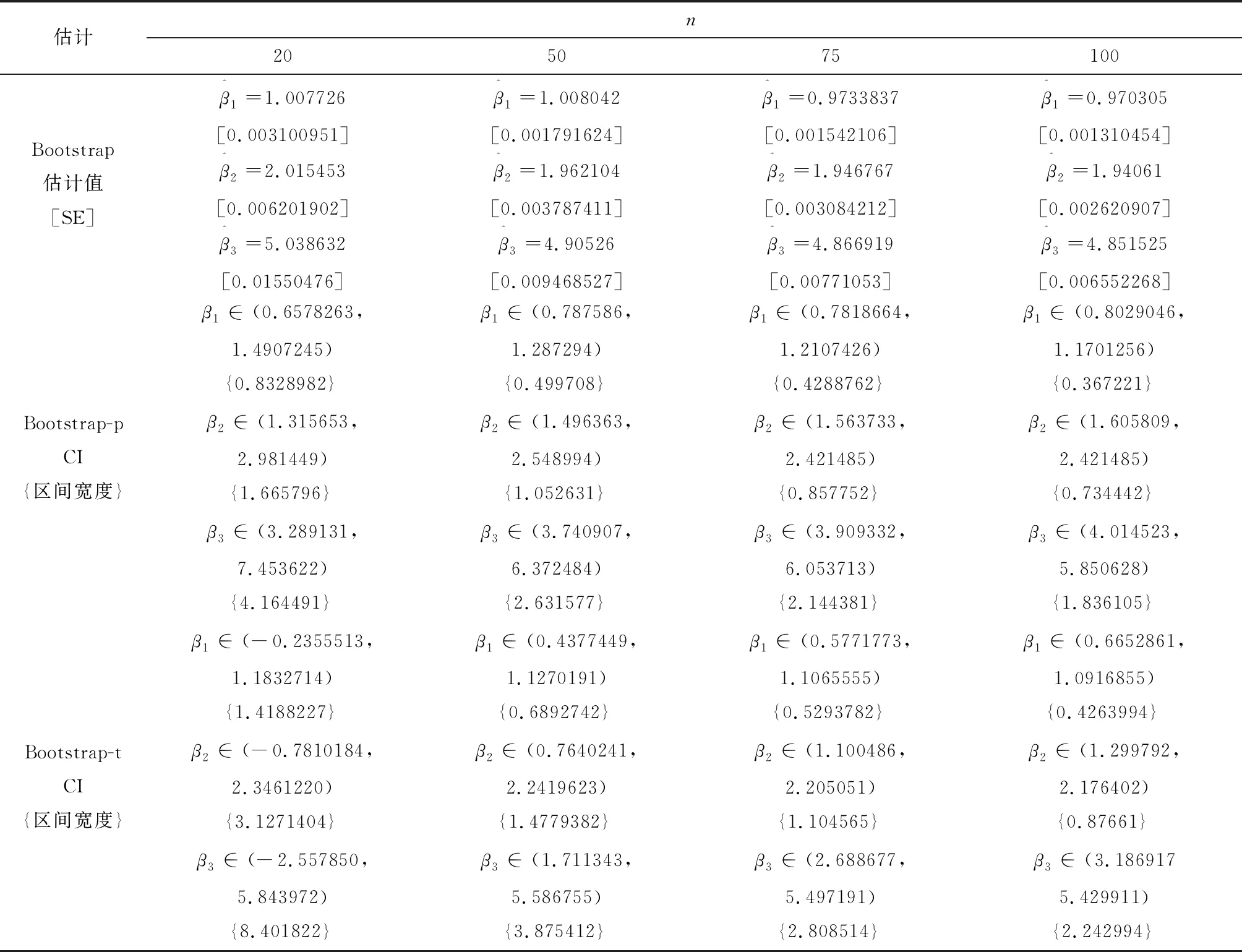
表4 95% bootstrap 置信区间(CI)

4 总结

在本文中，我们研究了负载共享系统可靠性的参数估计方法.在寿命遵循一般的负载 共享原则的基础上，我们考虑了元件的基础分布为kumaraswmy分布。

我们给出了适当的迭代方法来讨论具有两个未知参数的分布的参数估计器。此外，构建了估计统计量的渐近分布。对于简化的模型，我们通过模拟的数据提供了闭合形式的MLE，ABUE 和参数的置信区间。