半空间上方金属腔时域屏蔽效能的计算及分析

曹乐 周远国 付周兴

摘 要：針对复杂半空间格林函数难以计算的问题，提出一种改进的半空间时域有限差分（FDTD）方法，实现有耗半空间上方细缝金属腔的时域屏蔽效能的高效计算和分析。首先，采用广义传播矩阵法计算半空间复反射系数，再结合傅里叶变换得到半空间时域反射回波。其次，将直接入射波和半空间反射波共同引入到FDTD计算区域，半空间的影响通过反射波体现，从而回避计算形式复杂的半空间格林函数，实现金属腔内部观察点的耦合场及时域屏蔽效能的快速计算。与传统半空间FDTD方法相比，计算方法的误差在0.5%以内，而计算效率提升52%，证明了计算方法的正确性及有效性。结果表明，由于半空间的反射效应，细缝腔体内部观察点的场强增大，时域屏蔽效能显著下降。计算方法可用于半空间背景下腔体时域屏蔽效能的快速分析，从而为电子系统电磁耦合效应的评估提供参考。关键词：时域屏蔽效能;有耗半空间;半空间FDTD;屏蔽腔;电磁脉冲中图分类号：TM 154

文献标志码：A

文章编号：1672-9315（2020）06-01096-06

DOI：10.13800/j.cnki.xakjdxxb.2020.0621开放科学（资源服务）标识码（OSID）：

Evaluation of time-domain shielding effectiveness for

metallic cavities above lossy half-space

CAO Le1，2，ZHOU Yuan-guo2，FU Zhou-xing1

（1.

College of Electrical and Control Engineering，Xian University of Science and Technology，Xian 710054，China;

2.School of Electrical Engineering，Xian Jiaotong University，Xian 710049，China;

3.College of Communication and Information Engineering，Xian University of Science and Technology，Xian 710054，China）

Abstract：In order to solve the problem that the half-space Green function of complex media is difficult to calculate，an improved half-space FDTD algorithm that avoids the half-space Green function is proposed to achieve the efficient computation analysis of the time-domain shielding effectiveness（SE）of the metallic cavities above the lossy half-space.Firstly，the generalized transition matrix method and Fourier transform are used to calculate the reflected wave of half-space.Secondly，with the direct incident wave and the reflected wave  introduced into the calculation region，the coupling field of the observation point inside the cavity under different incident conditions is calculated and analyzed.Compared with the traditional half-space FDTD method，the calculation error here is within 0.5%，and the calculation efficiency is increased by 52%，which proves the correctness and effectiveness of this method.The numerical results show that due to the reflection effect in the half space，the field strength increases，and the time-domain shielding effectiveness decreases significantly.The method in this paper can be used to quickly analyze the shielding effectiveness of the cavity in the time domain in the half-space background，thus providing a reference for the evaluation of the electromagnetic coupling effects of electronic systems.

Key words：time-domain shielding effectiveness;lossy half-space;FDTD method;shielding enclosure;electromagnetic pulse

0 引 言

金属屏蔽腔是电磁兼容设计与防护中保护电子设备、器件不被电磁脉冲干扰的重要手段。然而，为了保障电子设备的正常工作，屏蔽腔往往需要开各种类型的孔缝，而这些孔缝将使得电磁脉冲能量得以进入到电子设备内部。通过这样的“后门”耦合方式进入到电子设备的能量分布在整个系统内部，在特定频率下易发生共振而引起强耦合。相比“前门”耦合，“后门”耦合对系统的影响更大且难以消除。因此，开展金属腔体屏蔽效能的研究具有十分重要的意义[1-5]。以往屏蔽效能研究多在频域展开，主要包括MoM方法[6-8]，FDTD方法[9-12]，FEM方法[13-14]，及传输线方程方法等[15-16]，然而频域屏蔽效能并不能完全表征屏蔽体对时域脉冲场的屏蔽作用。基于此，时域屏蔽效能的概念被提出[17-19]。

同时，在实际应用中屏蔽腔往往放置在地面上方，因此屏蔽腔的电磁特征分析属于半空间及其上方目标的复合电磁问题。对于处于空气-地面2种介质分界面附近的腔体，其照射波不仅包含直接入射波，还包括半空间分界面的反射波[20-22]。鉴于此，在半空间背景下，电磁脉冲对屏蔽腔体内部产生的耦合效应必然与自由空间有所不同。文中采用改进的半空间FDTD方法计算了有耗介质上方含孔缝屏蔽腔体内部的3种典型的时域屏蔽效能，分析了不同条件下屏蔽效能的变化规律，最

后讨论了半空间及自由空间情形下屏蔽效能的变化。

针对半空间及其上方目标的复合电磁问题，目前存在2种求解思路。一种将半空间和目标等视为整体，进行整体的剖分建模，采用同一种数值方法求解;另一种对目标和半空间采用分别求解，再利用半空间格林函数计算两者的耦合。第1种方案计算需求会随目标高度升高急剧增大，计算效率不高;第2种方案需要引入半空间格林函数体现半空间的影响。然而，半空间格林函数形式复杂、计算繁琐，尤其是对多层平面介质和粗糙面介质，其半空间格林函数的推导和求解更加困难。

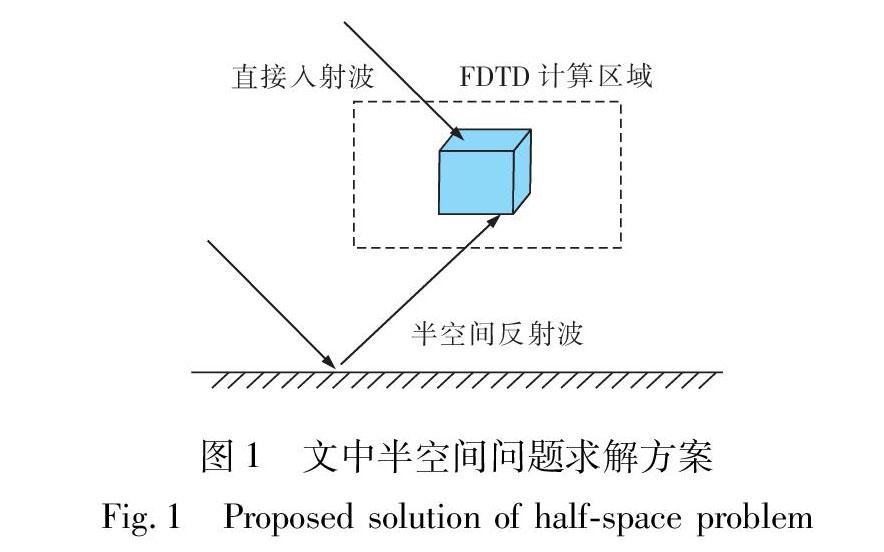
针对上述问题，文中提出一种解决半空间问题新思路。如图1所示，将总入射波分解为直接入射波及半空间反射波2部分，下半空间对目标电磁特性的影响通过反射波的引入而体现，避免使用形式复杂、难以计算的半空间格林函数，从而提高半空间问题的解决效率。

1 改进的半空间FDTD方法

1.1 半空间反射波的计算

本文采用传播矩阵方法计算半空间复反射系数，具体计算过程如下：首先，给出分层介质情形下的本征波;其次，定义状态方程并给出其解，最后，对分层介质的传播矩阵进行计算后就可以求解反射系数。

将入射电磁波分解为对z轴的TE波和TM波。根据传播矩阵方法，半空间情形下，反射系数表达式可写为[23]

RTE

=1-pTE01

1+pTE01

，

RTM

=1-pTM01

1+pTM01

（1）

式中 k1z，ε0，

ε1和μ0，μ1分别为真空及半空间介质的介电常数和磁导系数;

k0z

和k1z分别表示真空及半空间介质中波矢量k的z轴分量。

由反射系数可得到反射波水平极化分量和垂直极化分量为

Erh=|RTM|Efcosα0，Erv=|RTE|Efsinα0

（2）

式中 α0为入射波极化角，Ef为指定频率下入射电场的幅值。由以上公式计算出反射波的频谱再经过逆傅里叶变换，就得到了反射波的时域波形。

1.2 总入射波引入

在得到半空间反射回波后，文中基于等效原理，将直接入射波和半空间反射波共同引入到FDTD计算区域中。FDTD方法通常将计算区域分为总场区和散射场区，空间中的场为入射场和散射场之和。

Etot

=Einc+Escat

Htot

=Hinc+Hscat

（3）

式中 下角标tot，inc及scat分别表示总场、入射场、及散射场。如图2所示，FDTD方法一般根据等效原理，通过总场-散射场（total field-scatter field，TF-SF）边界直接在传播方向上投影并插值，从而将入射平面波源引入计算区域[24]。

半空间背景下目标的总入射波包含直接入射波及半空间反射波，相当于在自由空间中加入2个方向不同的入射源。在自由空间散射问题的FDTD计算中，可以预先设置一个一维FDTD迭代，然后利用等效原理将一维节点上的场值通过投影和插值的方法投影到FDTD的连接边界上获得入射平面波。在半空间情形下，多方向入射波引入时可以采用相同方法，可预先设置多个一维FDTD迭代，然后通过投影和插值获得多方向入射平面波，如图3所示。

这样通过2个一维FDTD迭代，就將直接入射波和界面反射波引入到了FDTD的总场边界，通过时域迭代计算，就可得到任意观察点的场值。

2 数值结果

2.1 算法验证及与传统半空间FDTD方法对比

算例1：为了验证文中方法中反射波计算方法的正确性，图4分别给出一维麦克斯韦方程方法[25]和文中方法计算有耗介质反射波的对比情况。一维麦克斯韦方程方法剖分网格δ=5×10-3m，时间步Δt=0.005×10-7 s.入射波为HEMP

E=kE0[exp（-αt′）-exp（-βt′）

]

（4）

式中 k=1.05，α=4.0×10-6 s，β=4.76×10-8 s

，由图4可见，文中方法与一维麦克斯韦方程方法结果吻合较好。

算例2：为了证明文中方法退化至自由空间情形下的正确性，分别采用商业软件CST Microwave Studio及文中方法计算了介质立方体

（

εr=4.0）内部观察点场值随时间的变化情况。入射波是脉冲宽度为1 ns的高斯脉冲。立方体边长0.32 m，FDTD剖分网格δ=8 mm，时间间隔Δt=0.006 25 ns，FDTD计算中CPML吸收边界节点为：-23∶23（

x方向）;-23∶23（y方向）;-23∶23（z方向），连

接边界为：-33∶33（x方向）;-33∶33（y方向）;-33∶33（z方向），观察点坐标为（0 m，0 m，0.2 m）。如图5所示，2种方法结果吻合较好，从而证明文中方法的正确性。

算例3：为了进一步证明文中方法的正确性及有效性，分别采用传统半空间FDTD方法和文中方法计算目标附近场强大小。目标为距离半空间分界面1 m，边长为0.64 m的介质立方体（

εr=4.0），下半空间为有耗介质，在计算区域内部设3个观察点，分别采用2种方法计算观察点的场值。FDTD剖分网格δ=8 mm，时间间隔Δt=0.005 ns，CPML吸收边界节点为：-43∶43（x方向）;-43∶43（y方向）;-83∶83（z方向），连接边界为：-53∶53（x方向）;-53∶53（y方向）-93∶93（z方向）。3个观察点坐标分别为EP1（0 m，0.16 m，0.16 m），EP2（0 m，-0.16 m，0.16 m），EP3（0 m，0 m，0.16 m），图6（a）和图6（b）分别给出采用传统半空间FDTD方法和文中方法的计算结果及文中方法相比于传统方法的计算误差。

由图6可见，2种方法结果吻合较好，相比于传统方法，文中方法的计算误差在0.5%之内，证明了文中方法的正确性。根据FDTD计算中的Courant stability condition，可对三维FDTD迭代所需计算内存及时间步数进行估算[24]。以算例3中目标为例，采用传统半空间FDTD方法和文中方法所需要的内存及时间对比情况见表1.

由表1可见，文中方法在计算内存和时间上均具有明显的优势。在当前计算参数下，文中方法所需计算内存及时间分别减少到传统方法的52%和56%，且该优势会随着目标电尺寸的增大及目标距地面高度的升高而愈加明显。

2.2 有耗半空间上方金属腔时域的屏蔽效能

通常电子或电气设备会对3类物理量敏感：电场或磁场瞬时响应的最大值、磁通或电通密度随时间变化引起的感应效应最大值、和传输到器件上的总能量。依据不同的敏感类型，时域SE有3种不同的定义[26]：峰值下降（peak value reduction，PR）屏蔽效能、导数下降（derivative reduction，DR）屏蔽效能和能量密度下降（energy density reduction，ER）屏蔽效能。

式中 E0-max和Es-max分别表示屏蔽腔不存在和存在时空间某个位置电场瞬时最大值，

E·0-max

和

E·s-max

分别表示屏蔽腔不存在和存在时空间某个

位置电场变化率的最大绝对值，

W0和Ws分别表示屏蔽腔不存在和存在时观察点的能量流密度。

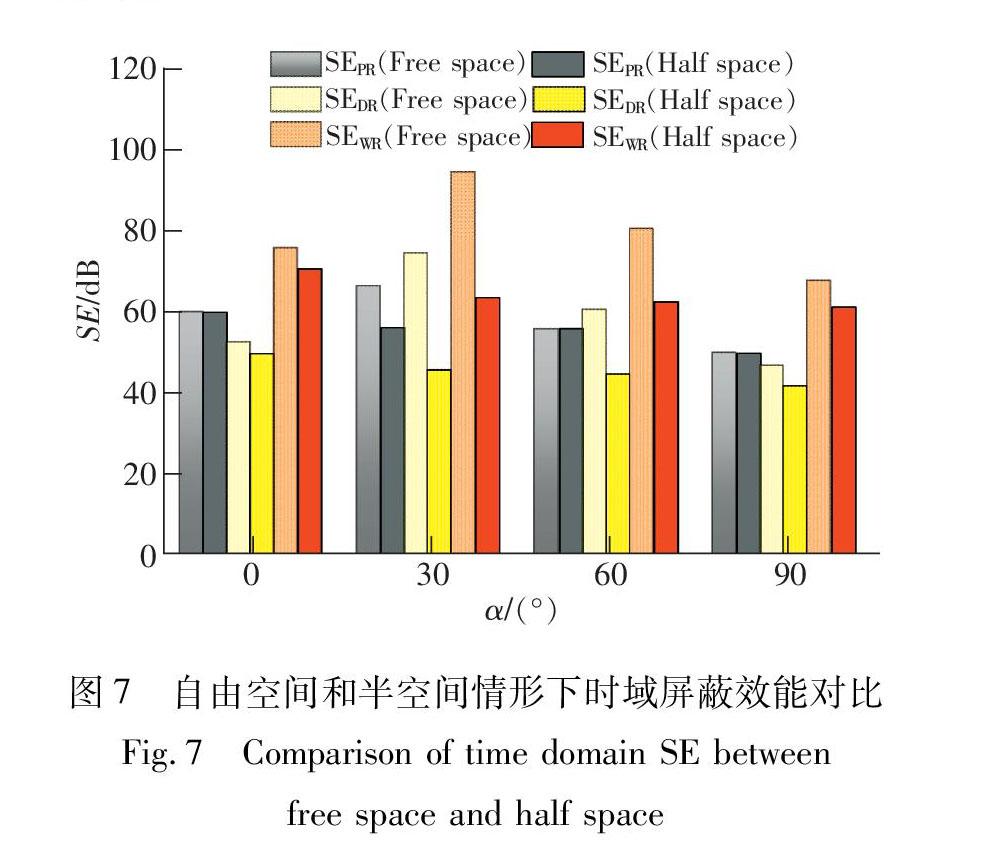
根据（5）式，可计算出（4）式照射下有耗半空间（εr=3，σ=0.1 S/m）上方腔体的时域屏蔽效能。图7给出不同极化角的入射波照射下，自由空间和半空间情形腔体中心3种时域屏蔽效能的对比情况。

由图7可见，由于SEPR计算的根据观察点瞬态场的最大值进行计算得到的，而通常反射波的幅值小于直接入射波幅值，因此半空间环境下的SEPR保持与自由空间相同的变化趋势;而SEDR，SEWR与自由空间相比均有所下降，下降的幅度在α0=30°达到最大。由此可见，由于半空间的存在，界面反射波给目标新一轮的冲击，造成屏蔽腔的屏蔽效能下降。

3 结 论

针对现有方法计算效率不高的问题，提出了一种无需使用半空间格林函数的改进半空间FDTD方法，实现了半空间上方金属屏蔽腔内场强分布及时域屏蔽效能的快速计算。由于半空间的存在，细缝屏蔽腔的时域屏蔽效能显著下降。由于文中方法无需求解形式复杂、计算困难的半空间格林函数，可方便地应用在复杂半空间及其上方目标的复合电磁问题中。

参考文献（References）：

[1] IEEE Standard method for measuring the effectiveness of electromagnetic shielding enclosures[S].IEEE Stanstard，IEEE，2007.

[2]SHOURVARZI A，JOODAKI M.Shielding effectiveness measurement for extremely small dimension enclosures[J].IEEE Transactions on Electromagnetic Compatibility，2019，61（6）：1740-1745.

[3]安靜，吴敏，高建强，等.金属腔体多耦合通道电磁特性研究[J].微波学报，2019，35（5）：63-66.AN Jing，WU Min，GAO Jian-qiang，et al.Study on electromagnetic characteristics of multi-coupling channels for the metal cavity[J].Journal of Microwaves，2019，35（5）：63-66.

[4]CELOZZI S，ARANEO R，Lovat G.Electromagnetic shielding[M].Hoboken，NJ，USA：Wiley，2008.

[5]周澤伦.带孔缝箱体电磁屏蔽效能的研究[J].西安科技大学学报，2016，36（1）：122-126.ZHOU Ze-lun.Research on the shielding effectiveness of the box with apertures[J].Journal of Xian University of Science and Technology，2016，36（1）：122-126.

[6]CERRI G，DE L R，PRIMIANI V M.Theoretical and experimental evaluation of the electromagnetic radiation from apertures in shielded enclosures[J].IEEE Transactions on Electromagnetic Compatibility，1992，34（4）：423-432.

[7]ARANEO R，LOVAT G.Fast MoM analysis of the shielding effectiveness of rectangular enclosures with apertures，metal plates，and conducting objects[J].IEEE Transactions on Electromagnetic Compatibility，2009，51（2）：274-283.

[8]杨福荣，李鹏，许万业，等.线缆-机箱电磁兼容分析的PEEC-MoM混合方法[J].西安电子科技大学学报，2016，43（6）：147-152.YANG Fu-rong，LI Peng，XU Wan-ye，et al.PEEC-MoM hybrid method for electromagnetic compatibility analysis of the cable-enclosure system[J].Journal of Xidian University，2016，43（6）：147-152.

[9]MAI H X，CHEN J，ZHANG A X.A hybrid algorithm based on FDTD and HIE-FDTD methods for simulating shielding enclosure[J].IEEE Transactions on Electromagnetic Compatibility，2018，60（5）：1393-1399.

[10]李俊辛，张晓萍，闫丽萍，等.基于JASMIN的并行CP-FDTD建模与屏蔽效能评估应用[J].强激光与粒子束，2019，31（5）：42-48.LI Jun-xin，ZHANG Xiao-ping，YAN Li-ping，et al.JASMIN-based parallel CP-FDTD modeling and application to shielding effectiveness prediction[J].High Power Laser and Particle Beams，2019，31（5）：42-48.

[11]周平.TSF算法及其在机箱屏蔽效应分析中的应用[J].西安科技大学学报，2006，26（2）：259-262.ZHOU Ping.TSF algorithm for analysis of the effect of a shielding box[J].Journal of Xian University of Science and Technology，2006，26（2）：259-262.

[12]CHEN J，GUO J Y，TIAN C M.Analyzing the shielding effectiveness of a graphene-coated shielding sheet by using the HIE-FDTD method[J].IEEE Transactions on Electromagnetic Compatibility，2018，60（2）：362-367.

[13]CARPES W P，PICHON L，RAZEK A.Analysis of the coupling of an incident wave with a wire inside a cavity using an FEM in frequency and time domains[J].IEEE Transactions on Electromagnetic Compatibility，2002，44（3）：470-475.

[14]BENHASSINE S，PINCHON L，TABBARA W.An efficient finite-element time-domain method for the analysis of the coupling between wave and shielded enclosure[J].IEEE Transactions on Magnetics，2002，38（2）：709-712.

[15]LUO W，LIAO Y，ZHAO Z G，et al.Accurate simulation of shielding effectiveness of metallic cabins using an improved calderon preconditioner-based time-domain integral equation method[J].IEEE Transactions on Electromagnetic Compatibility，2019，60（1）：200-208.

[16]NIE B L，DU P A，YU Y T，et al.Study of the shielding properties of enclosures with apertures at higher frequencies using the transmission-line modeling method[J].IEEE Transactions on Electromagnetic Compatibility，2011，53（1）：73-81.

[17]MOLLER C，KLINKENBUSCH L.Electromagnetic and transient shielding effectiveness for near-field sources[J].Advances in Radio Science，2007（5）：57-62.

[18]CELOZZI S，ARANEO R.Alternative definitions for the time-domain shielding effectiveness of enclosures[J].IEEE Transactions on Electromagnetic Compatibility，2014，56（2）：482-485.

[19]ARANEO R，CELOZZI S.Toward a definition of the shielding effectiveness in the time-domain[J].IEEE International Symposium on Electromagnetic Compatibility，2013，5（9）：113-117.

[20]曹樂，魏兵，朱湘琴.高功率微波照射下半空间上方天线罩耦合特性[J].强激光与粒子束，2015，27（8）：136-141.CAO Le，WEI Bing，ZHU Xiang-qin.Electromagnetic energy coupling analysis of radome over lossy half space under High Power Microwave[J].High Power Laser and Particle Beams，2015，27（8）：136-141.

[21]綦鑫，聂在平，阙肖峰，等.半空间环境下跨界金属目标电磁散射快速分析研究[J].电子科技大学学报，2018，47（4）：521-525.QI Xin，NIE Zai-ping，QUE Xiao-feng，et al.Fast analysis of EM scattering from PEC bodies straddling a half-space interface[J].Journal of University of Electronic Science and Technology of China，2018，47（4）：521-525.

[22]NAZARI M E，HUANG W M.An analytical solution of electromagnetic radiation of a vertical dipole over a layered half-space[J].IEEE Transactions on Antennas and Propagation，2020，68（2）：1181-1185.

[23]CHEW W C.Waves and fields in inhomogeneous media[M].New York：Van Nostrand Reinhold，1990.

[24]葛德彪，闫玉波.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社，2011.

[25]TAFLOVE A，HAGNESS S C.Computational electrodynamics：the finite-difference time-domain method[M].Norwood，MA：Artech House，2005.

[26]CELOZZI S.ARANEO R.Alternative definitions for the time-domain shielding effectiveness of enclosures[J].IEEE Transactions on Electromagnetic Compatibility，2014，56（2）：482-485.