改进平滑A*算法的多AGV路径规划

胡蔚旻，靳文舟

华南理工大学 土木与交通学院，广州 510461

1 引言

随着科技的发展，机器人逐渐替代人工搬运，自动导引车（Automated Guided Vehicle，AGV）因其具有任务执行、精确定位、环保高效、智能运作等特点被广泛使用，尤其在货物运输领域[1]，被公认为是实现物流运输的最佳之选[2]。AGV 系统可通过控制平台实现对各AGV运行状况、地理定位、任务派遣的监控与更改，具有投资小、占地少、搭建周期短、安全、便捷等特点[3]，若将其合理地运用于车间物流运输，通过科学地改进线路算法与系统协调策略，能够有效地减少人力需求，极大提高生产工作效率，降低生产损耗与成本。

秦珅等[4]利用双向同步A*算法实现路径起终点同步搜索，以提高路径规划效率。李强等[5]通过引入象限概念，筛选、剔除无效拓展备选点，实现搜索效率的提高，但是由于约束条件限制，只搜索与目标点同象限位置的拓展点，导致该方法的普适性大幅降低。王子意[6]通过区分AGV直行、转弯速度将路径转弯列入A*算法估计函数，利用实例证明在一定环境下单AGV 线路可减少超60%转向次数。

上述方法大多针对单AGV 情况，由于运输路网为多台AGV共用，运行期间将存在线路间的时空冲突，需制定相应的协调策略避免车辆间碰撞、死锁等冲突现象的发生。常见算法有 A*算法[7]、遗传算法[8]、Dijkstra 算法[6]、人工势场法[9-11]等。Draganjac 等[12]通过对低优先级的车辆采用等待或者移除的策略解决路径冲突。Banaszak等[13]提出资源共享和流量排序的协调策略，以解决动态环境中的冲突、死锁等现象。袁洋等[14]通过引入负载量优化A*算法，实现路网的负载均衡，有效降低AGV发生冲突的概率，提高系统工作效率。贺丽娜[15]通过将时间窗原理引入Dijkstra 算法实现多AGV 无碰撞路线规划，结合实例证明了引入时间窗的有效性。许伦辉等[16]以下达任务的时间先后顺序降序设置优先级，并以优先级从低至高依次对冲突路径进行协调，此方案能够有效消除路网中所有冲突，但仅以下达任务时间作为线路协调顺序标准，易导致系统完成所有任务的所需总时长大幅增加。

基于此，本文依据路网及车辆行驶特性，构建笛卡尔坐标系环境；通过提出一种以3轴-2象限为筛选约束的改进A*算法，在保证普适性的前提下通过约束条件剔除无效搜索点，达到提高搜索效率的目的，并引入转向数指标优化路径平滑度；以改进算法为基础，结合所建环境，对车辆冲突类型、判别进行量化分类，借鉴时间窗原理，以系统总工作时长最短为原则制定相应的协调策略，寻求系统运行效率最佳。

2 构建坐标系地图模型

栅格法由Howden 提出[17]，利用单位栅格对地图进行划分，结合灰度值区分自由、障碍栅格，栅格的大小对精度具有决定性作用，缩小栅格能够提高精度，但会导致地图的信息量呈几何式增长[18]，从而降低路径规划效率。基于栅格法思想，结合AGV运行线路的正交性、定位精准性，构建改进笛卡尔坐标系地图模型作为规划环境，即以笛卡尔坐标系第一象限作为电子地图，利用二维坐标完成AGV 运行的精确定位，此地图模型还能满足线路的正交性、路径长度便捷计算等要求。

3 改进A*算法

3.1 提高搜索效率

传统A*算法是以当前所在点为中心，对其各方向上限定范围内的点作为拓展备选点进行遍历，本质与八码数问题相同。目前AGV 运行路径多为正交线路，基于坐标系地图，若以八码数遍历原则进行路径规划，则会导致对角线上的4 个无效点（图1）仍然会进行先运算、再剔除的无效运算过程，从而降低规划效率。

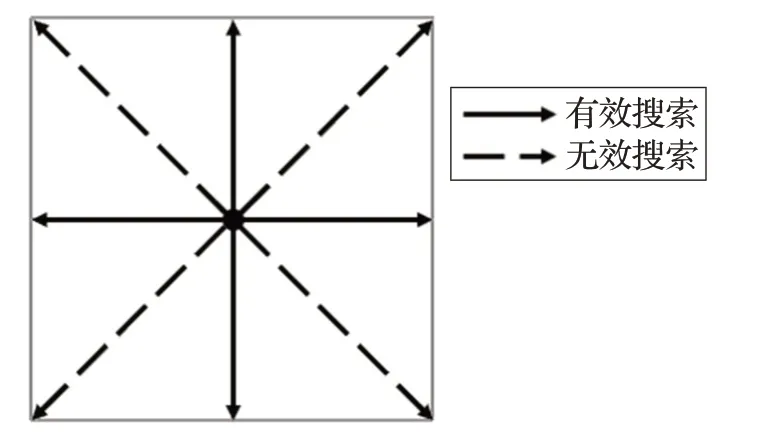
图1 传统A*算法拓展备选点示意图

李强等[5]通过引入象限概念筛选拓展备选点，但由于只选取与目标同象限的周边点，导致其适用范围有所限制。鉴于此，本文提出正负象限概念，构建3 轴-2 象限搜索法实现拓展备选点的筛选，即以当前点为次坐标轴原点建立x′y′正交坐标系，4个半轴上单位长度定点为搜寻备选集（图2），依据式（1）～（3）确定目标点与当前点的正负象限关系，剔除无效搜索轴，完成备选点筛选。

图2 双坐标系

其中，(xs,ys)表示起点S坐标，(xe,ye)表示目标点E坐标，Cx、Cy为常数。

3.2 优化路径平滑度

AGV 运行时因转向产生的延误将降低工作效率，过于频繁地转向还会加速机器的损耗，缩短使用寿命。为了提高使用效率，减小与实际运行的误差，将路径转向数引入算法估价函数，通过减少转向数，获取平滑路径，提升运行效率。改进后A*算法的估计函数如下：

其中，f(m)是扩展节点到目标点的估价函数，g(m)表示扩展节点M至起点的实际代价，g(x)为扩展节点到起点的已知成本[19]，σ表示转向数转换为成本代价的换算系数，为第k辆AGV 扩展节点M的坐标。由于行驶路径的正交性，可选用曼哈顿距离作为启发函数h(m) 的估计代价，如式（10）。表示第k辆AGV目标点E的坐标。改进后A*算法流程如图3。

4 多AGV协调

为进一步提高工作效率，建立基于时间窗法的路径协调模型，消除各路径间潜在冲突，实现多AGV的路网时空共用，以提高系统运行效率。本文基于此思想，细化空间冲突类型划分，明确类型量化判别，通过多协调方式比对择优，实现系统工作效率最优。

4.1 冲突分类、判别

AGV冲突可划分为空间冲突、空间无冲突、时间无冲突三类。

空间冲突可细分为节点冲突（图4（a））和路段冲突，其中路段冲突分为对向冲突（图4（b））和同向冲突（图4（c））。

空间无冲突表示不同AGV规划线路在空间上不存在重叠现象，即可独立运行、互不影响、无须协调。

时间无冲突表示不同AGV 路径可能存在空间重叠，但时间不重叠，此类冲突中不同AGV虽然共用同一路段，但在时间维度为错位重叠，因此互不产生影响，仍可独立运行，无须协调。

图3 改进A*算法流程图

图4 AGV冲突

冲突判别方式如下：

其中，T为任务执行时刻集，tN表示第N辆AGV在tN时刻开始执行任务，AGVN为第N辆AGV的路径集，Nn表示第N辆AGV在n时刻的节点坐标位置。

4.2 协调策略

对于节点冲突采用二者依次等待让行策略，路段冲突则细分为两类进行讨论：

若到达冲突起点的AGV存在时间错位，但因错位不足而产生冲突，采用先到先通行，后到等待让行的策略。

若存在冲突的AGV 同时到达冲突路段起点，采用二者依次等待让行、重新规划路径以最小工作总时长为指标的多协调方案比对择优策略。此方法与目前多数以优先度为指标，单一重新规划低优先度的车辆路径的协调策略相比，排除了主观因素对制定优先度的影响。

出于安全考虑，存在冲突的AGV 间需等优先使用路段的AGV 完全通过后方可继续使用，等待时间计算如下：

其中，lroadr表示路段r的长度，lAGVn表示第n辆AGV的长度，vAGVn为第n辆AGV的行驶速度。

5 评价指标

5.1 算法评价

5.1.1 路径总长L

AGV 运行效率大多采用路径总长度作为评价指标，由于车辆转向产生时间延误，一些学者还将工作时长作为辅助评价指标。本文引入转向数对A*算法的估价函数进行优化，车辆在路径选择时已考虑转向造成的延误，无须另外增设时间评价指标，因此选用各AGV规划路径总长度作为规划方法优劣的评价指标。

5.1.2 备选点数P

对于相同的路网环境、任务起终点，同一评价体系下采用不同规划方法存在获取相同且最优的规划路径的现象，因此选用方法的运行效率成为系统工作效率的决定因素。路径规划时需对当前点进行多向拓展确定备选点并择优确定拓展点，拓展备选点的总数量可反映规划方法的工作效率，因此选取完成系统规划任务所需的拓展备选点总数作为系统运行效率的评价指标。

5.1.3 路径转向数TN

具有不同转弯数的规划路径即使线路长度一致，所需的实际运行时长也会存在差异，转弯数过多则会导致与预测值相差悬殊，从而降低规划精度。为提高规划可行性、可靠性，缩小与实际差值，将路径转弯数列入评价指标体系。

5.2 协调策略评价

由于一个系统中存在AGV 间的冲突协调、转向时间延误等，仅通过系统路径总长度无法达到对效率的有效评价，而整个系统完成任务所需的总时间则能较好地反映工作效率。

6 实例分析

构建图5所示具有障碍物的30 m×30 m坐标系地图模型作为规划环境（×表示障碍物，下同），以X=1 为任务起点线，X=30 为任务目标点线。随机产生5个搬运任务，每个任务由一台AGV 独自完成，每台AGV 车身长度lAGVn为1 m，行驶速度vAGVn为0.5 m/s，每个转向延误时长3 s。各搬运任务信息及运行结果如表1和表2。

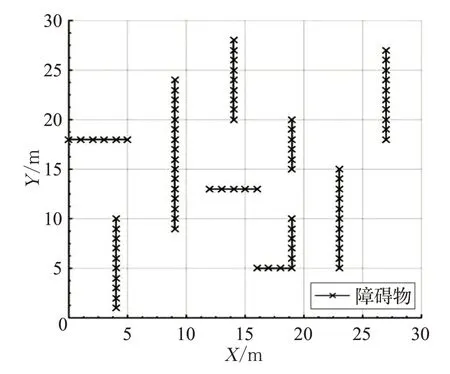
图5 规划环境

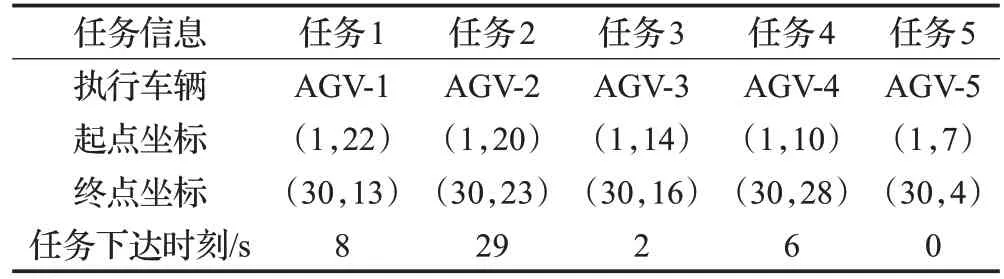
表1 任务信息

表2 运行结果

依据表2 可知，采用欧几里德距离、曼哈顿距离作为启发函数均可获得相同且最短的规划路径；无论启发函数是欧氏距离，还是曼氏距离，采用传统4 轴搜索法的遍历点数均少于3轴-2象限搜索法；以相同搜索法为前提，曼氏距离作为启发函数的搜索点均少于欧式距离，证明了3 轴-2 象限搜索法、曼哈顿距离启发函数的合理性、有效性。因此采用3 轴-2 象限搜索法，以曼氏距离为估价函数的A*算法作为AGV路径规划原则。

为进一步提高规划精度，缩小与实际运行的误差，将行驶转向数1-cos引入成本函数参数集进行路径规划，结果如表3所示。

表3 规划路径详情

由于拓展节点时考虑了转向所产生的附加成本，在获取相同最短路径长度的前提下，上述A*算法更偏向于择取产生转向数较少的节点进行拓展。依据表中数据可知，基于上述A*算法并考虑转向数的改进A*算法能显著缩减行驶路径的转向次数，降低因转向产生的附加延误，从而缩小与实际运行间的误差。其中任务3由于已为最短路径下最少转向方案，增设转向数参数后的规划方案仍为最短路径的最少转向路径。采用改进A*算法对上述搬运任务进行路径规划，结果如图6所示。

由图6 可知，系统工作总时长为 123 s（AGV-2 所对应的任务2），存在空间冲突的路段如表4所示。

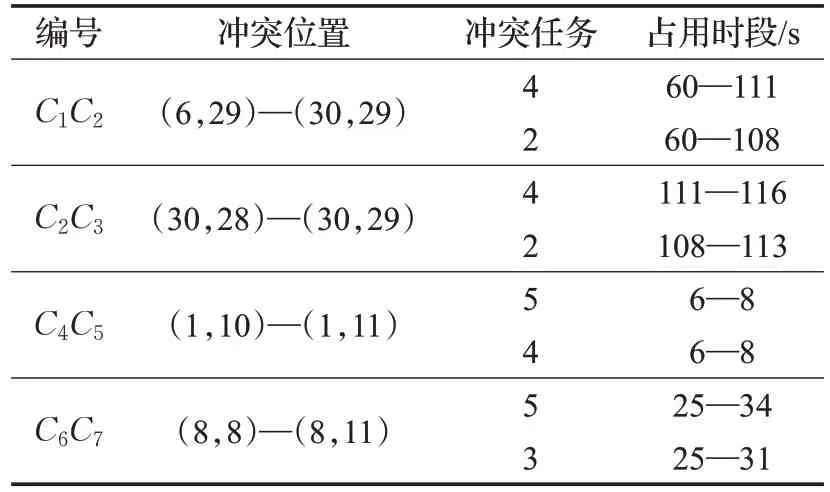
表4 冲突路段详情信息

图6 （a）规划线路结果

图6 （b）规划线路（X 轴）-时间图

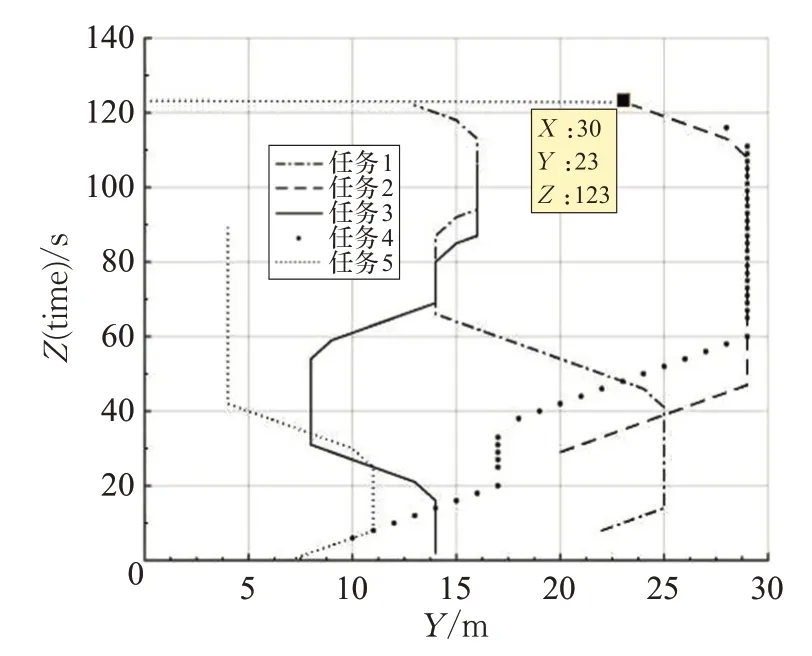
图6 （c）规划线路（Y 轴）-时间图

路段C4C5起始端点为任务4 的起点，因此选用AGV-5等待让行的协调策略，等待时长为2 s；由于时间延长的传递性，AGV-5 到达路段E的时间延长至26 s，较AGV-3推迟2 s到达，则继续选取AGV-5等待让行的协调策略，等待时长为2 s；AGV-2和AGV-4均在58 s到达路段A 起始端点，则分别对两台AGV 进行路线重规（图7、图8，为便于观察，图中仅显示AVG-2/4线路）、等待让行，进而择优选取协调方案。

（1）AGV-2路线重规

AGV-4仍按原规划线路行驶，AGV-2则将路段A视为障碍物后进行路径重新规划，如图7，重规后的路径长度增加2 m，转向数增加2个，但避免了因冲突而产生的等待延误，AGV-2、AGV-4工作总时长分别为133 s、116 s，系统工作总时长为133 s（AGV-2所对应的任务2）。

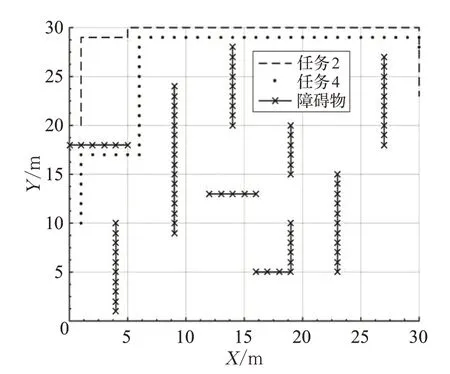
图7 （a）AGV-2重规线路图

图7 （b）AGV-2重规线路（X 轴）-时间图

图7 （c）AGV-2重规线路（Y 轴）-时间图

（2）AGV-4路线重规

AGV-2仍按原规划线路行驶，AGV-4则将路段A视为障碍物后进行路径重新规划，如图8，重规前后的路径长度不变，转向数略有增加，AGV-2、AGV-4工作总时长分别为123 s、122 s，系统工作总时长为123 s（AGV-2所对应的任务2）。

（3）AGV-2等待让行

AGV-2在冲突路段A 起始端点处等待AGV-4完全通过后方可通行，等待时长为4 s，则AGV-2、AGV-4 工作总时长分别为127 s、116 s，系统工作总时长为127 s（AGV-2所对应的任务2）。

图8 （a）AGV-4重规线路图

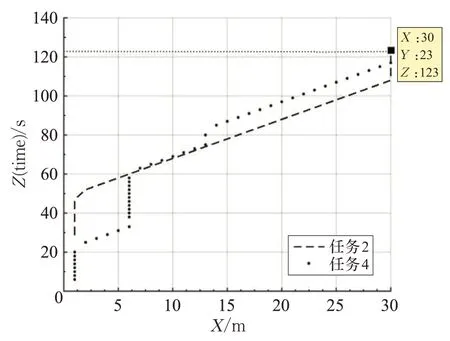
图8 （b）AGV-4重规线路（X 轴）-时间图

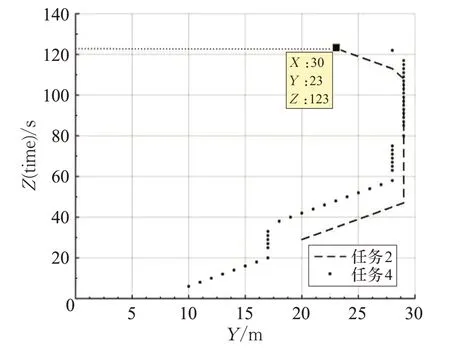
图8 （c）AGV-4重规线路（Y 轴）-时间图

（4）AGV-4等待让行

AGV-4在冲突路段A 起始端点处等待AGV-2完全通过后方可通行，等待时长为4 s，则AGV-2、AGV-4 工作总时长分别为123 s、120 s，系统工作总时长为123 s（AGV-2所对应的任务2）。

通过方案比对可知，4 种冲突协调方案中对AGV-2采取等待让行、路线重规均会导致系统工作总时长的增加，分别为4 s、10 s；对AGV-4 采取等待让行、路线重规不改变系统工作总时长且二者所需的时间总长一致，即均为123 s。前者利用时间错位避免冲突，但仍存在较长的空间冲突，一旦处于时间维度前期的车辆在重叠路段上出现故障，将会影响后期使用该路段的所有车辆。若假设车辆发生故障的概率呈随机分布，则存在空间冲突的路段长度与发生上述情况的概率为正相关，因此针对本系统任务，择优选择AGV-4路线重规的协调策略。若借鉴先到先服务的原则，依据下达任务的时间先后顺序，仅对后者AGV采取等待让行或线路重规策略，将增加系统运输总时，降低工作效率。

7 结束语

本文通过结合AGV 路径特征建立坐标系环境，并引入3 轴-2 象限概念及转向数实现对传统A*算法的改进，以系统总时最小为目标，借鉴时间窗原理制定多AGV冲突判别、协调策略。通过实例证实，改进的方法不仅大幅减少拓展备选点数和转向数，提高路径规划效率，还能保证协调结果达到系统最佳，避免因追寻某一任务最短用时而陷入系统局部最优的现象。

本文算法在速度、规划效果上均有所优化，但在动态鲁棒性上尚未改进，针对车辆故障等突发情况，整体路网如何进行动态实时调整可后续深入研究。