改进非对称相似度和关联正则化的推荐算法
2020-08-19刘春玲
刘春玲,张 黎
武汉纺织大学 机械工程与自动化学院,武汉 430200
1 引言
随着信息技术和互联网的发展,人们逐渐进入信息爆炸的时代,如何从海量信息中快速获取相关的信息已成为亟待解决的问题。推荐系统作为一种有效的信息过滤技术,是解决这一问题的重要手段,在各大电商平台、音乐网站以及在线评论网站中有着广泛的应用[1]。推荐系统通过分析用户历史行为(如评分、浏览记录等),来预测用户在不同项目上的兴趣偏好,从而帮助用户快速有效地获取其需要或感兴趣的项目。随着推荐系统的发展,各类相关理论与技术应运而生,目前应用最广泛、效果较好的是协同过滤(Collaborative Filtering)推荐算法。
协同过滤推荐算法[2-5]根据用户的行为来分析用户偏好,根据推测结果给出相关推荐内容,其中又以矩阵分解应用较广。苏庆等[6]考虑时间差因子、热门物品权重因子以及冷门物品权重因子,提出一种改进模糊划分聚类的协同过滤推荐算法。黄贤英等[7]考虑了用户关系的不平衡性,提出一种改进用户非对称相似性的协同过滤推荐算法。Salakhutdinov等[8]从概率的角度解释了传统矩阵分解模型的合理性,并提出了概率矩阵分解模型(Probabilistic Matrix Factorization,PMF)。Saveski 等[9]融合项目内容信息和用户历史行为提出一种LCE(Local Collective Embeddings)算法,有效缓解了冷启动问题。
融合用户信息与矩阵分解的推荐算法在一定情况下行之有效,但仍受限于数据稀疏的问题,难以解决冷启动问题,为此研究者们提出了社会化的推荐算法。为了平衡用户间信息的不对称性,Ma 等[10]考虑了用户的社会信息,提出SoRec推荐算法。吴宾等[11]不仅考虑了用户的社会信息,还将用户的关联关系作为考量因素,提出联合正则化的矩阵分解算法。Guo 等[12]在SVD++模型的基础上考虑用户之间的显式信任信息加入评分预测,通过用户之间的信任关系对特征向量进行学习。Yang等[13]综合考虑信任者和被信任者模型,提出了一种混合推荐算法TrustMF。Jamali 等[14]运用信任传播方法,提出SocialMF,有效缓解了冷启动问题。郭宁宁等[15]提出了一种融合社交网络特征的协同过滤推荐算法,有效缓解了数据稀疏性对推荐结果的影响,并提高了推荐准确率。但以上算法的社会关系或者信任关系是显式的,信息只能通过用户标注来获取。
针对上述算法存在的问题,本文提出一种改进非对称相似度比和关联正则化的推荐算法。考虑不同用户与不同项目之间的不对称关系,提出一种改进相关度计算式,在综合考量项目与用户两种不同因素偏移量的补充量的基础上,对评分预测式加以改进。同时针对用户历史行为信息不对称的问题,利用传统相似度获取邻域集合来表示用户的社会关系,将关联正则化用于约束矩阵分解目标函数,以此缓解数据稀疏带来的用户信息不对称。实验结果表明,与主流的推荐算法相比,该算法能够更加有效地预测实际评分。
2 矩阵分解推荐算法
2.1 传统矩阵分解推荐算法
一般来说,用户在评分的时候会有个人偏好,有的用户评分普遍比其他用户高,有的用户则普遍偏低,因此,一般定义基础偏移量bui来表示用户和物品的偏好。

其中,表示所有评分的平均值,bu表示用户u的评分偏好,bi表示用户对项目i的评分偏好。例如小明给电影《魔戒》打分,《魔戒》的平均分为3.5 分,高一般电影1.0 分,小明给电影的平均评分高一般用户0.1 分,则bui=3.5+1.0+0.1=4.6。
传统的矩阵分解将预测评分矩阵∈Rm×n分解为用户特征矩阵P∈Rm×k和项目特征矩阵Q∈Rk×m,其中k为特征个数。其用户的评分预测计算式见式(2):

其中,pfu表示用户u的第f个特征值,qfi表示项目i的第f个特征值。为了提高预测精度,需要使得预测值与真实值之间的差值最小,目标函数G见式(3):

其中,λ为正则项系数,为正则项,用于防止在训练中出现过拟合。以bu为例,如果不增加正则项,在训练参数时,参数迭代式为在增加正则项后,参数迭代式变为bu=(1-λα)bu-显然1-λα小于1,实现了权重衰减,也减少了训练中出现过拟合的可能。
2.2 改进用户非对称性的矩阵分解推荐算法
实际情况中,不同用户之间的评分数量存在较大差异,因此其潜在特征向量的样本数也是不同的。对于这一情况,传统的矩阵分解算法未予以考虑。黄贤英等[7]考虑了用户关系的不平衡性,对评分预测式做出了一些改进,具体见式(4):
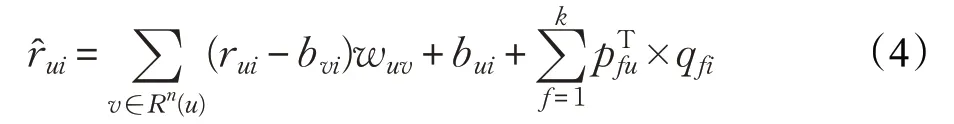
其中,wuv表示用户u和用户v之间的评分关系,作为bu偏移项,是对基础偏移量的补充。当wuv和rui-bui较高时,说明预测值要低于实际值,此时正好可以补充预测值,使其更接近实际值。Rn(u)表示用户u的前n个近邻,可以由wuv得到:

其中,N(u)表示用户u有过评分的项目数,N(v)表示用户v有过评分的项目数。基于用户非对称性的矩阵分解推荐算法的目标函数见式(6):
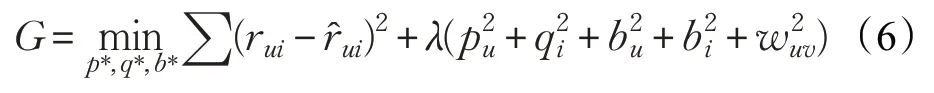
上述目标函数考虑了用户之间的相关性,对于行为信息少的用户,利用其邻居的行为进行补充和修正,在一定程度上克服了数据稀疏的问题。然而,在海量用户与项目数据并存的背景下,仅考虑用户信息而未考虑项目变化的模型就显得较为单一,其忽略了项目的关联变化会影响用户之间关系的因素,容易造成数据稀疏问题,降低了算法推荐的准确度。
3 基于非对称相似度和关联正则化的推荐算法
3.1 基于非对称相似度的矩阵分解推荐算法
基于用户非对称性的矩阵分解推荐算法仅考虑用户之间的相关性,然而不同项目之间的相关性程度也可能影响用户对项目的评分,因此本文在深入研究项目之间联系的基础上,通过综合用户信息、项目变化以及两者之间的关系来对原模型进行补充改进。具体做法为基于项目的关系在原模型的基础上增加一个偏差量用于补充项目偏差量,式(4)和式(6)分别变为了式(7)和式(8):
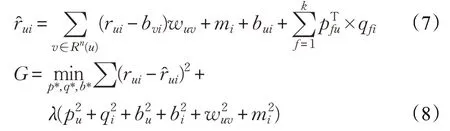
其中,mi是bi的偏移量,与wuv的作用相似,是对基础偏移量的补充,如果用户u喜欢的项目都与项目i的相关性很高,可以使用mij对预测值进行修正(补充),反之如果用户u喜欢的项目与项目i的相关度不高,那么使用mij对预测值进行修正(减少)。以电影推荐为例,如果用户u看过《加勒比海盗》1~3部,那么在预测其对《加勒比海盗》第4 部的偏好时会给予增量,而如果用户u没有看过加勒比系列相关电影,那么在预测其对《加勒比海盗》第4部的偏好时会给予惩罚。其具体定义见式(9):

其中,cij表示项目i和项目j之间的相似度,μi表示第i个项目和其他所有项目相似度的均值,Rn表示所有项目。
同样以电影推荐为例,在实际推荐中,如果用户经常看高分电影,则该类型用户在较小可能性下会去看低分电影。基于该种情况,本文参考用户相似度的定义,在衡量项目相似度的同时综合考虑不同项目的评分情况以及共现次数,以此提出一种改进项目相似度cij计算式。其定义见式(10):
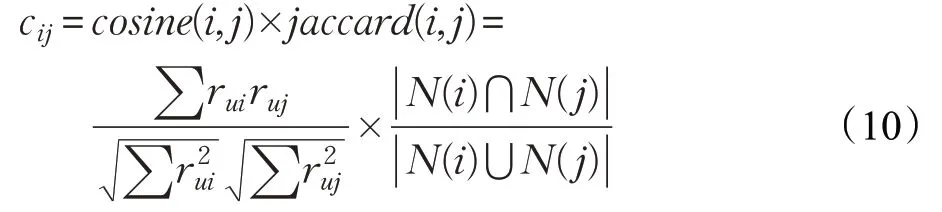
其中,N(i)表示项目i有过评分的数量,N(j)表示项目j有过评分的数量。cosine(i,j)从评分角度衡量两个项目之间的相关性,jaccard(i,j)是从共现次数角度评价两个项目之间的共现。再以电影推荐为例,如果项目i和j分别是热度很高的高分电影和低分电影,那么jaccard(i,j)会较为相似,但是cosine(i,j)会很大区别;而如果项目i和j分别是一个喜剧低分电影和一个恐怖低分电影,其cosine(i,j)会较为相似,而jaccard(i,j)区别会很大,因此式(7)可以较好地区分不同类型的电影以及相同热度下不同口碑的电影。
3.2 基于非对称相似度和关联正则化的推荐算法
社会学研究发现,同一社群的用户偏好存在较大的相似性。由Ma 等的研究可知,将社会正则化作为矩阵分解的约束可以提高矩阵分解推荐算法的效果。然而基于社会正则化的矩阵分解推荐算法一般根据用户的社会关系,这需要用户给出其信任用户群,是一种显式表示。而由于涉及隐私,通常用户不会直接给出完整的信任用户群,因此本文采用一种隐式表示法,将用户的近邻用户集作为其信任用户群,在综合考虑不同用户与不同项目之间相关性的基础之上,提出一种基于非对称相似度和关联正则化的推荐算法。对此,在上文改进评分预测式的基础上将关联正则化作为矩阵分解的约束,一方面可以避免模型训练过程中出现过拟合;另一方面在模型中增加了用户信息,对于信息量很少的用户,其潜在特征向量会更接近于其近邻用户的特征向量,因此该类用户信息可以得到一定的补偿,对其进行评分预测时也能得到较高的评分预测精度。改进后的目标函数见式(11):

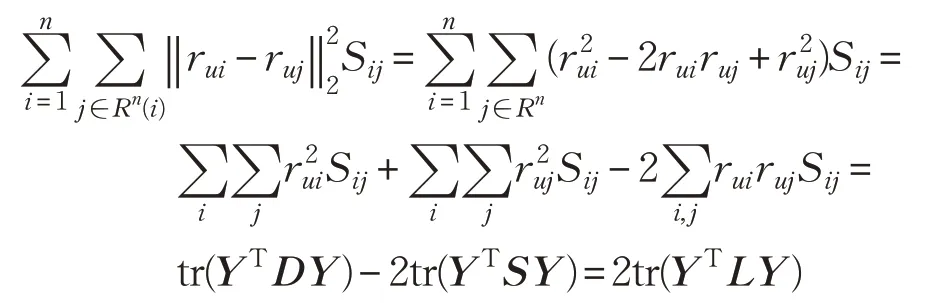
因此,式(11)变为式(12):

本文使用随机梯度下降来求解式(11),其核心操作在于计算梯度 ∂G/∂bu,∂G/∂bi,∂G/∂qi,∂G/∂pu,∂G/∂wuv,∂G/∂cij,如式(13)~(18)所示:


其中,eui表示预测评分和真实评分的差值。基于非对称相似度和关联正则化的推荐算法的时间复杂度主要包括了对目标函数G和各梯度的计算。计算目标函数G的时间复杂度为,其中|W|表示用户关联关系数量,表示项目关联关系数量,|R|表示评分数量,d表示特征空间的维度。计算梯度∂G/∂bu, ∂G/∂bi, ∂G/∂qi,∂G/∂pu, ∂G/∂wuv, ∂G/∂cij的时间复杂度,分别为可以看出该算法训练一轮的时间复杂度为,与用户关联关系数量、项目关联关系数量以及评分数量呈线性相关,可以处理大规模数据的推荐。
4 实验设计及结果分析
4.1 数据集及衡量标准
为了对比融合项目近邻和融合用户近邻的矩阵分解推荐算法在不同数据集上的表现,本文选取了Movie-Lens10M 数据集[16]、Amazon 评论数据集[17]以及 Ciao 数据集作为测试数据进行实验验证。三个数据集的评分范围均在[0,5],其统计特性见表1。
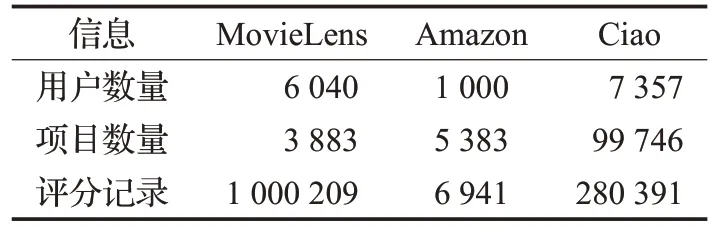
表1 三个数据集的统计特性
本文将数据集分成训练集和测试集,训练集用于训练推荐算法中的参数,测试集用于评估推荐算法的准确性,本实验按照9∶1的比例将数据集随机分割成训练集和测试集,实验程序基于Python语言实现。
本文选择了RMSE(Root Mean Square Error)作为衡量标准,通过计算预测评分和实际评分的均方根误差来描述算法的推荐质量,RMSE值越小说明推荐的质量越好。RMSE的计算公式见式(19):
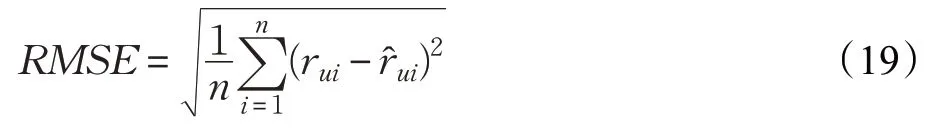
其中,rui为实际评分,为预测评分,n表示测试集中评分数量。
4.2 实验结果与分析
本文做了两组对比实验,实验1研究了本文算法在不同参数下的表现,实验2对比了本文模型和一些常用算法在真实数据集上的表现。
实验1 不同参数变化的效果对比
这部分实验都是在MovieLens数据集下完成。图1显示了随着迭代次数的增加,本文算法的RMSE 值变化,可以发现在迭代次数为50左右开始收敛。
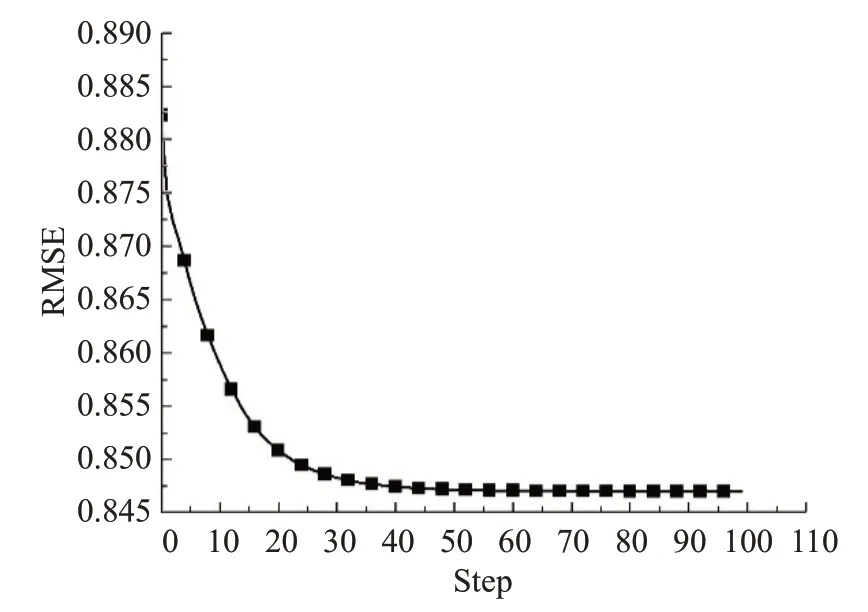
图1 本文算法在MoiveLens上的RMSE值
图2 显示了本文算法在不同邻居个数下的RMSE值变化。发现在低邻居个数的情况下,推荐效果逐步提升,但是在达到一定邻居个数之后,推荐效果出现了波动,可能出现一定程度的下降。

图2 不同邻居数下的RMSE值
图3 显示了本文算法在不同潜在特征维度下的RMSE值变化。发现在一定潜在特征维度下,算法的推荐效果逐步提升,但是在潜在特征维度达到一个特定值后,推荐算法效果近似收敛,无太大提升。

图3 不同潜在特征维度下的RMSE值
实验2 不同推荐算法的表现对比
表2是本文算法以及一些常用推荐算法在Amazon数据集以及MoiveLens 数据集上的RMSE 值。由实验数据可以看出,本文算法相较于其他算法在推荐准确性上有明显的提升,这是由于本文考虑了目标用户的关联用户信息。
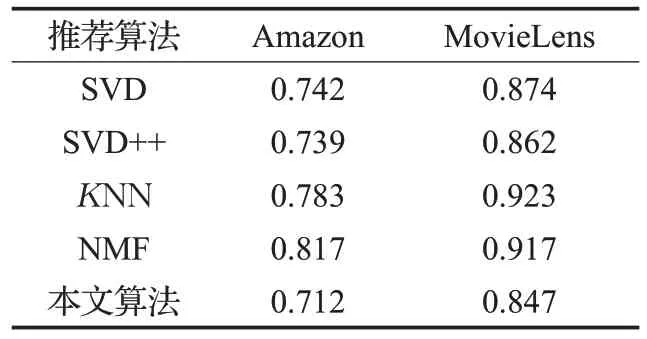
表2 本文算法和其他算法的RMSE值
在社会化推荐系统中考虑用户的信任关系通常可以提高推荐效果。为了进一步验证本文算法的推荐效果,本文还在Ciao数据集上进行了验证。表3显示了Ciao数据集的信任信息。从表3 和表1 的数据可以看出,信任关系的稀疏性要高于评分的稀疏性。

表3 Ciao数据集信任信息
表4对比了本文算法、SVD++算法以及现有的一些社会化推荐算法。从表4 可以看出,本文算法的RMSE值优于大部分基于社会关系的推荐算法,稍逊于trustSVD算法。而trustSVD 算法训练一轮的时间复杂度为,大于本文算法的时间复杂度,而且本文算法与后者算法的效果相比差别不大,因此综合来看,本文算法成本低,较容易实现。

表4 本文算法和其他算法在Ciao数据集上的RMSE值
5 结论
本文针对用户信息量不对称问题提出一种改进非对称相似度和关联正则化的推荐算法。考虑不同用户与不同项目之间的不对称关系,提出一种改进相关度计算式,在综合考量项目与用户两种不同因素偏移量的补充量的基础上,对评分预测式加以改进。同时针对用户历史行为信息不对称的问题,利用传统相似度获取邻域集合来表示用户的社会关系,将关联正则化用于约束矩阵分解目标函数,以此缓解数据稀疏带来的用户信息不对称。实验结果表明,与主流的推荐算法相比,该算法能够达到更好的推荐效果,同时与基于社会化的推荐系统相比,该算法的数据获取较为简单,推荐效果也有一定保证。
