基于改进FREAK的图像匹配算法
2020-08-19钱军浩王江文
黄 坤,钱军浩,王江文
(1.江南大学 物联网工程学院,江苏 无锡 214122; 2.西南交通大学 牵引动力国家重点实验室,成都 610031)
0 概述
图像匹配技术在计算机视觉领域得到广泛的应用。图像匹配可分为特征点检测、描述符生成和根据描述符进行匹配3个步骤[1-2]。提高图像匹配算法性能的关键在于生成区分度更高、运算量更小的描述符。因为二进制描述符表达紧凑且可利用位运算加速匹配,所以其所需的内存和运算量相比非二进制描述符大幅减小。近年来,研究人员提出了较多的二进制描述符算法。文献[3]提出一种ORB算法,该算法根据机器学习选择的点对生成二进制描述符,且引入方向信息使描述符具有旋转不变性。文献[4]提出一种BRISK(Binary Robust Invariant Scalable Keypoints)算法,该算法使用人为设计的采样模式,点对只在采样点里选取,大幅降低了训练点对时的复杂度。文献[5]基于BRISK算法固定采样模式的设计思想提出了一种FREAK算法,该算法借鉴视网膜视觉感知细胞的分布设计采样模式。借助设计合理的采样模式,FREAK算法在很多场合获得了优于其他二进制描述符的性能[6-8]。文献[9]提出一种CS-FREAK算法,该算法将FREAK算法的视网膜模型由8层简化为5层,然后增加中心对称采样点的领域强度信息。CS-FREAK算法的鲁棒性在FREAK算法的基础上有小幅改善,但是其描述符的计算和匹配过程更加复杂,实时性较低。文献[10]提出一种局部二值模式(Local Binary Patterns,LBP)图像特征点匹配算法,该算法不仅计算点对之间的差分大小关系,还计算点对与特征点之间的差分幅值关系来生成描述符。因为文献[10]算法同时利用了差分大小和差分幅值这2种信息,所以该算法具有很好的噪声抑制性能,但是其描述符长度较长且不具有旋转不变性。
为进一步提升图像匹配算法的实时性和鲁棒性,本文提出一种结合LBP和FREAK的联合特征匹配算法。根据文献[9]算法的思路简化FREAK视网膜模型,对简化后的模型通过机器学习算法选择高区分度、高非相关性的点对,在尽可能保证区分度的前提下减少点对数量以提高算法的实时性。在此基础上,设计一种具有旋转不变性的LBP对每个感受野进行编码,以提高描述符的区分度[11]。
1 FREAK 描述符
1.1 视网膜采样模型
FREAK 算法采用视网膜模型[5],该模型根据采样点距特征点的距离决定采样点的密度和高斯平滑内核。如图1所示,处于中心的是特征点,其周围分布着采样点。每个圆的半径大小表示对应采样点高斯内核标准差的大小。为了减小噪音对描述符的影响,每个采样点的像素值由对应的高斯内核对其所在感受野进行平滑处理得到。
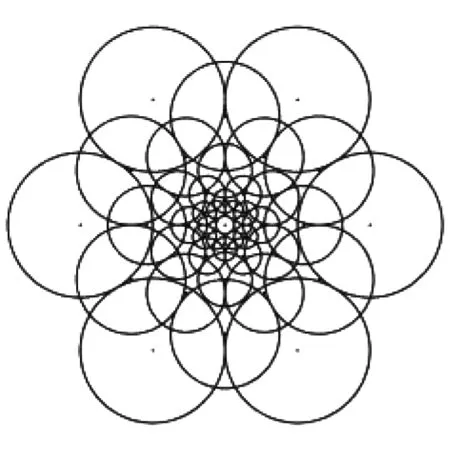
图1 FREAK算法采样模型Fig.1 Sampling model of FREAK algorithm
从图1可以看出,采样点使用不同的高斯内核造成感受野之间存在重叠,这些重叠使得FREAK描述符能捕获更多的信息,从而获得更好的性能。假设在感受野A、B和C中测得的像素强度大小关系如式(1)所示:
IA>IB,IB>IC,IA>IC
(1)
如果感受野没有重叠,那么式(1)中的IA>IC没有为描述符添加任何有用信息。然而,如果感受野存在重叠,则部分新的有用信息能被添加到描述符中。正是因为感受野间存在重叠,FREAK算法用较少的采样点就可对特征点进行充分描述。
1.2 由粗到精的描述符
FREAK描述符通过二值化采样点对之间的像素值差分形成,如式(2)所示:
(2)
其中,F是生成的二进制描述符,Pa表示第a个采样点对,N表示描述符的维度,T(Pa)由式(3)求得:
(3)

为选择更具代表性的点对,FREAK算法利用机器学习算法选择512个高区分度的点对,将其按区分度从高到低分为4组,每组128个,如图2所示。

图2 由粗到精的描述符示意图Fig.2 Schematic diagram of descriptors from coarse to fine
从图2可以看出,第1组点对主要连接外围感受野,最后一组点对主要连接中心区域的感受野,这符合眼球观测物体的行为,人类观测物体时首先用眼球外围的视觉感知细胞去大致确定目标的位置,然后用视网膜中心区域的视觉感知细胞进行确认。FREAK算法根据这种由粗到精的描述符结构提出一种扫视搜索匹配策略。匹配时首先比较前128个点对,即代表粗信息的部分,如果距离小于设定的阈值,则继续比较后续点对,如果距离大于阈值,则停止比较。这种匹配策略加速了匹配过程。
1.3 描述符方向
FREAK算法描述符的方向通过计算局部梯度平均值获得,如式(4)所示:
(4)

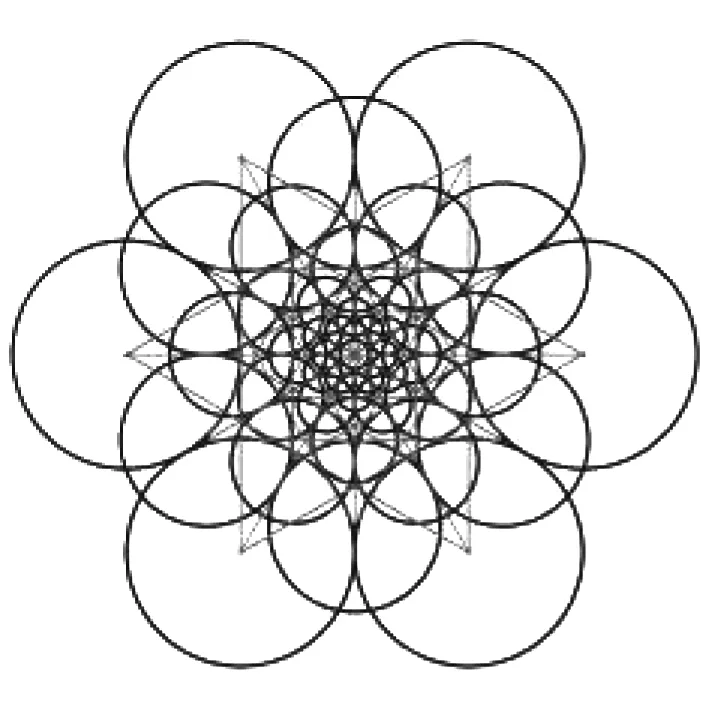
图3 FREAK算法方向点对选取示意图Fig.3 Schematic diagram of the selection of direction point pairs of FREAK algorithm
2 改进FREAK的描述符
2.1 简化的采样模型
FREAK算法区分度最高的第1组点对就可正确区分90%以上的特征[5],这在一方面说明FREAK算法选取的前128个点对具有很高的区分度,另一方面也说明后3组点对的作用相对较弱。本文算法的思路是抛弃区分度不是很高的点对以提高算法的实时性,另外设计一种具有旋转不变性的LBP算法替代这些点对来生成区分度更高的描述符。为了简化计算,根据文献[9]算法的思路将FREAK算法视网膜模型由8 层43个采样点简化为5层25个采样点,简化后的采样模型如图4所示。

图4 简化采样模型示意图Fig.4 Schematic diagram of simplified sampling model
本文利用PascalVOC 2012[12]数据库对简化后的采样模型挑选点对,此数据库包含11 530个图像,从中提取大约200万个特征点,这个规模是FREAK算法训练点对时特征点数量的50倍,大量的训练样本保证了训练结果的鲁棒性。本文参考FREAK[5]和文献[13]设计一种贪婪搜索算法,该算法并非寻找高区分度和高非相关性点对集合的最优解,而是尽可能快地选择一个可行解以提高点对选取速度,具体算法步骤如下:

步骤2计算D每列的均值,再算均值与0.5差的绝对值。将D矩阵各列按此绝对值从小到大排序,根据二项分布均值与方差的关系得到点对按区分度从高到低的排列。建立队列T,将这些点对按序放入队列T。


贪婪搜索算法流程如图5所示。

图5 贪婪搜索算法流程Fig.5 Procedure of greedy search algorithm
通常情形下,在全部300个点对中,算法选出的128个点对能正确区分95%以上的特征点,选出的64个点对能正确区分80%以上的特征点。根据现代计算机架构,位操作一般一次处理128位[5]。本文提出的旋转不变LBP将对简化采样模型生成196位的描述符。为权衡正确率和运行开销,本文从300个点对中用提出的训练算法选取高区分度和高非相关性的64个点对,如图6所示。

图6 简化点对示意图Fig.6 Schematic diagram of simplified point pairs
根据选定的64个点对可生成64维的点对描述符,虽然此描述符尽可能包含更多的信息,但是对比FREAK描述符,维度从512维降到64维,这必然降低描述符的区分度。因此,本文算法用具有旋转不变性的LBP 对感受野进行编码,从而增加描述符的区分度。
2.2 编码感受野信息
根据式(3),FREAK描述符中的每一位都由一对采样点的像素值差分大小关系决定。FREAK算法的这种编码方式仅用一个像素值描述一个感受野,没有充分利用采样模式本身的信息对感受野进行充分描述,这在一定程度上限制了FREAK描述符的区分度。
根据纹理特征可以通过中心像素与邻域像素的差分关系进行表示这一原理,文献[14-15]提出了LBP算法。该算法将中心像素看成一个特征点,LBP作为该特征点的局部描述符。选取邻域像素时可以设置不同的数量P和不同的半径R,如图7所示。
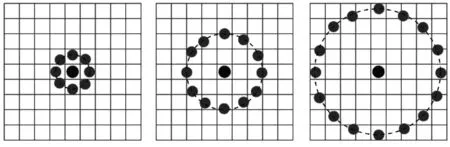
图7 LBP模型图解示意图Fig.7 Schematic diagram of LBP model
LBP的计算如式(5)所示:
(5)
其中,P表示选取邻域像素的数量,R表示选取邻域像素的半径,gp-gc表示第p个邻域像素与中心像素的差分,S(x)由式(6)求得:
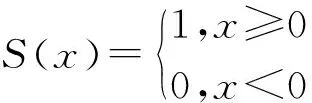
(6)
文献[10]根据这种LBP算法计算差分幅值信息从而增加描述符的区分度。然而原有LBP[14-15]不具有旋转不变性,这是因为当发生旋转时邻域像素取值的先后顺序将发生变化从而破坏旋转不变性。虽然有文献提出了改善LBP旋转不变性的方法[16-18],但这些方法没有利用FREAK采样模式的特有信息而是引入额外的计算,若在FREAK算法中使用这些方法将降低算法的实时性。
FREAK采样模式本身带有方向和尺度信息,本文利用这些信息为每个采样点生成具有旋转不变性的LBP。首先,每个感受野的半径设为已知,则每个采样点LBP的半径可由式(7)求得:
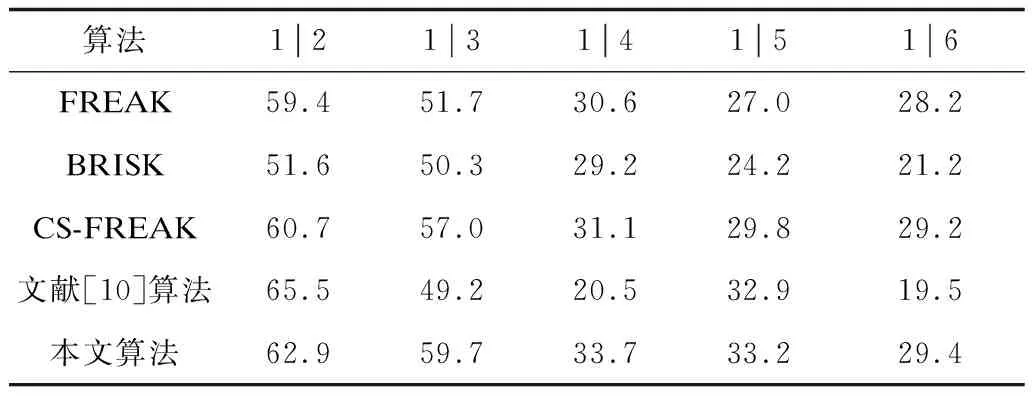
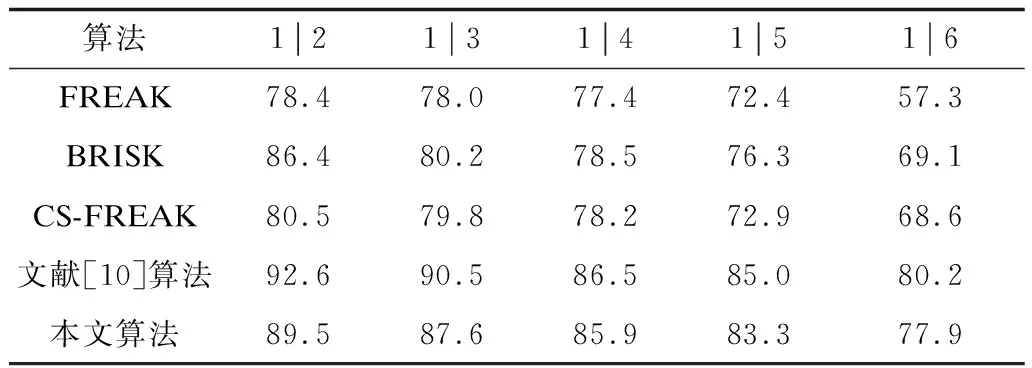
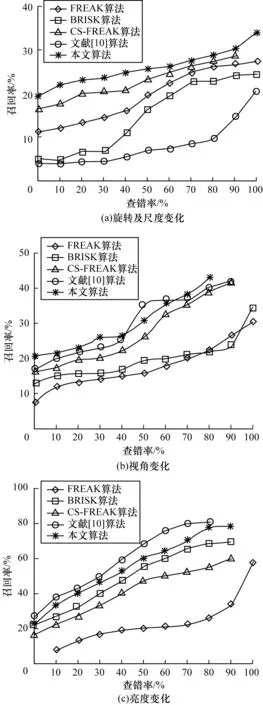
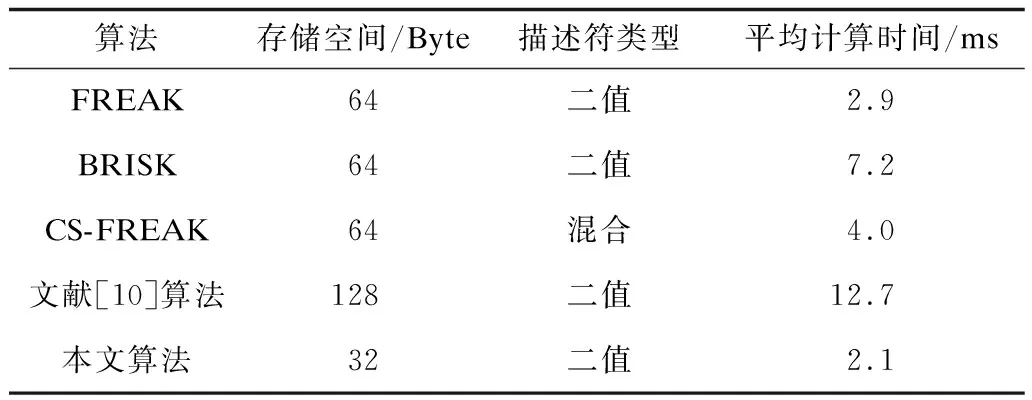
R=k·radius,0 (7) 其中,k是系数,radius是对应感受野的半径。此时,LBP的半径与采样点对应的感受野大小成比例,避免在对大小不同的感受野生成LBP时使用相同的半径。当确定了某采样点的LBP半径R后,以采样点为圆心、R为半径画圆,连接该采样点与特征点画线段。将线段与圆的交点设为该采样点的第0个邻域像素,其他邻域像素按逆时针旋转相应角度得到,如图8所示。 图8 旋转不变LBP模型图解示意图Fig.8 Schematic diagram of rotation-invariant LBP model 从图8可以看出,利用特征点与采样点的相对位置关系选取LBP邻域点,当旋转发生时LBP邻域点的顺序也同时发生旋转,因此生成的LBP具有良好的旋转不变性。 各采样点LBP邻域点的位置可硬编码到采样模式中而无需实时计算。因为算法存储采样模式和计算积分图所需的内存大小是固定的,所以计算描述符时无需动态分配内存。虽然本文算法与FREAK算法记录各自采样模式所需的具体内存大小不同,但2种算法的空间复杂度一致。LBP邻域点取值时的高斯平滑可由积分图近似实现,而积分图在计算采样点取值时就已经建立,所以生成LBP时仅多一个常量级的运算。因此,本文算法的时间复杂度也与FREAK算法一致。 本文描述符的生成过程可分为以下4个步骤: 步骤1对每个感受野生成旋转不变的LBP描述符。 步骤2按感受野从外到里的顺序连接所有LBP描述符,生成本文算法的LBP描述符部分。 步骤3根据2.1节选取的点对计算本文算法的点对描述符部分。 步骤4将连接的LBP描述符放在点对描述符之后,生成本文的描述符。由图6可知,对简化后采样模型选取的64个采样点对主要连接外围感受野,而描述符的LBP部分也按感受野从外到里的顺序连接。因此,本文提出的描述符也可使用扫视搜索策略进行匹配。 计算本文描述符方向的方法与FREAK一致[5],但选取的方向点对有所不同。在简化采样模型后,本文算法选取每层6个采样点两两连接的点对来计算方向,共计60个方向点对,如图9所示。 图9 简化模型的方向点对Fig.9 Direction point pair of simplified model 本文实验所使用的软硬件平台为:Visual Studio 2017,OpenCV 3.4,Intel Core i5-7200U频率2.7 GHz处理器,DDR4 2 400频率8 GB内存。 为验证本文算法的实时性和鲁棒性,实验采用Mikolajczyk数据集[19]和day-night数据集[20]进行测试,这2个数据集中都是单通道图片。Mikolajczyk数据集一共有8个图像序列,分别为bark、boats、bikes、graf、tree、ubc、wall和leuven,每个图像序列为6张图片。其中,bark和boats涉及旋转和尺度变换,graf和wall涉及视角变化,leuven涉及亮度变化,bikes和tree涉及模糊变化,ubc涉及图片压缩变化。day-night数据集共有17个图像序列,每个序列都是同一个摄像头在各种天气环境下拍摄的相同场景。 本文使用召回率及召回率-查错率曲线2种指标来衡量描述符算法,根据召回率分析算法查找出正确匹配的能力,根据召回率-查错率曲线分析算法的鲁棒性。召回率(recall)和查错率(1-precision)的计算可由式(8)求得: (8) 其中,correspondences是指2幅图片间所有的正确匹配数。文献[21]提出2个图片区域之间的重叠错误若小于设定的阈值,则认为是一对正确的匹配。correct matches和false matches分别指描述符算法找到的正确匹配数和错误匹配数。 为了公平起见,本文实验所有描述符都采用STAR特征点,其是CenSurE特征点在OpenCV 3.4中的变种,也是文献[10]算法使用的特征点。Mikolajczyk数据集和day-night数据集都提供精确的单应矩阵,correspondences可根据此单应矩阵直接使用OpenCV 3.4的标准函数获得,选取60%作为重叠错误的阈值。在生成LBP描述符时,根据经验设置邻域点数量P为8,半径R为对应感受野半径的一半,即式(7)中参数k取值为0.5。对Mikolajczyk数据集进行测试,部分测试结果如表1~表3所示,其中,n|m表示将图像序列中的第n张图片与第m张图片进行对比。 表1 boats图像序列召回率Table 1 Recall of boats image sequence % 表2 wall图像序列召回率Table 2 Recall of wall image sequence % 表3 leuven 图像序列召回率 boats序列对应旋转和尺度变化。由表1可知,在旋转角度较小时(1|2图片对),文献[10]算法的召回率最高,本文算法次之。随着旋转角度的增加,文献[10]算法的召回率下降明显,获得了最低的召回率,而此时本文算法仍优于其他算法,这是因为文献[10]算法使用的LBP不具备旋转不变性,而本文算法使用具有旋转不变性的LBP。对于尺度变化(1|5图片对),本文算法与文献[10]算法几乎持平且相对其他算法有较大的优势。 wall序列对应逐渐加大的视角变化。由表2可知,视角变化较小时文献[10]算法略优于本文算法,视角变化较大时本文算法略优于文献[10]算法。而FREAK算法的视角不变性最弱,因此,本文算法对FREAK算法的视角不变性有较大提升。 leuven序列对应逐渐加大的光照亮度变化。由表3可知,文献[10]算法具有较强的光照亮度不变性,本文算法次之,且本文算法对FREAK和CS-FREAK的光照不变性提升较大。 由图10可知,对于旋转及尺度变化,本文算法具有最强的鲁棒性;对于视角变化,本文算法与文献[10]算法性能相近,但在要求低查错率时(小于30%),本文算法优于文献[10]算法;对于简单的光照明暗变化,文献[10]算法具有最强的鲁棒性,而本文算法仅次于文献[10]算法,且对FREAK算法有较大提升。 图10 描述符性能评估Fig.10 Evaluation of descriptor performance 现实世界中不仅存在像leuven序列那样简单的光照明暗变化,更多的是复杂的非线性光照变化,比如day-night数据集提供的图像序列。选取day-night数据集图片序列进行实验,本文算法(下)和原始FREAK算法(上)的正确匹配结果如图11所示。在图11选取的序列中,各种算法的具体匹配结果如表4所示。 图11 本文算法与原始FREAK算法正确匹配结果对比Fig.11 Comparison of correct matching results between this algorithm and original FREAK algorithm 表4 day-night图片序列召回率对比Table 4 Comparison of recall of day-night image sequence 由表4可知,通常情况下,在复杂的光照环境中,本文算法具有最高的召回率,且对比原始FREAK算法,本文算法有较大提升。 除了鲁棒性外,本文还对描述符的实时性进行测试。对各种算法计算1 000个描述符的时间进行统计,采用20次实验的平均结果,如表5所示。 表5 描述符计算时间统计Table 5 Statistics of descriptor calculation time 从表5可以看出,本文算法的实时性最好,这是因为本文算法和FREAK算法在实现时都使用积分图加快计算,且本文算法维度只有FREAK算法的一半。文献[10]算法因其描述符长达1 024位,且生成过程中不仅要计算点对的差分大小,还要计算差分幅值,大幅增加了计算时间。CS-FREAK生成的描述符不是二值描述符,这不仅增加了描述符的生成时间,而且在匹配时也无法使用位运算来加快匹配。 FREAK算法根据人类视网膜设计采样模型,该采样模型优于BRISK算法中人为设计的采样模型。因此,FREAK算法相比BRISK算法具有更好的旋转和尺度不变性。但是,FREAK算法对每个感受野仅用一个像素值进行描述,没有充分利用采样模式信息,导致其视角不变性和光照不变性都比较弱。本文以FREAK算法为基础,根据CS-FREAK算法的思想简化FREAK采样模型,利用机器学习算法在尽可能保证区分度的前提下减少点对数量,从而提高算法的实时性。根据采样模式本身的信息设计一种具有旋转不变性的LBP算法来提高描述符的区分度。实验结果表明,本文算法具有较强的鲁棒性和实时性,且对于光照环境复杂和实时性要求较高的场景具有一定的实际应用价值。本文算法在计算描述符的LBP部分时,需要选取参数k和R,如何针对不同的应用场景来选取最适合的参数将是下一步的研究方向。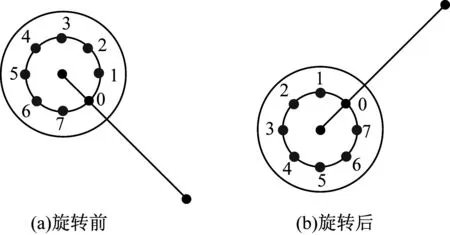
2.3 描述符生成
3 实验结果与分析



4 结束语
