基于攻击防御树的CPS最小防御代价计算方法

钟志成,徐丙凤,顾久根

(南京林业大学 信息科学技术学院,南京 210037)

0 概述

信息物理融合系统(Cyber Physical System,CPS)是一种利用现代传感器技术、计算技术和网络技术实现3C(Computation,Communication,Control)融合,将物理世界和网络世界有效联结的复杂系统,是推动工业4.0发展的核心技术[1]。近年来,CPS被广泛应用于电力、医疗、交通运输、供水(天然气)等工业控制系统,是工业界和学术界的研究热点[2]。由于CPS各个部件之间的通信主要依靠网络,因此其易受网络攻击影响,而CPS物理部件和网络部件之间存在高度耦合性,网络攻击很容易引起物理部件的故障,从而导致严重后果[3]。随着CPS系统不断发展,其面临的攻击手段也在不断更新,攻击方式的多样性和隐蔽性给系统造成了极大的安全威胁[4]。为防止各种网络攻击对CPS造成灾难性后果,对CPS中的一些节点增加防御措施十分必要。但是由于CPS的复杂性很高,针对其中所有节点都增加有效的防御措施比较困难,防御代价较高,因此找到一种既能降低防御代价又能有效防御攻击的方法具有重要意义。

利用攻击树(Attack Tree,ATree)[5]、攻击防御树(Attack Defense Tree,ADTree)[6]、攻击对策树(Attack Countermeasure Tree,ACT)[7]等图形化模型可以对CPS进行风险建模。图形化模型可以直观地体现CPS中攻击者和防御者的行为,为CPS防御策略的分析工作提供便利。文献[8]提出为ADTree中的节点添加攻击事件的攻击收益(Return of Attack,ROA)和防御措施的防御收益(Return of Investment,ROI)两个经济指标,以此评估ADTree的有效性并指导最佳防御策略的选择。文献[9]提出一种ACT和ACT在不同约束下的最优防御措施计算方法,利用约束矩阵和贪心算法计算覆盖攻击节点最多的防御节点的集合。文献[10]利用ADTree建立SCADA(Supervisory Control and Data Acquisition)系统[11]的攻防博弈模型,通过求解该博弈模型的纳什均衡,得到攻防双方的策略选择概率分布结果,从而确定攻防双方为实现自身收益最大化而选择的最优策略。文献[12]利用ATree对智能电网进行风险建模,并基于布尔可满足性问题提出一种最小数目原子节点防御措施计算方法。

当前的研究工作主要以防御措施的数量为标准,在此基础上结合其他经济参数来评估防御策略的优劣,然而防御措施的数量并不能决定系统整体防御代价,选择最小数目的防御措施未必能达到降低防御成本的目的。为此,本文针对CPS的安全防护成本问题,提出一种CPS最小防御代价的计算方法,并设计相应的计算软件,以提高防御措施的有效性。

1 相关工作

目前对CPS做安全风险评估的定性分析方法,典型的有攻击树、攻击防御树、故障树、攻击图等。攻击树[5]是一种系统化的攻击场景建模方法,文献[13]对其做了正式的定义。攻击树按从上至下的顺序逐层建模攻击场景,将攻击目标逐层分解成原子攻击,可以对攻击场景做定性和定量分析,被广泛应用于系统安全性评估。但是攻击树仅能描述攻击场景,无法体现攻击者和防御者之间的交互行为。为此,文献[6]提出了攻击防御树的概念。攻击防御树在攻击树的基础上增加了防御节点,可以建模攻击防御场景从而对系统进行安全评估。

文献[14-19]利用攻击防御树对CPS进行定量风险评估。文献[14]针对SCADA系统提出一种基于层次分析法和攻击防御树模型的SCADA系统脆弱性评估方法。文献[15]利用ADTree对CPS进行风险评估,并提出两个经济指标来评估攻击防御树的有效性。文献[16]基于攻击防御树提出一种针对APT攻击的风险评估理论模型。文献[17]通过网络攻防行为树来描述网络攻防场景并利用该模型评估防御措施的效果。文献[18]利用带时序逻辑的拓展攻击防御树模型,构建一种基于博弈论方法的攻击防御场景分析框架。文献[19]针对高级持续性威胁,建立一种攻击防御树量化模型,同时分析攻击行为对防御措施的影响。然而,目前的攻击防御树定量分析方法较少考虑对最小防御代价的计算,本文将对此进行研究。

2 最小防御防御代价计算方法

2.1 计算流程

为求解CPS的最小防御代价,首先要用ADTree建模CPS中的攻击事件和防御事件。建模完成后,需要对ADTree进行转换以提高算法效率,然后计算转换得到的ADTree的径集,最后计算径集对应的防御代价并找到最小防御代价。最小防御防御代价计算流程如图1所示。

图1 最小防御代价计算流程

2.2 原子攻击防御树

如果基于传统的ADTree来求解最小防御代价,则需要递归查询ADTree的子树,效率较低。为此,本文提出原子攻击防御树(Atom Attack Defense Tree,A2DTree)的概念。A2DTree是一种特殊类型的ADTree,其对一般的ADTree做了如下限制:1)根节点的类型是攻击节点;2)只有原子节点才有相应的防御节点,其他节点没有防御节点。由于A2DTree的结构比较特殊,因此要求解A2DTree的最小防御代价,只需要求解A2DTree的径集并代入防御代价进行计算,即可求出最小防御代价。A2DTree示例如图2所示。

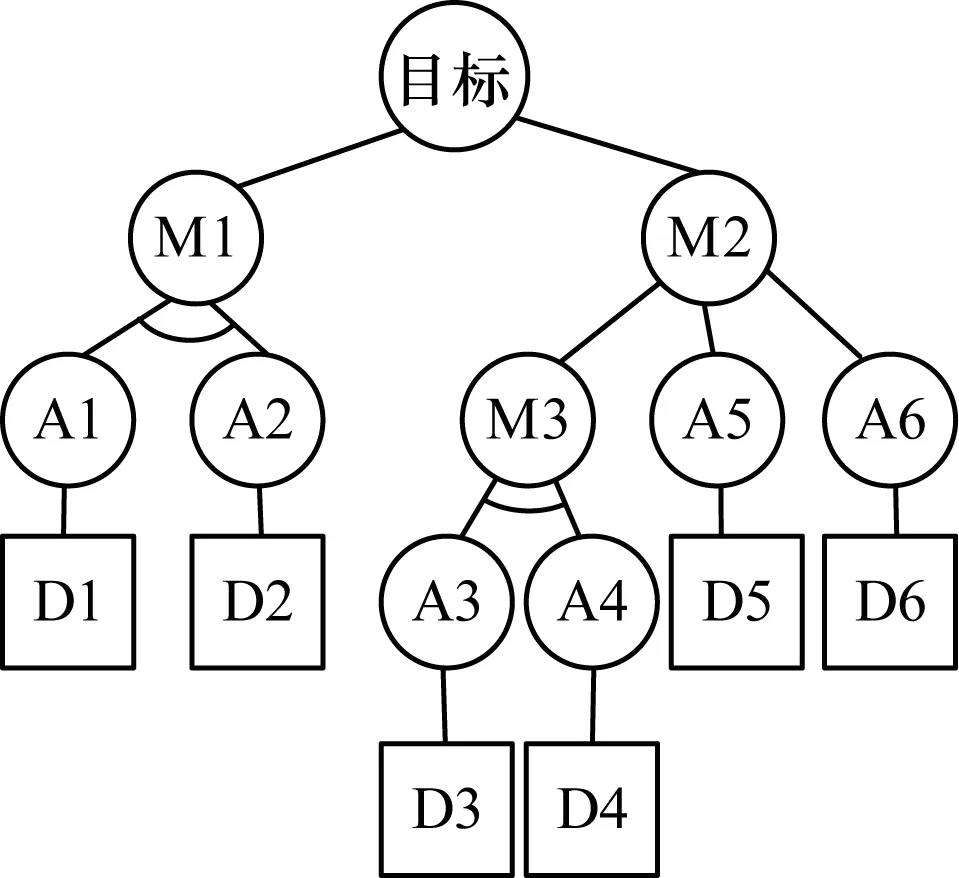
图2 原子攻击防御树示例Fig.2 Example of atom attack defense tree

原子攻击防御树的形式化描述如下:

A2DTree=,V=Vat∪Vdf

其中:Vat表示所有攻击节点的集合;Vdf表示所有防御节点的集合;e={vs,vd}∈E,表示一条从节点vs到vd的边;Q={AND,OR,SAND},表示攻击防御树中逻辑门的集合;vr∈Vat,表示根节点;Vl表示原子攻击节点的集合,Vdf和Vl存在一一映射关系。

割集和径集提供了关于系统脆弱性的重要信息,下面给出原子攻击防御树割集和径集的定义。

定义1原子攻击防御树的割集是导致顶部攻击事件发生的基本攻击事件的集合。

∃Vc,∀vc∈Vc,有vc∈Vl,若集合Vc中的攻击事件全部成功,顶层攻击会成功,则Vc是A2DTree的一个割集,Vl是原子攻击节点的集合。

定义2原子攻击防御树的径集是保证顶部攻击事件不发生的基本攻击事件的集合。

∃Vp,∀vp∈Vp,有vp∈Vl,若集合Vp中的攻击事件全部失败,顶层攻击会失败,则Vp是A2DTree的一个径集,Vl是原子攻击节点的集合。

2.3 算法描述

2.3.1 攻击防御树到原子攻击防御树的转换算法

针对中间攻击节点也有防御节点的常用ADTree,利用A2DTree的特征求解其最小防御代价,提出一种将一般ADTree转化为与A2DTree结构一致的等价树的算法。利用转化后的ADTree来求解最小防御代价,可以提高ADTree最小防御代价计算算法的性能。

ADTree转化为A2DTree的形式,需要将所有存在防御子节点的中间攻击节点下移,使中间攻击节点成为叶子节点。下移过程分为以下5个步骤:

1)构造2个中间替补节点T1、T2。

2)将需要下移的中间节点N1添加到T1的子节点集合中。

3)将原N1的子节点添加到T2的子节点集合中,原N1子节点之间的逻辑关系不变。

4)将T2节点添加到T1的子节点集合中,T1子节点之间的逻辑关系为AND。

5)将T1节点添加到原N1父节点的子节点集合中。

从ADTree的根节点开始递归遍历,对有防御子节点的中间节点执行上述下移过程,可得到最小防御代价与原ADTree相等的A2DTree。ADTree转化为A2DTree的示例如图3所示。

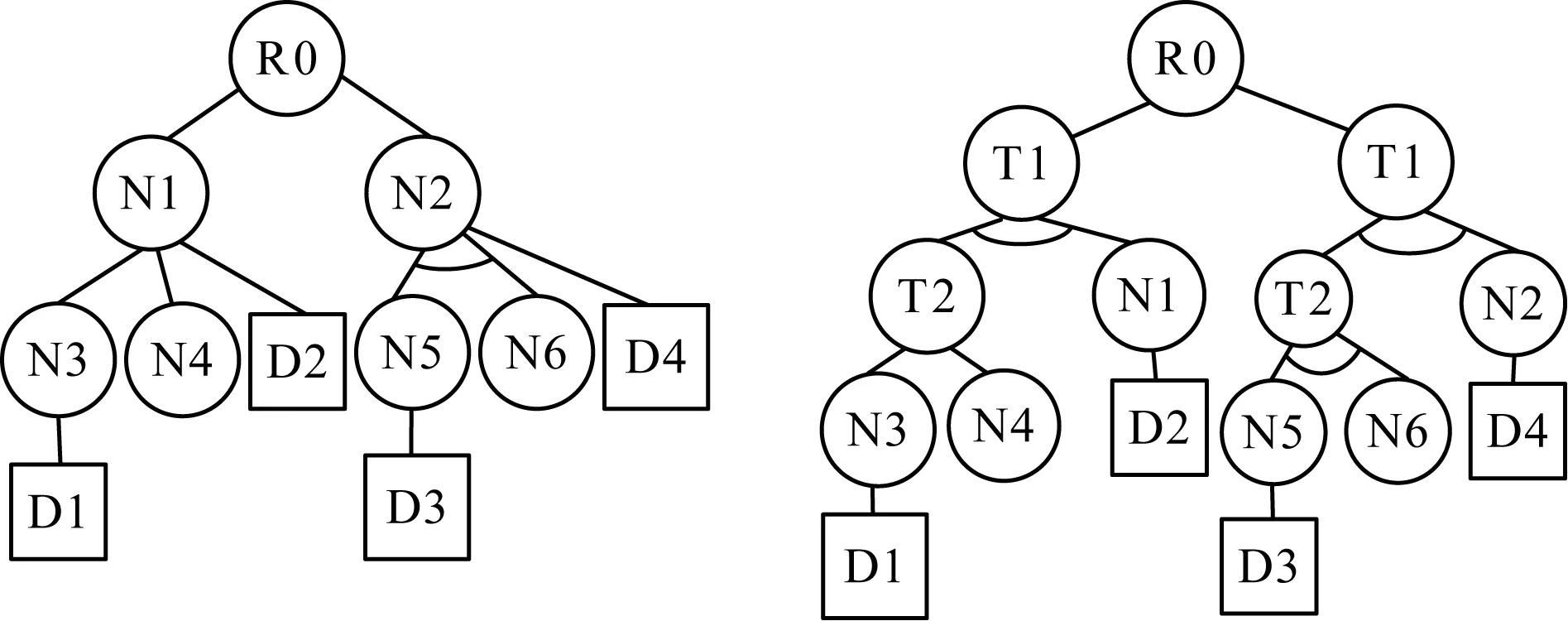
图3 攻击防御树转化为原子攻击防御树的示例Fig.3 Example of attack defense tree being transformed into atom attack defense tree

可以证明ADTree中任意子树的最小防御代价和经过转换得到的新子树的最小防御代价相等。假设ADT1是ADTree中某一棵以N1为根节点的子树,N1为中间攻击节点并且有防御节点D1。ADT1能防御成功且防御代价可能最小的方案有2种:1)采用D1防御节点;2)不采用D1防御节点,采用ADT1中其他所有能防御成功的防御节点组合中防御代价最小的组合。2种方案对应的最小防御代价分别为C1、C2,ADT1的最小防御代价MinCost1为C1、C2中的较小值。ADT1经过转换后得到ADT2,N1移动成为叶子节点。假设T1是ADT2的根节点,T2是N1原来的子节点的新父节点。因为N1和T2之间的逻辑关系为AND且T1、T2没有防御子节点,所以ADT2防御成功且防御代价可能最小的方案有2种:1)采用D1防御措施;2)采用使T2防御成功的防御节点组合中防御代价最小的组合。2种方案对应的最小防御代价分别为C3、C4,ADT2的最小防御代价MinCost2为C3、C4中的较小值。因为C1=C2,C3=C4,所以MinCost1和MinCost2相等,即ADT1的最小防御代价和ADT2的最小防御代价是一致的。推广以上结论,可以证明ADTree的最小防御代价和A2DTree的最小防御代价相等。

假设待求解的ADTree共有A个攻击节点和D个防御节点。攻击防御树的转换过程,实际上是遍历整个ADTree并把有防御节点的中间攻击节点下移的过程,因此,转换算法具有线性时间复杂度O(A+D)。

算法1攻击防御树转换为原子攻击防御树

输入攻击防御树ADTree

输出原子攻击防御树A2DTree

1.procedure ConverseToA2DTree(节点root)

2.Children:={root的子节点集合};

3.NewChildren={};

4.i:=1;

5.repeat

6.child:=Children中第i个节点;

7.if child是中间攻击节点且有防御子节点

8.then

9.T1:=新的攻击节点;

10.T1的子节点关系:=child的子节点关系;

11.T1的子节点:=child的子节点;

12.T2:=新的攻击节点;

13.T2的子节点关系:=AND;

14.将child添加到T2的子节点集合中;

15.将T1添加到T2的子节点集合中;

16.call conversToA2DTree(T1);

17.将T2添加到Newchildren中;

18.else

19.call ConversToA2DTree(child);

20.将child添加到Newchildren中;

21.end if

22.i:=i+1;

23.until i=Children的子节点个数+1;

24.root的子节点集合:=NewChildren;

25.end procedure

26.NewRoot:=新的根节点;

27.将ADTree的根节点添加到NewRoot的子节点集合中;

28.call ConverseToA2DTree(NewRoot);

2.3.2 最小防御代价求解算法

将ADTree转化为A2DTree后,利用成功树法求A2DTree的径集。求出A2DTree的对偶树,将原A2DTree中的AND换成OR,OR换成AND,对偶树的割集就是原A2DTree的径集。本文采用代数法求攻击防御树的割集,具体步骤如下:

1)将A2DTree的攻击节点看作布尔变量,从根节点开始逐层向下递归,计算出用原子攻击节点表示根节点的布尔表达式。

2)展开布尔表达式,得到一个析取范式(DNF)。

3)提取该DNF中的每一个简单合取式,合取式中所有文字对应的攻击节点构成的集合即A2DTree一个割集。

求出A2DTree的所有径集后,计算各个径集中所有原子攻击对应防御代价之和,所有防御代价中的最小值即为最小防御代价。

假设待求解的ADTree共有A个攻击节点和D个防御节点,其中有防御节点的中间攻击节点有A1个。ADTree转换得到的A2DTree有(A+2A1)个攻击节点和D个防御节点。算法需要遍历整个A2DTree求得由原子攻击节点组成的布尔表达式来计算最小防御代价,因此,其时间复杂度为O(A+2A1+D)。

算法2计算攻击防御树最小防御代价

输入原子攻击防御树A2DTree

输出A2DTree的最小防御代价和需要防御的攻击节点集合

1.BooleanExpression:=A2DTree的逻辑表达式;

2.PathSets:={BooleanExpression中的所有简单合取式,即A2DTree所有径集的集合};

3.MinCost:=+∞;

4.PathSet:={};

5.j:=1;

6.repeat

7.pathset:=PathSets中的第j个径集;

8.cur_cost:=cutset对应的防御代价;

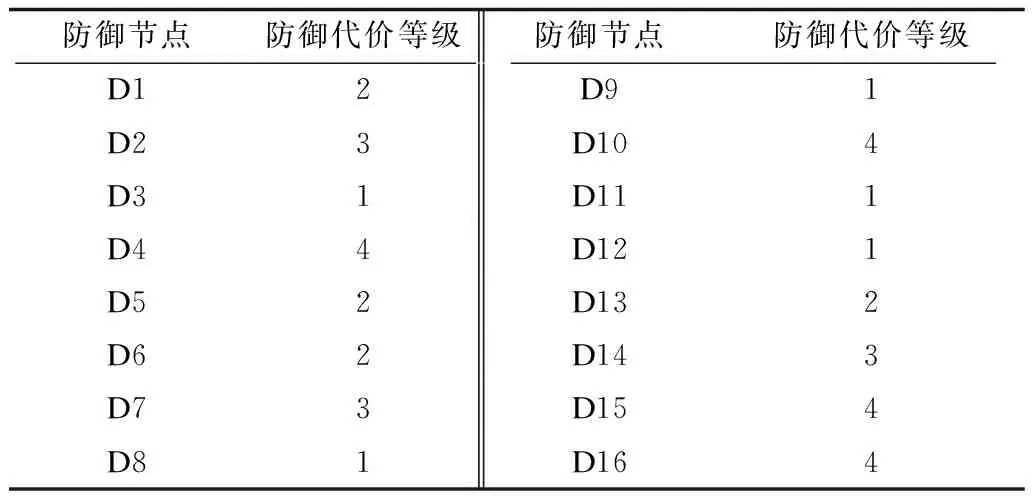
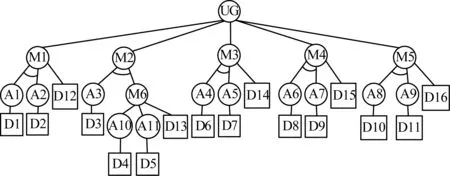
9.if cur_cost

10.then

11.MinCost:=cur_cost;

12.PathSet:=pathset;

13.end if

14.j:=j+1;

15.until j=PathSets中子集合的个数+1;

3 软件实现与实验分析

3.1 软件实现

基于攻击防御树建模方法,本文在Eclipse平台上利用Java语言实现了最小防御代价计算软件(获取地址为https://github.com/zzc1/ADTree_Min_DefCost/releases/tag/1.0),其用户界面如图4所示。具体实现功能如下:

图4 最小防御代价计算软件用户界面Fig.4 User interfaces of the minimum defense cost calculation software

1)导入攻击防御树建模工具生成的XML文件,生成相应的攻击防御树模型。

2)为防御节点赋予防御代价属性值。

3)将攻击防御树转换成为原子攻击防御树。

4)计算出原子攻击防御树的所有径集和相应的防御代价,并排序输出。

3.2 实例分析

下面以文献[20]中电力系统的SCADA系统为例,对本文提出的方法进行验证。SCADA系统由控制中心网络、控制中心和变电站之间的通信网络、变电站自动化系统等网络组件构成,攻击者利用网络组件的漏洞可以对SCADA进行攻击,获得非法的操作权限,从而给电力系统造成安全隐患和经济损失[20]。在本实例中,攻击者通过网络攻击向控制保护继电器发出跳闸命令,导致断路器无故障跳闸,从而造成停电。通过本文方法给文献[20]中的攻击树添加防御节点,所得到的攻击防御树如图5所示,其中各节点的具体含义如表1所示。

图5 断路器无故障跳闸攻击防御树

表1 攻击防御树各节点的含义

通过对防御措施的实现难度、需要的时间和资金等因素进行综合评估,评估人员根据实际情况对防御代价等级进行评级,得到各防御节点的防御代价等级,等级如表2所示。

表2 各防御节点防御代价等级Table 2 Defense cost levels of defense nodes

利用攻击防御树建模软件对攻击防御树进行建模,并将模型输出为XML文件导入攻击防御树最小防御代价计算软件。文件导入结果如图6所示。

图6 XML文件导入结果Fig.6 Result of XML file import

选择“添加防御代价属性”为防御节点添加防御代价值,防御代价值是一个非负实数,使用具体值还是防御代价等级用户可自行选择。属性赋值结果如图7所示。

图7 属性赋值结果Fig.7 Result of attribute assignment

属性赋值完成后,选择“计算防御代价”计算最小防御代价,所有的计算结果会按防御代价的大小升序显示在弹出的文本框中。部分计算结果如图8所示。

图8 部分计算结果Fig.8 Partial calculation results

由最小防御代价计算工具输出的结果可知,有2个节点集合对应的防御代价最小。根据该结果,可以对集合中相应的攻击节点加强防御,降低防御成本。

3.3 性能比较

为进行相关工作的对比,本文采用文献[21]中的软件ADTool对ADTree进行最小防御代价计算,ADTool采用的是自顶向下递归算法(UTDRE_ALGO),该算法需要计算原树的所有包含根节点的子树的径集。上文提出的先将攻击防御树进行转换的算法(CONV_ALGO)则需要计算转换后的攻击防御树的径集。为判断两种算法的优劣程度,分别用两种算法求解5个ADTree模型的最小防御代价,并统计算法的时间和空间消耗。所有的实验均是在一台双核四线程,CPU频率为2.5 GHz、内存为8 GB的计算机上完成的,实验结果如表3所示。

表3 两种算法的时间和空间消耗

由表3可知,CONV_ALGO的时间和空间消耗都优于UTDRE_ALGO。UTDRE_ALGO的时间复杂度和攻击防御树的包含根节点的子树个数有关,CONV_ALGO的时间复杂度和攻击防御树的节点个数有关。当攻击防御树的规模比较大时,子树的个数会比较多。例如实验中的攻击防御树E,经过粗略计算,树E中包含根节点的子树个数约有50 000个,即UTDRE_ALGO需要计算约50 000个ADTree的径集,而CONV_ALGO只需计算转换后的A2DTree的径集,从而减少了计算径集的时间,提高了效率。

4 结束语

本文对CPS安全防御代价评估问题进行研究,通过建模攻击防御树和求解径集,设计一种适用于CPS 的防御代价计算方法。基于攻击防御树给出原子攻击防御树的概念,将攻击防御树转换成原子攻击防御树,在此基础上求解原子攻击防御树的径集并计算相应的防御代价。实例验证结果表明,该方法较自顶向下直接求解的算法效率更高。后续将进一步改进攻击防御树的结构,对带有时序逻辑的攻击防御树进行最小防御代价求解,同时优化攻击防御树径集的求解方法,减少中间过程,从而提高算法效率。