MATLAB软件在生物统计理论教学中的应用——以抽样分布为例

应智霞， 张 欢， 葛 刚， 邹志文

(南昌大学 生命科学学院， 南昌 330031)

生物统计学是数理统计的原理在生物科学中的应用，微生物学、植物学、动物学等各领域研究中都离不开生物统计，如生物学实验设计、取样、数据处理与分析，资料的归纳与总结。生物统计学不仅仅是诸多高校医学、生命科学、农业科学等领域的必修专业基础课，也广泛应用于科学研究和生产实践。通过对这门课程的系统学习，培养学生发现与分析问题的能力，满足新时代对创新型和应用型人才的需求[1-3]。然而，由于其具有较强的理论性和抽象性，学生反映这门课程难懂、难学以及枯燥单调，导致这门课程的教学效果不是很好[4-6]。

要提高生物统计学的教学效果以及培养学生对统计知识的综合应用能力，必须要掌握生物统计的原理与方法。生物统计学最基本的问题是研究总体与样本间的关系，其可以通过两方面研究：1)由已知的总体，研究样本统计量的分布规律，即由总体到样本的研究过程；2)以样本统计量的抽样分布为基础，由样本去推断未知的总体。抽样分布在概率论和推断统计中具有承上启下的作用，但抽样分布抽象、复杂，很多初学者难以理解。如何正确理解抽样分布是后续统计推断的基础，也是对生物统计原理与方法必需掌握的基本内容。如果学生不能正确地认识抽样分布以及其主要统计作用，就会无法准确区分后续的统计推断与假设检验中相关定义(如标准差，标准误差)，进而无法有效掌握统计推断的原理。

抽样分布就是样本统计量的分布。如果在大量样本的抽样实验中，能通过实验模拟的方法，得出分布的结论，这样会使学生更加直观地理解这部分内容。计算技术的发展为理论分布及检验提供了一种更直观的表达方法，即用计算机模拟的方法使理论问题实验化，抽象问题具体化，并对理论进行模拟验证[7-10]。MATLAB 是美国MathWorks公司面对科学计算、可视化以及交互式程序设计的高科技计算环境。它具有完备的图形处理功能、计算运算能力和编程的可视化，是生物统计这门课辅助教学的一个有力工具。针对那些内容抽象、学生难以理解、用传统教学方法难以奏效的教学内容开展MATLAB系统辅助教学，可以让学生更直观、更深刻地理解教学知识点。

基于此，本文介绍了如何利用MATLAB软件对3种常见的抽样分布进行描述和验证，让学生更直观、更深刻地理解三大抽样分布的内涵，为教学提供一种更直观的抽样实验方法，改进统计课程的教学。

1 抽样分布的定义

总体(population)是指考察对象的全体。描述总体特征的数值记为参数，是一个不变的常数；样本(sample)是总体中所抽取的一部分个体，样本中个体的数目记为样本容量n。描述样本特征的数值记为统计量，是一个随机变量。从一个已知或者未知的总体中，独立随机地抽取含量为n的样本，所得样本的各种统计量的概率分布，即所谓的抽样分布(sampling distribution)。以样本平均数为例，如果按照相同的样本含量n，相同的抽样方式，反复地进行独立随机抽样，每次都可以得到一个含量为n的样本，计算每个样本的平均数，所有可能样本的平均数所形成的分布，就是样本均值的抽样分布(图1)，其中统计量的抽样分布往往是一种理论分布，因为现实中一般不可能将所有的样本都抽出来。

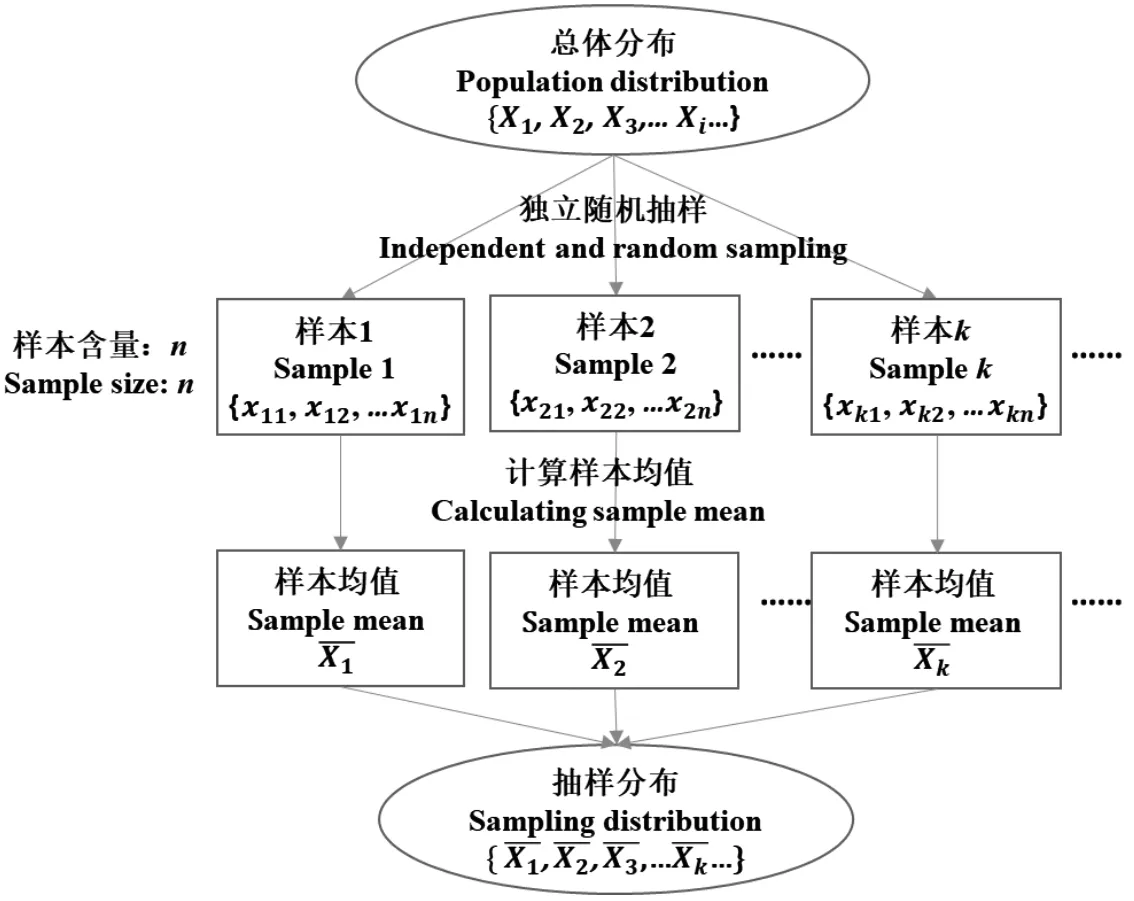
图1 样本均值的抽样分布

2 生物统计学中常见的抽样分布

生物统计学最基本的问题是研究总体与样本间的关系，主要从两方面研究：一是从已知总体研究样本的分布规律；二是从样本推断未知的总体。其中，研究的“样本的分布规律”通常指样本统计量的分布规律，即抽样分布，只有理解和掌握抽样分布，才能有效利用样本对总体做出统计推断。对一个从均值为μ，标准差为σ的正态总体(即X～N(μ,σ2))中抽取的样本统计量的分布主要有如下几种：

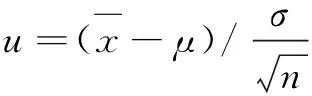
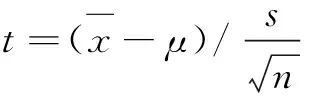
3)标准化的样本方差χ2=(n-1)·s2/σ2服从自由度df=n-1 的χ2分布。

3 基于MATLAB模拟抽样分布的思路

从一个正态总体中抽取样本统计量分布的模拟过程主要包括以下步骤：

1)已知一个总体X～N(μ,σ2)，重复地从这个正态总体中独立随机地抽取容量为n的样本NS个；

2)计算每个样本的平均数(记mi，i=1,2,…,NS)与标准差(记si，i=1,2,…,NS)；

3)计算3种统计量(即ui，ti，χ2i)的值(i=1,2,…,NS)；

4)分别做出3种统计量的频率分布图，当NS很大时，频率分布图近似抽样分布的概率密度分布；

5)并分别将这3个频率分布图和相应的理论分布进行比较，验证从正态分布总体中抽取样本统计量分布的形式。

在MATLAB平台下的具体实施流程见图2，其中涉及的MATLAB函数说明见表1。

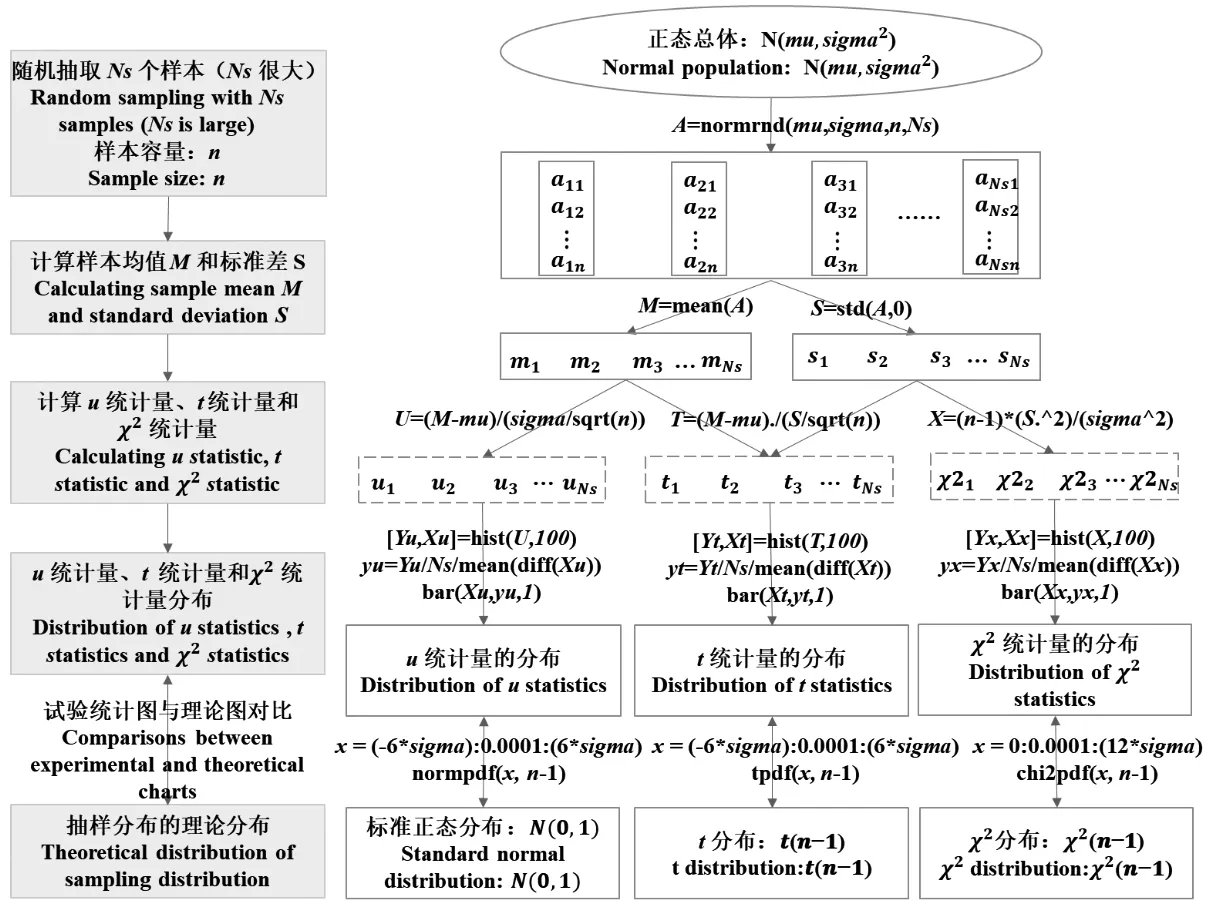
图2 模拟与验证从正态分布总体中抽取样本统计量分布的流程图

4 模拟结果

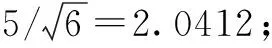
表1 主要相关MATLAB函数介绍

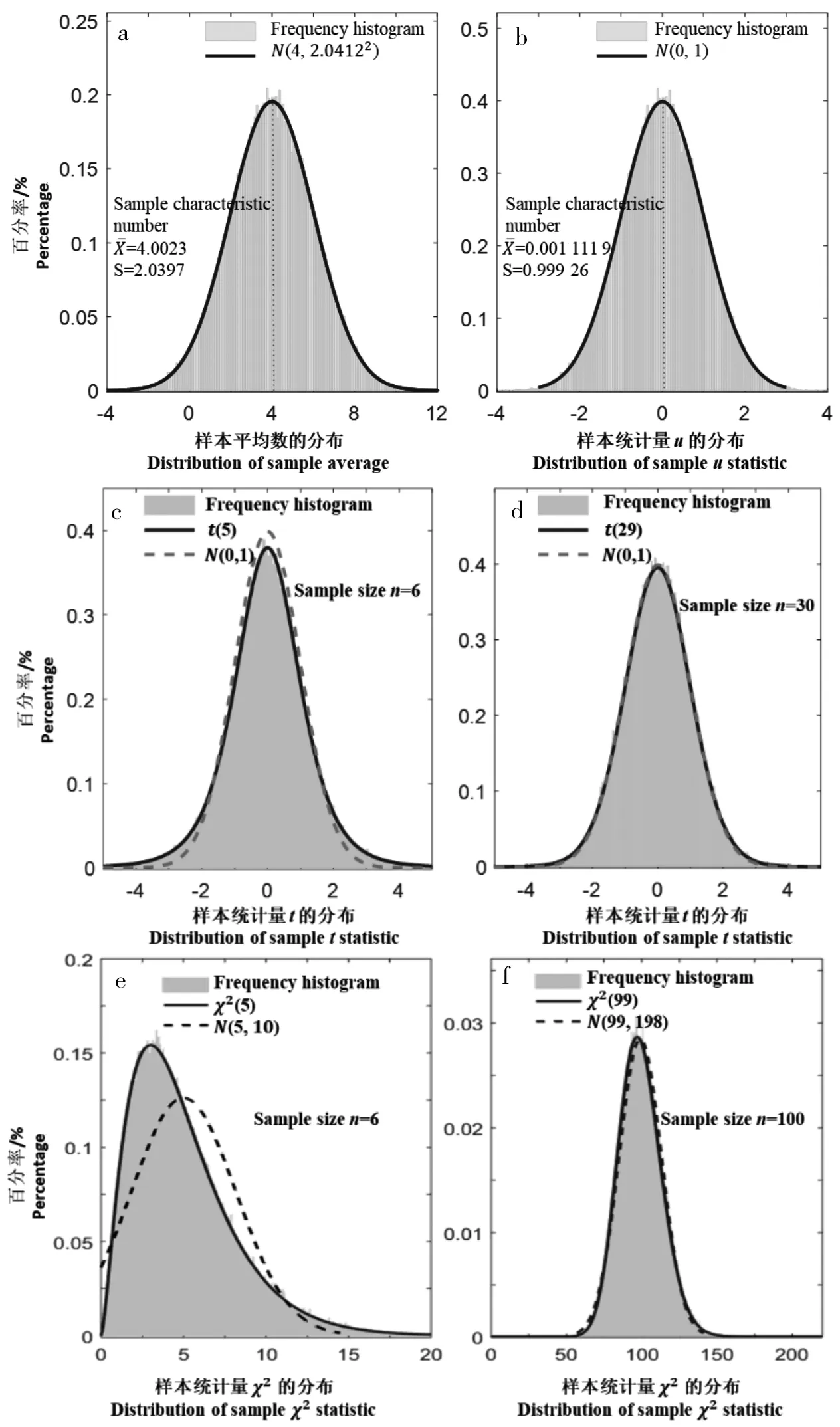
图3 从一个正态总体中的抽样分布模拟验证

此外，对于样本t统计量和样本χ2统计量，还分别模拟了样本容量n=30和100 的情况。对于样本t统计量的模拟实验，可以看出，在自由度比较小的时候，t分布与标准正态分布相差较大，随着自由度变大，t分布在自由度等于29的时候与标准正态分布重合度较高。结果验证了当t分布的自由度增大时，t分布趋于标准正态分布(图3-c、d)，也说明了在样本量大于30的时候，t-检验和u-检验可以相互替换使用；对于样本χ2统计量的模拟实验，可以看出，在df=5 的时候，χ2分布与正态分布N(5,10) 偏离较大，在df=99的时候，x2分布与正态分布N(99,198) 重合度较高，验证了当χ2分布的自由度增大时，χ2分布趋于正态分布，其中正态分布的均值为χ2分布的自由度，方差为自由度的2倍(图3-e、f)。

5 总结

在生物统计课程教学中，关于抽样分布这部分内容的讲解是一件棘手的事情，学生难以理解抽样分布的内涵以及对其在统计推断中的应用。抽样分布其实就是样本统计量的分布，利用实验模拟的方法得出大量样本统计量的分布，学生就能更加直观地去理解抽样分布。本文通过MATLAB软件编写程序进行模拟抽样，获得了3种常见的抽样分布的样本分布，试验统计结果与理论结果非常一致，表明本实验方法能有效地模拟抽样分布，为抽样分布的描述和验证提供一种更直观的抽样实验方法。

模拟试验的模拟结果直观形象地呈现了几种常见的抽样分布，使抽象的统计理论问题具体化。MATLAB软件为生物统计理论进行模拟验证提供辅助手段，可以增强学生对所学知识的理解。通过MATLAB软件，通过调节总体参数、样本容量等参数，查看不同参数下几种常见的抽样分布及参数变化情况，从而使学生更加直观地理解总体与样本之间的关系，进而快速掌握样本抽样分布。另外，通过MATLAB辅助教学可以增加生物统计学学习的趣味性，调动学生学习积极性，将显著提升教学效果，培养出具备良好统计基础才能的创新性人才。