熔盐堆功率自抗扰控制方法研究
2020-08-19罗志鹏王培琳周世梁赵鹏飞姜泽雨
刘 枭 罗志鹏 王培琳 周世梁,2 赵鹏飞 姜泽雨
1(华北电力大学 北京 102206)
2(非能动核安全技术北京重点实验室 北京 102206)
熔盐堆是以流动的熔盐作为燃料的新型反应堆堆型,具有良好的中子经济性、固有安全性、可在线后处理、可持续发展、防核扩散等优点,被第四代国际核能论坛确定为6种第四代先进核能系统的候选堆型之一。熔盐堆(Molten Salt Reactor,MSR)最早是由美国橡树岭国家实验室(Oak Ridge National Laboratory,ORNL)启动。1965年,ORNL 建造的MSRE(Molten-salt Reactor Experiment)达到临界,并成功运行10 000多个小时论证了熔盐堆的可行性[1]。研究一个堆型,特别是一个新型堆型,一定离不开对它的功率控制研究。因此,为保证其可行性与安全性,需要设计一个简单而高性能的控制系统来控制熔盐堆的功率。
控制系统的首要目的是使系统稳定运行,不受非期望因素的影响,或者受到影响后能及时加以纠正,使系统保持在期望的状态。目前普遍应用的控制技术PID(Proportion Integration Differentiation),是对比例(P)、积分(I)、微分(D)三个参数进行调整,就可以使被控系统获得较为满意的控制性能。但是PID是被动地通过误差反馈来消除误差,存在滞后性等缺陷[2]。因此本文采用主动进行扰动抑制的思想方法,即构建一个观测器来估计外部扰动/内部不确定性(或两者),然后相应地加以补偿,抑制扰动对输出的影响。目前以此思想为基础形成的技术成果主要有,干扰适应控制(Disturbance Accommodation Control,DAC)、基于扰动观测器(Disturbance Observer,DOB)等。但是这些控制方法大多设计复杂,参数整定方面难度大且不易在工程上实现。因此,本文基于自抗扰控制(Linear Active Disturbance Rejection Control,ADRC)理论[3],设计了一种抗扰性能强、结构简单、参数整定方便的自抗扰控制器。ADRC技术是韩京清教授在经典控制论思想的精华上逐步构建,并于1999年正式提出的。其核心思想是以简单的积分串联型为标准型,把系统动态中不同于标准型的部分(包括系统的不确定性以及扰动)视为总扰动(包括内扰和外扰),以扩张状态观测器为手段,实时地对总扰动进行估计,并加以消除,从而把充满扰动、不确定性和非线性的被控对象还原为标准的积分串联型,使得控制系统的设计从复杂到简单,从抽象到直观。ADRC主要由跟踪-微分器(Tracking Differentiator,TD,用于微分信号获取和过渡过程配置)、扩张状态观测器(Extended State Observer,ESO,用于总扰动的观测)以及非线性状态误差反馈控制率(Nonlinear State Error Feedback,NLSEF,用于控制量生成)组成。因为ADRC的几乎模型无关性,灵活性和易用性,所以本文采用ADRC为基础设计自抗扰控制器。
本文将解决以下问题:1)从熔岩堆非线性模型导出用于控制器设计的相对功率的二阶非线性模型;2)设计出扩张状态观测器;3)设计出自抗扰控制器,观测其输出扰动估计。
1 非线性快堆堆芯模型
堆芯模型由中子动力学、传热模型和反应性反馈模型三个子系统组成,将在以下部分讨论。
1.1 中子动力学方程
非线性、六组缓发中子先驱核点堆动力学方程如式(1)、(2)所示[4]。

式中:N是中子密度;β是总有效缓发中子份额;ci是第i组先驱核浓度;βi是第i组缓发中子的份额;λi是第i组衰变常数;Λ是不变的中子平均寿命;ρ是反应性;τc是燃料流经堆芯内时间;τL是燃料流经堆芯外部的时间。
1.2 热传输方程
基于单通道平均温度假设,在燃料、冷却剂和包壳之间的建立简单传热方程。“一石墨两燃料”(onegraphite two-fuel,1G-2F)带热交换器的反应堆堆芯模型,如图1所示。
以下是每个区域所代表的各自的常微分方程[5]:
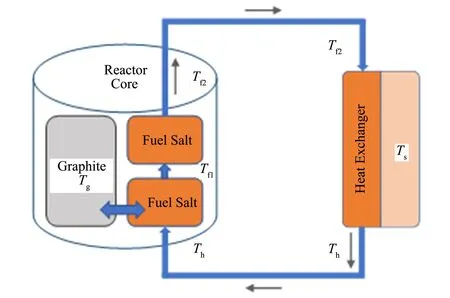
图1“一石墨两燃料”带热交换器的反应堆堆芯模型Fig.1 1G-2F model of the reactor core with the heat exchanger

式中:mf是堆芯燃料盐质量;mg是堆芯石墨质量;Tf1是平均燃料温度(节点1);Tf2是平均燃料温度(节点2);Th是换热器燃料盐平均温度;Tg是石墨平均温度;Ts是散热器温度;γf是燃料内部产生的热量的部分;γg是石墨内部产生的热量的部分;cp,g是石墨的比热容;cp.f是燃料比热容;kf,g是燃料对石墨传热系数;kh,s是换热器传热系数;P是反应堆功率;mf是堆芯燃料盐进口速率。
石墨和燃料熔盐间直接发生热交换,对于上述两燃料节点的模型,燃料质量和与石墨的接触面积平均分配给两个燃料节点,因此方程(3)和(4)中燃料对石墨传热系数取kf,g/2。
1.3 反应性反馈方程
反应性是堆芯动态特征最重要的参数之一,反应性反馈系统相对简单,易于实现,因为它只包含一个方程[5]:
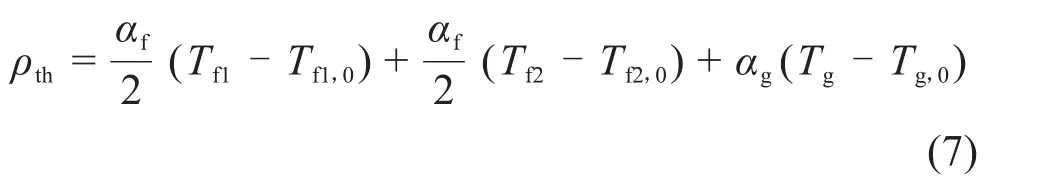
式中:ρth是固有的热反馈反应;αf是燃料反应性温度系数;αg是石墨反应性温度系数;Tg是石墨平均温度。
由于熔盐堆具有液态燃料的特点,反应性温度系数αf和αg都包括了密度和温度两方面效应[6]。
1.4 模型参数
表1为石墨慢化熔盐堆参考数据。
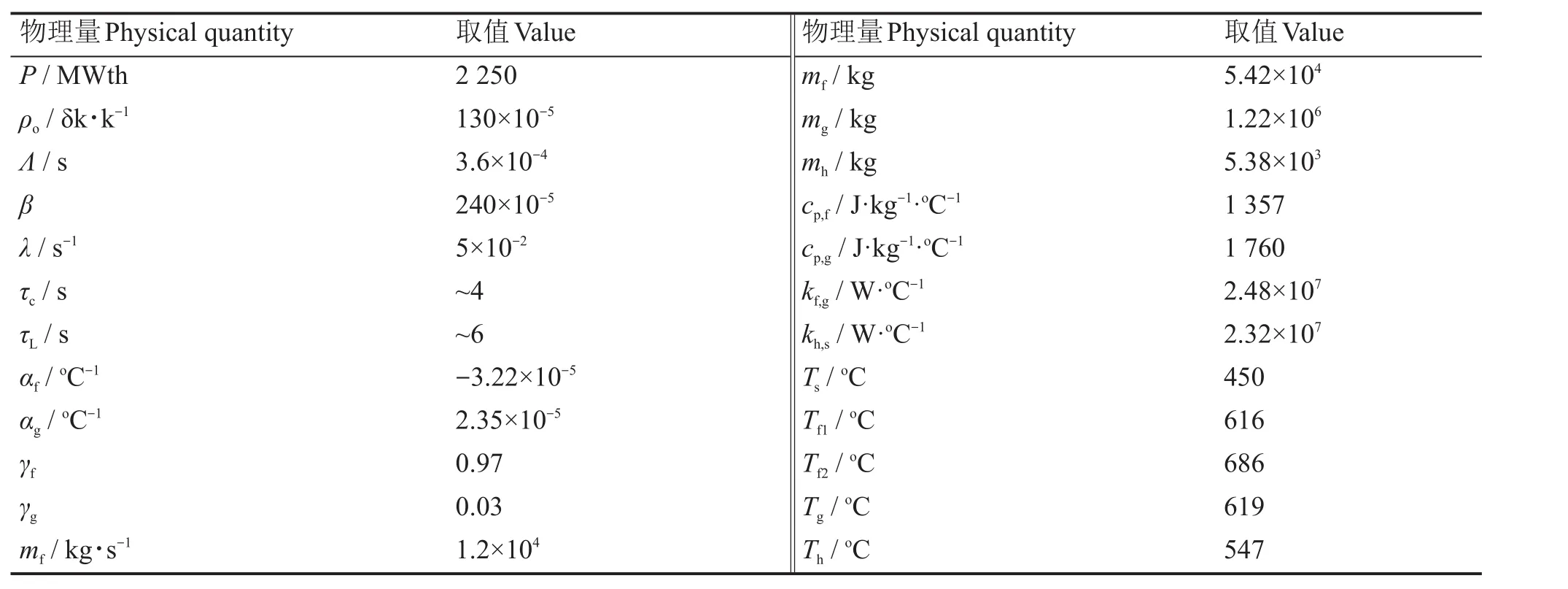
表1 石墨慢化熔盐堆参考数据[5]Table 1 Data referenced for the graphite moderated WSR[5]
2 模型变换
要设计控制器,有必要对模型进行简化。在本节中,给出了基于该堆芯模型推导功率二阶微分方程的详细过程。
首先,由式(1)、(2)可知:
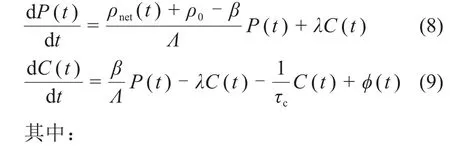

式(8)中ρnet为合成反应性,由外部反应性ρext及热反馈反应性ρth决定:

式中:αh为控制棒微分价值;h为控制棒的插入长度。
ρth由式(13)确定:
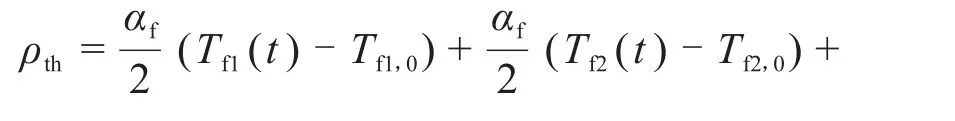

αf、αg分别为燃料结点和石墨结点的反应系数。又由对堆芯建立的1G-2F热力学模型式(3)、(4)、(5)和(6),开始二阶微分方程标准型的推导:根据二阶微分方程的形式,方程最终化简为:

将式(8)对时间求导,得:


3 线性自抗扰控制器设计
现考虑具有未知动态和外部干扰的二阶状态方程形式[7]:

式中:y和u分别是被控制量和控制量;g是模型不确定因素;w为系统的外部扰动;a1、a2就是模型信息。
3.1 不加模型信息的线性自抗扰控制器设计
下面先考虑不加入模型信息的线性自抗扰控制器[8]。
将式(29)变换为:

其中:f代表扰动——模型未知的非线性时变动态扰动。
ESO最基本的思想就是得到fˆ,即f的观测值。
令:

式中:x为系统的扩张状态。
为此,假设f是可微的且

所以式(31)可写为:

增加了一个扩张状态x3=f,h=f·是未知的扰动。所以f就可以通过观测器状态空间估计出来了。
其中:
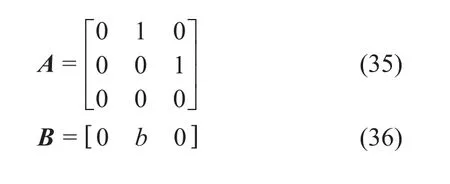
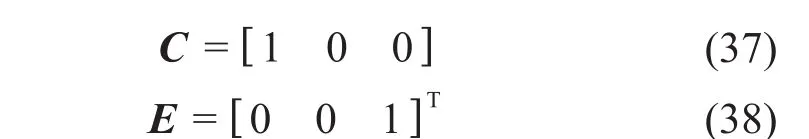
现在状态空间观测器就可以表示为LESO:

L是观测器增益矢量,可通过一些已知的方法例如极点配置法来得到其值:
为了方便起见,考虑观测器的三个极点都在ωo的一种特殊情况。所以ωo成为了观测器带宽和观测器唯一的整定参数。它所产生的特征多项式为:

通过对比得:

如果增益调整合适,观测器将会追踪到如下状态:
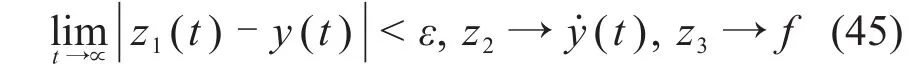
因此,ADRC能够通过消除使用f的观测值fˆ的影响来主动地实时补偿f。对于控制器来说,如果fˆ与f完全重合,那么控制器可以被设计成:

忽略z3的估计误差,那么控制器就变为一个单位增益的二重积分器:

类似于PD控制器,很容易来进行控制

式中:r是阶跃信号。-kdz2其原型为kd(r-z2),使用这种简化是为了避免式子中出现阶跃信号的微分形式,也为了使闭环传递函数的纯二阶控制器没有零项。所以纯二阶没有零项的闭环传递函数的形式为:

其中:kp=,kd=2ξωc。ωc是控制器带宽;ξ是阻尼比,用于减少波动,适当调节ξ可以使控制效果更好。一般地,ξ=1。
3.2 加入模型信息的线性自抗扰控制器设计
若a1和a2已知,则式(30)可写为:

状态方程形式仍为式(34)所示,根据式(50)有:

B、C和E不变。因此,线性扩张状态观测器可以被设计为:

其中:

uc是观测器组合输入:


L是观测器增益矢量[8]:

同样用一个PD控制器来控制
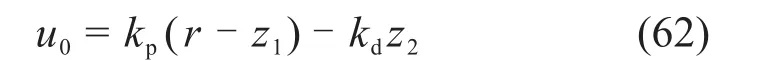
纯二阶没有零项的闭环传递函数形式与式(49)一致:

其中:

控制器的结构如图2所示。
4 仿真结果
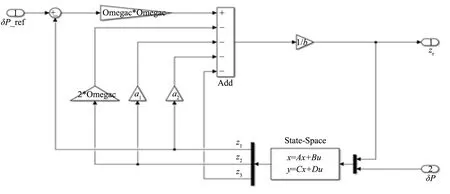
图2 线性自抗扰控制器结构图Fig.2 Structure diagram of LADRC
系统仿真是在MATLAB/SIMULINK®环境下实现。在此,线性自抗扰控制器的观测器和控制器参数由ω0和ωc来确定。
然而,必须在观测器跟踪状态的速度和对实际参数整定中观测器对噪声的敏感度之间作出折中。对于控制器带宽ωc,ωc越大,系统的响应速度越快,抗扰效果和对参数变化的敏感度更好,但同时随着稳定性的降低,带来了更严重的振荡和超调。对于观测器带宽ω0,ω0越大,线性扩张状态观测器的观测精度就更高,对传感器噪声的敏感度越大。因此,ω0应从一较小值开始逐渐增大,直到其观测精度符合要求[9]。
综合考虑控制效果与控制代价,经过模型调试和参数整定后,本文中取ωo=5,ωc=6。
以下仿真结果均是加入模型信息的自抗扰控制器的控制结果。
4.1 控制性能分析
做三组仿真实验,令系统在2 s时熔盐堆的相对功率Pr阶跃下降10%,即由100%阶跃下降到90%、由50%阶跃下降到40%、由25%阶跃下降到15%,三种阶跃变化下控制性能分析。
仿真实验结果如图3~5所示。
由以上仿真结果分析可知,线性控制器在5 s内便使反应堆功率达到稳定。说明对于熔盐堆的功率控制,采用LADRC系统是可行且有效的,且其调节速度和平稳程度比较高,超调量很小。
再做一组仿真实验,令系统在3 s时熔盐堆的相对功率Pr由100%阶跃下降到90%,堆芯平均温度变化如图6所示。
由仿真结果分析可知,线性控制器在1 000 s内可以使反应堆堆芯平均温度达到稳定。
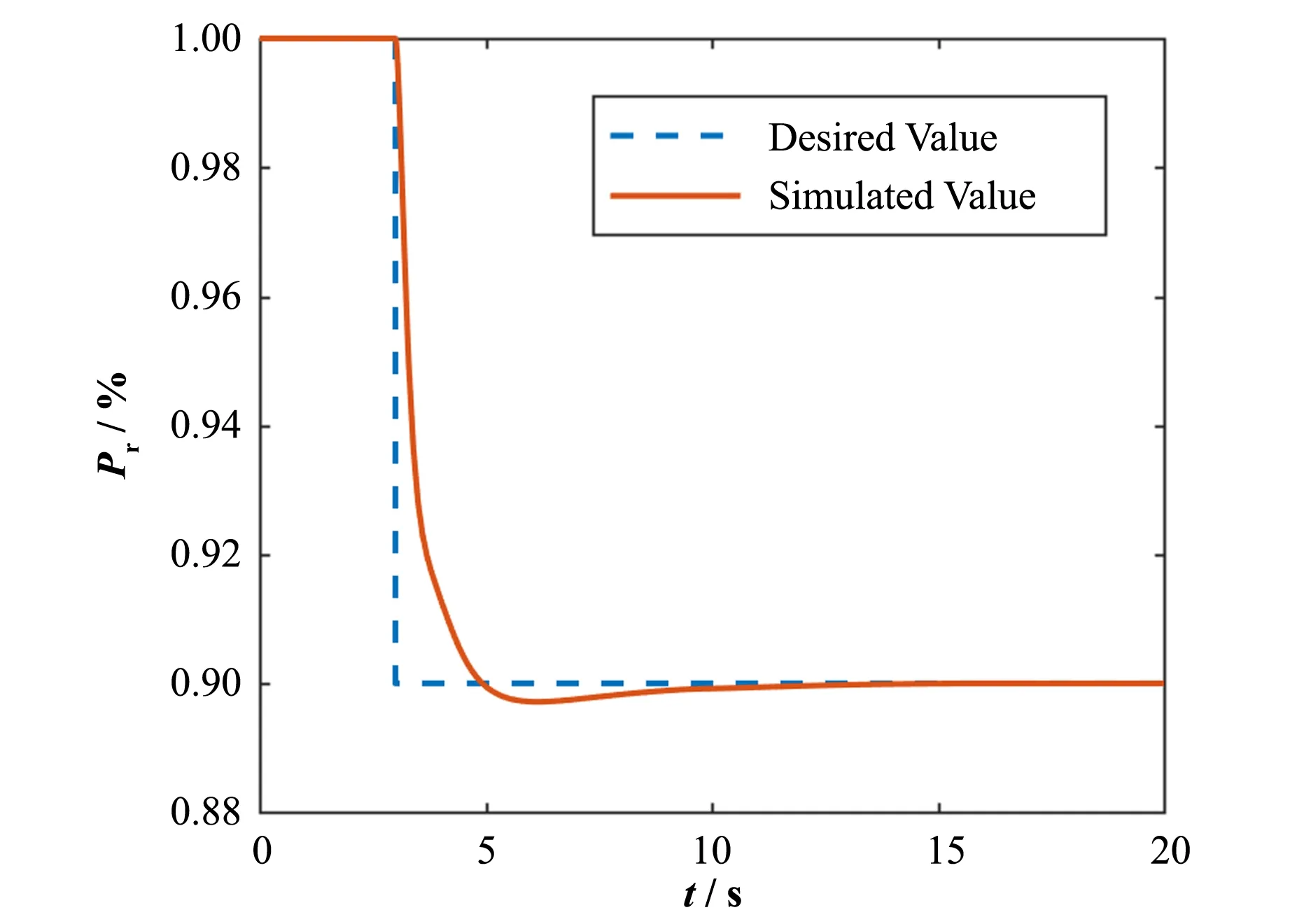
图3 相对功率从100%阶跃下降10%的响应Fig.3 Responses of the relative power step decreasing from 100%to 90%

图4 相对功率从50%阶跃下降40%的响应Fig.4 Responses of the relative power step decreasing from 50%to 40%
4.2 抗扰效果验证
为了验证所设计控制器的抗扰效果,在第3 s时加入20×10-5的反应性阶跃扰动,系统响应如图7所示。
由仿真结果可知,在第3 s时加入20×10-5的反应性阶跃扰动,系统快速响应,并且在3 s内达到稳定。
在第3 s时加入20×10-5的反应性阶跃扰动,堆芯平均温度变化如图8所示。
由仿真结果可知,在第3 s时加入20×10-5的反应性阶跃扰动,堆芯平均温度在3 s内达到稳定。
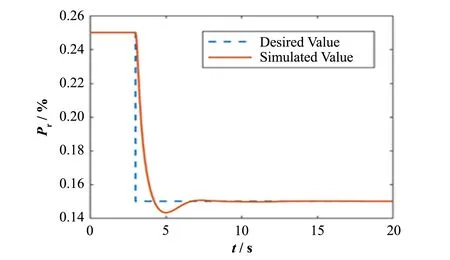
图5 相对功率从25%阶跃下降15%的响应Fig.5 Step responses of the relative power decreasing from 25%to 15%
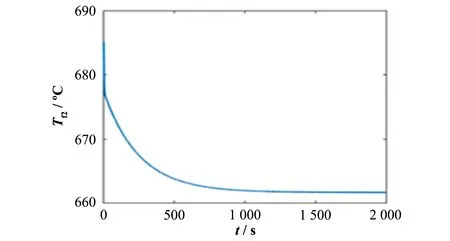
图6 相对功率从100%阶跃下降10%引起的堆芯平均温度变化Fig.6 Change of average core temperature caused by the relative power step decreasing from 100%to 10%

图7 20×10-5反应性阶跃增加扰动的响应Fig.7 Response of 20×10-5reactivity step increase disturbance

图8 20×10-5反应性阶跃增加扰动引起的堆芯平均温度变化Fig.8 Change of average core temperature caused by 20×10-5reactivity step increase disturbance
冷却剂流量给定值阶跃下降10%后,系统响应如图9所示。
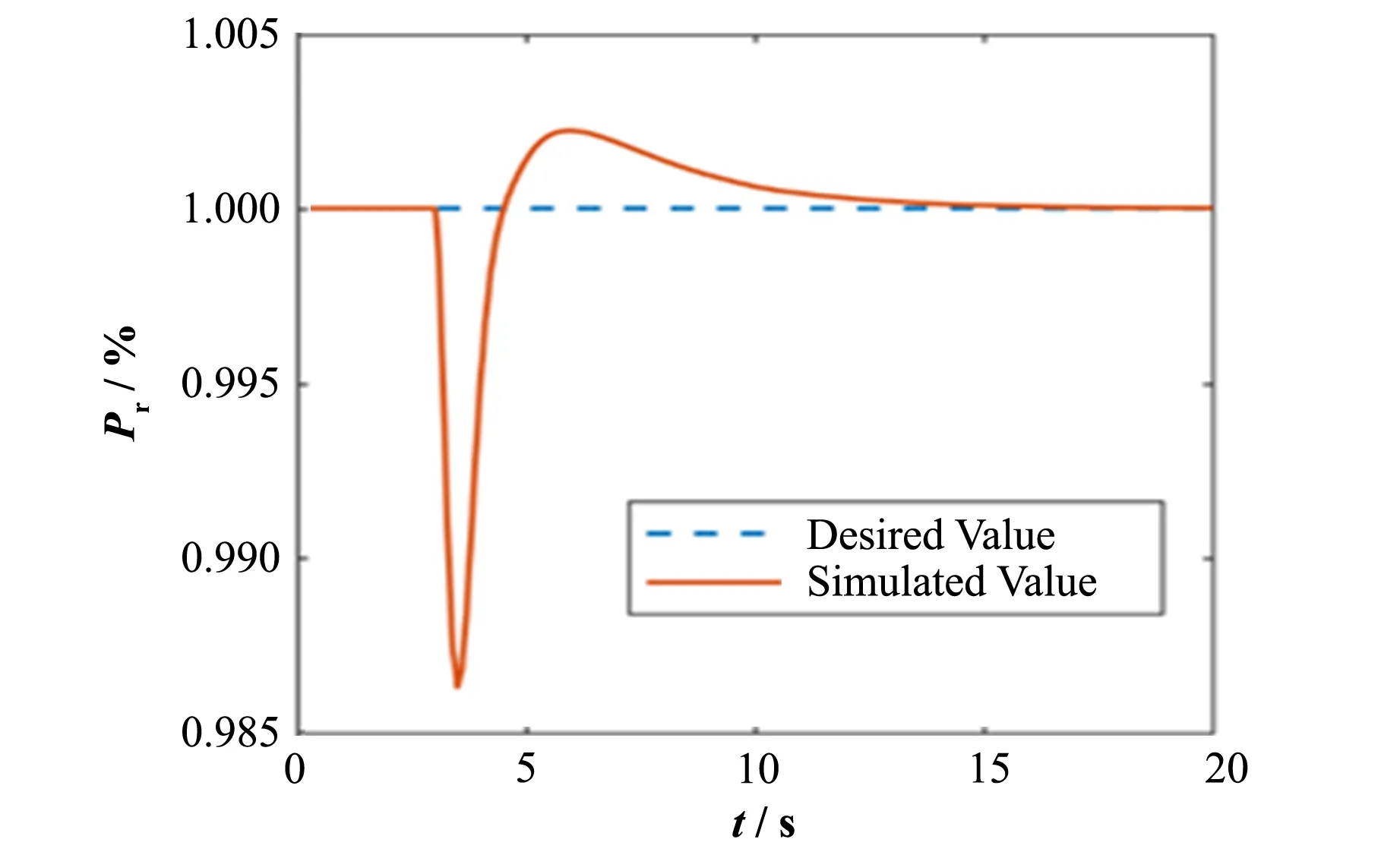
图9 10%冷却剂流量下降阶跃扰动的响应Fig.9 Response of 10%coolant flow decreasing step disturbance
由仿真结果可知,在冷却剂流量给定值阶跃下降10%后,系统响应迅速,并且在10 s前趋于稳定。
冷却剂流量给定值阶跃下降10%后,堆芯平均温度变化如图10所示。
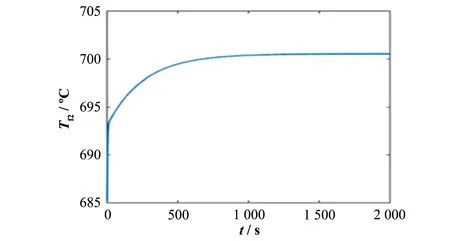
图10 10%冷却剂流量下降阶跃扰动引起的堆芯平均温度变化Fig.10 Change of average core temperature caused by 10%coolant flow decreasing step disturbance
由仿真结果可知,在冷却剂流量给定值阶跃下降10%后,堆芯平均温度在800 s前趋于稳定。
冷却剂入口温度给定值阶跃下降10%后,系统响应如图11所示。

图11 10%冷却剂入口温度下降阶跃扰动的响应Fig.11 Response of the coolant inlet temperature with 10%decreasing step disturbance
由仿真结果可知,在冷却剂入口温度给定值阶跃下降10%后,系统响应迅速,并且在第10 s左右逐渐趋于稳定。
冷却剂入口温度给定值阶跃下降10%后,堆芯平均温度变化如图12所示。

图12 10%冷却剂入口温度下降阶跃扰动引起的堆芯平均温度变化Fig.12 Change of average core temperature caused by 10%coolant inlet temperature decreasing step disturbance
由仿真结果可知,冷却剂入口温度给定值阶跃下降10%后,堆芯平均温度在1 200 s前趋于稳定。
当线性自抗扰控制器的观测器和控制器采用上述参数时,对于观测引入的白噪声(功率5 W),仿真结果如图13所示。

图13 测量噪声对控制性能的影响Fig.13 Influence of white noise on the system control performance
由仿真结果可知,系统对于噪声不敏感。
在5 s时冷却剂流量降低10%,冷却剂入口温度下降10%,并引入20×10-5反应性,系统响应如图14所示。
由仿真结果可知,在冷却剂入口温度给定值阶跃下降10%,在冷却剂流量给定值阶跃下降10%和加入20×10-5的反应性阶跃扰动后,系统响应迅速,并且在第10 s左右逐渐趋于稳定。
对以上所有仿真结果分析可知,设计的控制器对测量噪声不敏感,且当外界发生阶跃变化时,系统反应迅速并且趋于稳定。因此,设计的控制器抗扰性能良好。

图14 10%冷却剂流量、10%冷却剂入口温度阶跃扰动和20×10-5反应性阶跃增加扰动的响应Fig.14 Response of step disturbances caused by 10%coolant temperature decrease,10%coolant flow decrease and 20×10-5reactivity increase
5 结语
从熔盐堆堆芯的非线性模型推导出了带有总扰动项的二阶微分模型。基于该模型,设计了线性自抗扰控制器来控制熔盐堆堆芯功率。综合考虑控制效果,经调试整定了控制器和观测器的带宽参数。仿真结果表明,所设计的自抗扰控制器具有调节速度快、超调小、抗扰和噪声抑制能力强,综合性能优异。
