三翼钻头钻进过程模拟及结构参数优化

陈佳蕊，周翠红，冯利华

1北京石油化工学院机械工程学院 北京 102617

2中铁一局集团第二工程有限公司 河北唐山 063000

反 循环钻机具有广泛的适应性，既可在狭窄场地或隧道内施工，又可在市中心繁华地段施工。在钻孔灌注桩施工过程中，大直径钻机钻头部分质量加载于刀具处，刀具压入地层后钻杆带动钻头旋转破碎[1]。

钻头的钻进过程是非常复杂的非线性过程，李鹏等人[2-4]使用有限元软件对钻头破岩过程及流场进行了优化设计。杨成等人[5]针对砂卵石地层，运用Abaqus软件模拟优化了不同结构参数钻具模型。受设备、地质影响，在地质情况较为复杂的条件下进行钻孔灌注桩施工，存在钻孔施工难度大、砂卵石地层施工进度缓慢等问题[6]。

将非线性有限元的分析方法运用到钻头钻进过程中，并对钻头结构进行优化可以提高钻机的钻进效率。研究中结合灌注桩机械成孔施工现场，对三翼钻头钻进不同地层的过程实现显式学的动态过程模拟，探究反循环钻机钻进不同地层的工况，并利用均匀试验法优化钻具参数，为提升反循环钻机钻进效率提供了依据。

1 模拟方法

1.1 钻进过程分析

在钻头钻进地层的过程中钻头与地层间相互作用，在钻杆施加向下轴向压力的同时，钻头进行旋转以切削周围的地层，其受力分析如图 1所示。受钻压和钻速的影响，当钻头的轴向压力与切削力大于地层的承受能力时，地层发生疲劳破坏。

图1 钻头切削受力分析Fig.1 Force analysis of drilling bit

1.2 建立物理模型

建立钻头与不同地层的三维实体模型后，使用ANSYS Workbench中 Explicit Dynamic模块进行数值模拟，对钻头钻进不同地层的动态过程进行仿真，涉及的地层模型属于规则的面和体，可以利用自适应网格划分的方法来得到合理的网格，减少模拟时间。根据不同地层等效塑性应变速率的情况，研究钻进过程中钻进参数、钻头结构对钻进效果的影响。

结合工程实际，模拟建立的物理模型分为钻头和地层 2种结构。因砂卵石地层较难钻进，因此设置单一层砂卵石地层模型厚度为 300 mm，边长为 1 800 mm的立方体，整体结构如图 2所示。钻头在钻进过程中可能遇到多种不同种类地层，因此选取典型地层(粉质黏土层、细中砂层、砂卵石层) 综合建立多地层模型。

图2 三翼钻头与地层三维模型Fig.2 3D model of three-wing bit and stratum

在岩石底部设置固定约束条件，暂不考虑周围砂卵石压力的影响。砂卵石、粉质黏土层、细中砂地层的本构模型参数设置如表 1所列。钻头设置为刚性，弹性模量为 860 000 MPa，泊松比为 0.3，密度为 7 800 kg/m3。模拟设置主要包括：在连接模块中添加运动副，选择 Body-Ground菜单中的圆柱副Velocity，方向竖直向下，大小为 0.27 m/s。添加旋转圆柱副 RotationalVelocity，顺时针方向，大小为 2～ 10 rad/s。分析设置中定义载荷步数的结束时间为 0.5 s，reference energy cycle为 1 000 000，单一地层设置边界条件作用于地层的下底面，为防止多地层被钻头带动而旋转，多地层设置边界条件作用于地层的下底面与4个侧面。

表1 本构模型参数Tab.1 Parameters of constitutive model

1.3 网格划分

由于钻头钻进过程情况复杂，网格划分可能会出现不合理现象，过密的网格会出现局部转矩过大引起的形变现象，因此需要对网格质量进行检查。网格划分共分为 2部分，对钻头采用 Workbench四面体网格自动划分方式。在处理岩石网格时，为提高模拟精度，首先对岩石上底面和下底面的 8条侧边添加尺寸控制，并调整网格尺寸，偏差类型选择向中心靠拢，靠齐系数为 10.0，使整个岩石的网格中心部分密集。钻头与地层相互作用中心点的网格划分较密、四周网格划分较疏，多地层 (粉质黏土层、细中砂层、砂卵石) 的网格划分方式与砂卵石地层相同，选用的网格数为 56 342。

2 钻进过程模拟及分析

2.1 钻进过程模拟

对 3类地层进行钻进过程模拟以研究不同地层的钻进效果与钻进效率，钻进过程如图 3所示。

粉质黏土层的 0.2 s和 0.5 s时的钻进过程如图3(a)、(b) 所示。随时间增长，粉质黏土层的地层单元格逐渐破坏。由于粉质黏土层的钻进难度低，所以等效塑性应变随时间增长较快。

细中砂层 0.2 s和 0.5 s时的钻进过程如图 3(c)、(d)所示。由于细中砂地层颗粒间无内聚力、性质松散，细中砂地层的钻进效果与粉质黏土层钻进效果有很大不同，这是由细中砂地层本构参数及本身性质决定的。细中砂地层的等效塑形应变增随时间增长缓慢。

图3 钻进过程Fig.3 Drilling process

砂卵石地层 0.2 s和 0.5 s时的钻进过程如图 3(e)、(f) 所示。钻头在钻进砂卵石地层过程中，受钻压与转矩的共同作用，砂卵石层所受应力逐渐增大，由弹性变形至塑性变形，达到某一临界值后砂卵石层单元格逐渐破坏，随着时间增长，砂卵石层等效塑性应变持续增大。

2.2 钻进过程分析

平均等效塑形应变如图 4所示。根据计算平均等效塑性应变可看出不同地层的等效塑形应变随时间的增加而增大。

钻进不同地层的钻进效果与钻进效率差异较大，细中砂地层的等效塑性应变较小，这是由细中砂松散的性质决定的。粉质黏土层的钻进效率较高，网格位移量较大，粉质黏土层的等效塑性应变远大于细中砂地层和砂卵石地层的等效塑性应变，表明粉质黏土层钻进难度更低。随着时间增加，砂卵石层等效塑性应变虽稳定增大，但砂卵石地层的钻进效率较低，需要优化钻头结构参数以提高砂卵石层的钻进效率。

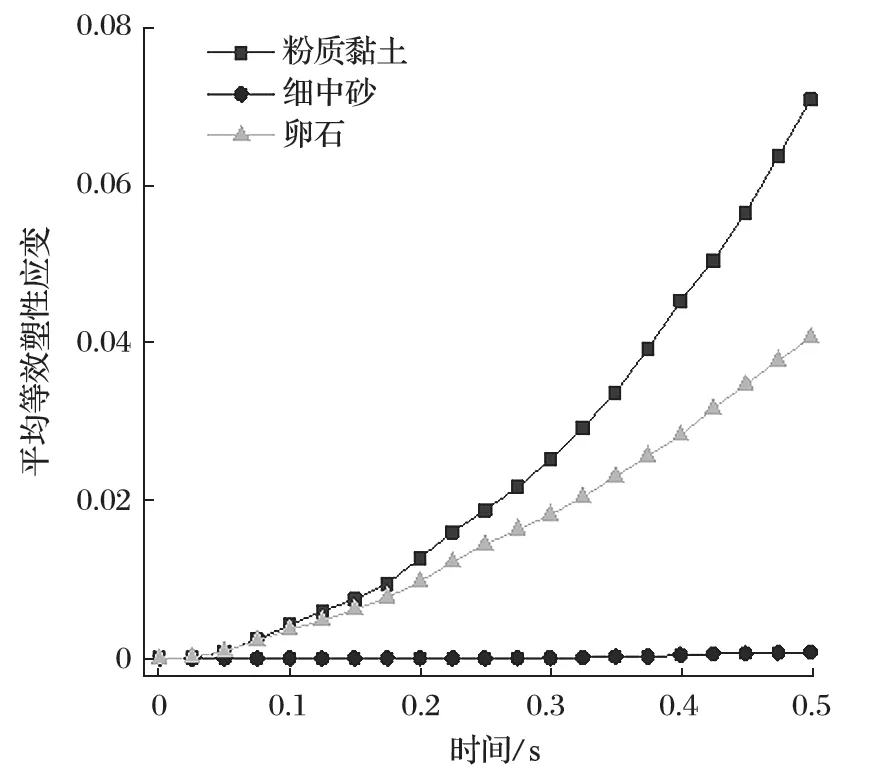
图4 不同地层平均等效塑形应变Fig.4 Average equivalent plastic strain of various stratum

3 均匀试验设计与优化

3.1 均匀试验

采用均匀试验法可以对钻头钻进模拟进一步优化，利用均匀设计表进行设计优化，最终确定模型方程和最佳砂卵石层钻进效率的钻头模型结构参数。

选择钻齿角度X1、钻齿与护壁夹角X2、钻齿直径X3、转速X4进行均匀试验。根据等效塑性应变速率得出不同影响因素对钻头钻进过程及钻进效率的影响，以期通过改变钻头结构参数及转速提高钻头的钻进效率。

按照 4因素 9水平试验的均匀设计表对砂卵石地层进行钻进过程模拟，并进行 9次模拟试验。均匀试验数据如表 2所列。依据模拟计算出的等效应变速率数值大小来判断不同钻头参数的钻进效率。

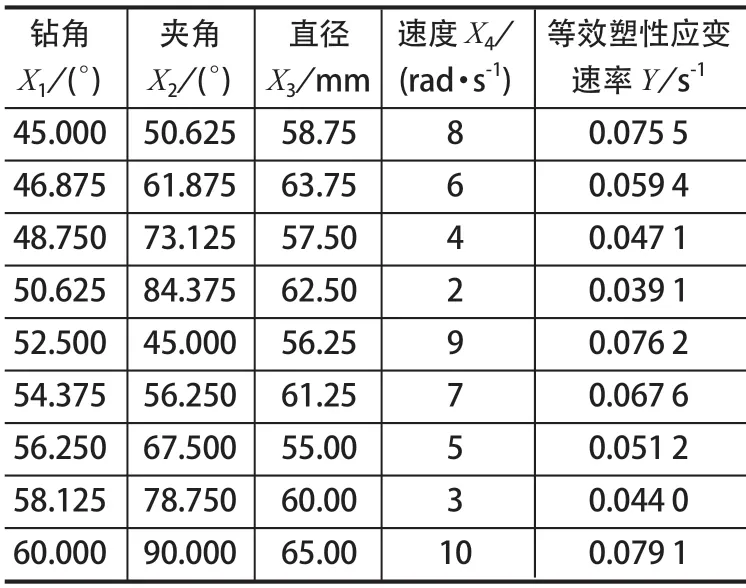
表2 均匀试验数据Tab.2 Dataof uniform test

3.2 回归分析与参数优化

钻角X1、钻齿与护壁夹角X2、直径X3和转速X4之间是相互独立的因素，根据均匀试验设计点分布原则，各因素间的相关性不应较高。因此对不同影响因素及其不同水平的数值进行相关性计算，各影响因素间的相关性系数范围为 0.1～0.5。计算影响因素与响应值之间最高相关性系数为 0.98，因此表明影响因素与响应值为线性关系，回归方程中不会出现二次项，则回归方程为

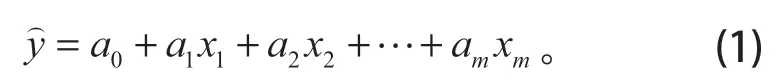
为方便分析使用 Minitab软件对均匀试验的结果进行回归分析，得到等效塑性应变速率的回归方程

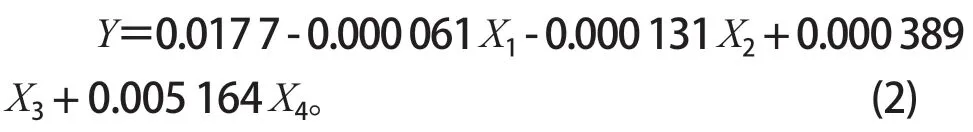
得到回归方程后需要对其进行检验，证实回归方程的可信度。根据 Minitab得出的方差分析表可知回归方程的F=72.01，查询F检验临界值表 (α=0.05)，可得F4,4(0.05)＝6.388。由于F＝72.01 ＞F4,4(0.05)＝6.388，这表示回归方程可信；P＝0.001＜0.05，表示回归方程显著；决定系数R2＝98.63%，这表明拟合度较高，因此可以使用该方程预测钻头钻进效率的最优模型结构。

根据得到的等效塑性应变速率回归方程，将不同影响因素X1、X2、X3、X4进行取值以便得到优化的最终结果。优化时目标函数的取值范围在约束函数内：

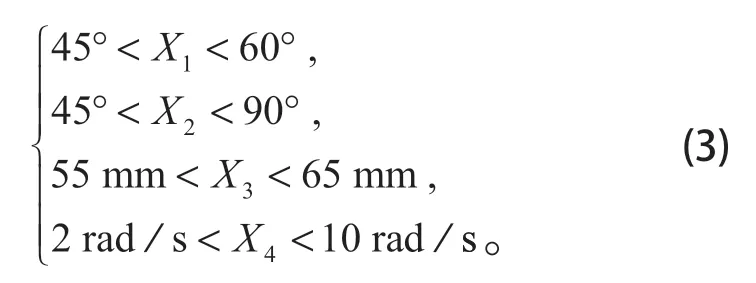
根据对比方差分析表中F值大小，可得到影响钻进效率的因素顺序为：转速、钻齿与护壁夹角、直径、钻齿角度。结合回归方程，得到最优解：X1＝45°，X2＝45°，X3＝65 mm，X4＝10 rad/s，此时目标函数最优值为 0.085 985。因此钻头的钻进效率最优参数：钻角为 45°，钻齿与护臂夹角为 45°，直径为 65 mm，速度为 10 rad/s。

4 结语

使用有限元模拟方法对三翼钻头钻进不同地层的动态过程进行模拟研究，计算平均等效塑性应变速率并比较不同地层的钻进效率，得结论如下。

(1) 随着钻进时间增加，地层所受平均等效塑性应变逐渐增大，不同地层的钻进效果与钻进效率差异较大，粉质黏土层的钻进效率大于细中砂地层和砂卵石层的钻进效率。

(2) 钻头钻进砂卵石层的过程中，砂卵石层所受应力逐渐增大，由弹性变形至塑性变形，当塑性应变达到某一临界值时，砂卵石层受到破坏，砂卵石层的等效塑性应变速率远小于粉质黏土层，砂卵石层钻头的钻进效率较低。

(3) 影响钻进效率的因素顺序依次为转速、钻齿与护壁夹角、钻齿直径、钻齿角度。