论匈牙利算法在仓储指派作业中的应用
2020-08-18朱传栋
朱传栋
(北京物资学院 北京 101149)
一、引言
在社会经营管理中,经常将人、物和事进行适当调配,以充分发挥人尽其才、物尽其用和事得其人的作用,提高管理效率。仓储作业中也是如此,对于一批入出库任务,如何指派入出库作业效率最高,能够使得总费用最少,这是一项典型的分配问题。以U形多道式仓储系统为例,其模型的特殊性,一般都采用特殊的解法——匈亚利算法,其也是目前指派问题求解方法中应用最广泛的解法。
二、匈牙利算法解决指派问题的基本思想
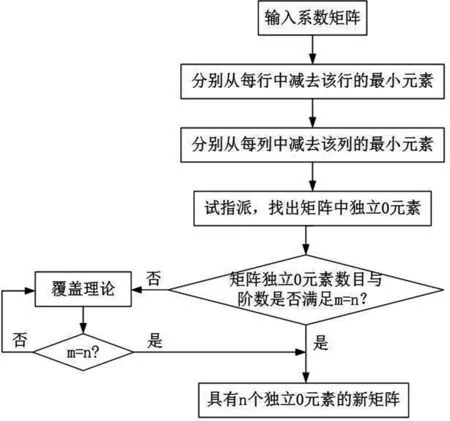
图1 匈牙利算法流程图
算法原理如下:C=(Cij)n·n为研究问题的目标系数矩阵,且满足Cij≥0,首先需对每行/列元素减去该行/列最小元素,得到n个具有不同行/列的独立0元素Cij,若独立0元素数小于矩阵阶数,进行覆盖操作,直到含有n个独立0元素,该方法得到的矩阵具有和原矩阵相同的最优解。其中,算法流程如图1所示。
三、货位分配优化方案
其中,物资存储采取就近货位分配和随机分配相结合的ABC货位分类方法,即在物资存储工作中,都存在“少数关键和多数一般”这种规律,少数重要可对系统起到决定性作用,多数一般甚至不大重要但又不可或缺。如果能够将重点工作用于解决这些少数但关键重要的事物上,对多数但一般重要事物进行一般管理,比起不分轻重同等对待,显然前者效果要好得多。ABC货位分类法,就是基于这种思想,并进行与之相应的管理。这里以入出库频率为主要指标,A类作业频率较高,较靠近入出库口;B类作业频率中等,距离一般;C类作业频率较低,距离较远。
所以,根据存储物资种类、特性及该系统运行特点,为集中巷道作业,提高堆垛机运行效率,需要对货架区进行货位分配优化。这里,不同于以往研究,即一巷道货架放部分A类物资和部分B、C类物资,将剩余A、B和C类物资安排在另一条巷道两排货架上,具体如下图所示。

图2 ABC货位分区安排示意图
四、匈牙利算法在具体指派中的应用
以某U型多道式仓储系统为研究对象,该系统货架共4排、30列(双货位货格)、12层,配有一台转弯型堆垛机,可管理两条巷道、四排货架。具体数据获取方面,货格规格为长1980mm*高925mm*宽1200mm。堆垛机直道阶段水平方向速度为vXmax=1.67m/s,水平方向加速度为aX=±0.3m/s2;垂直方向速度为vYmax=0.5m/s,垂直方向加速度为aY=±0.3m/s2。弯道阶段,为保证堆垛机安全,其水平方向速度较低且载货台降至较低位置,速度v弯=0.5m/s。ta、tb分别表示单一命令和复合命令作业巡回中包括定位、货位探测和货叉作业巡回等固定不变的时间总和,其中,ta=4s,tb=7.9s。进行换巷道作业时,为便于优化,不考虑堆垛机本身体积、直轨与弯轨间切换和转弯前载货台降至较低位置等因素对实验结果的影响。
表1为系统一初始任务单,作业位置(x,y,z)中x、y、z分别表示排、列、层。

表1 初始任务单数据
对任务单数据进行分析,平衡其入、出库货位数量,使入出库货位数量能够配对一致,其入出库货位之间运行时间如下表2所示。

表2 系统一组各入出库货位之间堆垛机运行时间(s)
由于复合作业作业效率较高,因此其仓储作业以复合作业为主,并基于ABC货位分配优化、集中巷道方式为前提进行的。这里运用Matlab编程,可得表3最优指派方案。

表3 最优指派方案
为提高系统运行效率,我们以集中巷道作业为前提,对上述最优指派方案进行排序,并假设以跨巷道作业组合中入库货位巷道为堆垛机所在巷道,对每一巷道进行入出库作业组合随机排序,并用跨巷道作业组合衔接,其中,系统一任务序列如下:4-0,7-6,1-2,9-3,5-8。优化前总作业完成时间432.58s,优化后总作业完成时间为223.13s,不考虑其他影响因素,系统优化前后效率能够提升45%以上。
五、结论
通过以上分析,可以得出以下结论:第一,合理进行货位优化能够提高系统运行效率;第二,复合作业较单一作业效率更高,利用匈牙利算法求解U形多道式仓储系统作业指派问题具有良好的效果。
