基于逆向工程的挠性机械臂三维动力建模研究
2020-08-18沈羽
沈 羽
(河南质量工程职业学院,河南 平顶山 467000)
1 引 言
上世纪80年代研究人员开发了三维动力建模技术之后,该技术很快就得到了普及。目前,世界上的工业大国均将三维动力建模技术作为大型机械生产中的核心环节[1]。现在,大型机械设计研究中最棘手的问题就是挠性机械臂设备的研究工作[2]。近些年,从我国机械专家对挠性机械臂设备的分析成果来看,笨重且结构复杂的挠性机械臂可以简化成针对其组成的5个基础零件的设计工作[3]。挠性机械臂的5个基础零件分别为底座、中部、大臂、小臂和手柄,其设计内容主要为位姿和速度等基本物理信息,从而构建出完整的挠性机械臂三维动力学模型,作为机械构造图应用到实际施工环节中[4]。
挠性机械臂的用途十分广泛,上到在宇宙空间站的建立、维护中发挥重要作用,下到在一个小型的机械生产中提高施工的工作效率。挠性机械臂有质量轻、跨度大、刚性低以及挠性大等特点,其模型结构相对复杂,不利于绘制。挠性机械臂生产中需要考虑的问题分为两大类:第一类是保证挠性机械臂内部零件的自身硬度,保证其在实时控制系统的强大压力作用下,可以稳定工作;第二类为如何搭配挠性机械臂零件,保证其达到最佳工作效率[5]。本文对如何提高挠性机械臂内部零件的自身硬度进行了有针对性的研究。
2 新型挠性机械臂三维动力建模方法
2.1 建立挠性机械臂运动学方程
新型挠性机械臂三维动力建模方法采用逆向工程的线性代数矩阵理论,建立挠性机械臂运动学方程[6,7],其基本运算流程如下:
第一,找出挠性机械臂中根据时间自变量而改变的运动学特征方程,假定系统中存在n个运动学特性方程,则其方程为:
f(t)=[f1(t),f2(t),……,fn(t)]
(1)
式中:f(t)为运动学特性方程;t为挠性机械臂的操作时间。
第二,利用矩阵代数的方法,描述机械臂各零件相对于基坐标系的几何关系。在该矩阵中,采用三角函数法来表示各零件之间的关系,通过矩阵来描述零件与整体之间的比例关系。
第三,应用正确的比例关系得到机械臂零件在运动过程中的转角变化情况,下面为挠性机械臂运动学问题简化成的等价3×3逆向工程的线性代数特色矩阵。
(2)
式中:T为挠性机械臂零件的矩阵特征值;θ为挠性机械臂零件运动时的转角大小;i为挠性机械臂中5个零件的编号,顺序为底座、中部、大臂、小臂、手柄,i=1,2,3,4,5。
2.2 建立挠性机械臂拉格朗日动力学方程
在完成挠性机械臂运动学方程的基础上,应用高等数学中的拉格朗日函数,来建立其动力学方程,依次计算出挠性机械臂所需动能和势能之间的数量关系,下面为主要应用的数学公式:
L=Ek-Ep
(3)
mg·d=F·H
(4)
(5)
(6)
式中:L为挠性机械臂所需动能与势能之间的插值;Ek为挠性机械臂所需动能;Ep为挠性机械臂所需势能;F为作用在挠性机械臂上的广义力;H为操作过程中挠性机械臂所提升的高度;qk为广义力所对应的力矩;v为广义力所对应的运行速度;q0为静止状态下的广义力矩;T为挠性机械臂运行一周期所用的时间;d为挠性机械臂的动力臂;m为挠性机械臂的质量;r为挠性机械臂的底座半径。
2.3 建立挠性机械臂三维动力模型
运用拉格朗日方程进行力学分析,对所设计的挠性机械臂中的力学特征有了精确的掌握之后,才能进入最后一步,即建立挠性机械臂的三维动力模型,其基本流程为:
第一,建立最基础的空间直角坐标系,即X轴、Y轴和Z轴。
第二,计算几个零件在3个坐标轴中的定值,其公式如下所示:
xi=aicosθi+dsinθi
(7)
yi=aisinθi+dtanθi
(8)
zi=vcosθi+atanθi+dsinθi
(9)
式中:xi为挠性机械臂中零件在X轴上的坐标;ai为挠性机械臂中零件运行时的加速度;θi为挠性机械臂零件运行时的转角大小;d表示机械臂的力臂;yi为挠性机械臂中零件在Y轴上的坐标;zi为挠性机械臂中零件在Z轴上的坐标。
第三,将Y轴沿自由度方向进行旋转,找到手柄所在的执行末端位置。
第四,在3个坐标轴上找到挠性机械臂中大臂和小臂所在的质心位点,并连接在一起。
第五,根据物理学知识精确找到底座和中部所在的坐标点。
第六,连接各坐标点进行绘图工作。图1为应用新型挠性机械臂三维动力建模方法得到的挠性机械臂模型图。
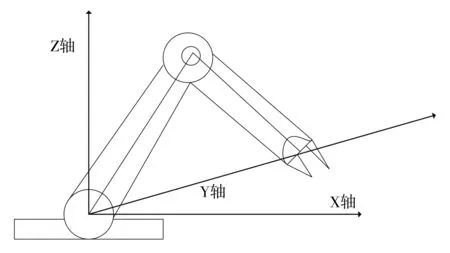
图1 挠性机械臂三维动力模型
3 仿真试验
3.1 试验准备
本试验利用新型挠性机械臂三维动力学建模方法与传统方法同时绘制挠性机械臂的动力学模型,采用计算机软件将两种动力学模型表达出来,参考实物从两个模型中挑选出5个相同的点,编号为1、2、3、4、5,判定新型方法的使用价值。
3.2 结果分析
表1为两个方法得到的挠性机械臂模型精确度对比情况。
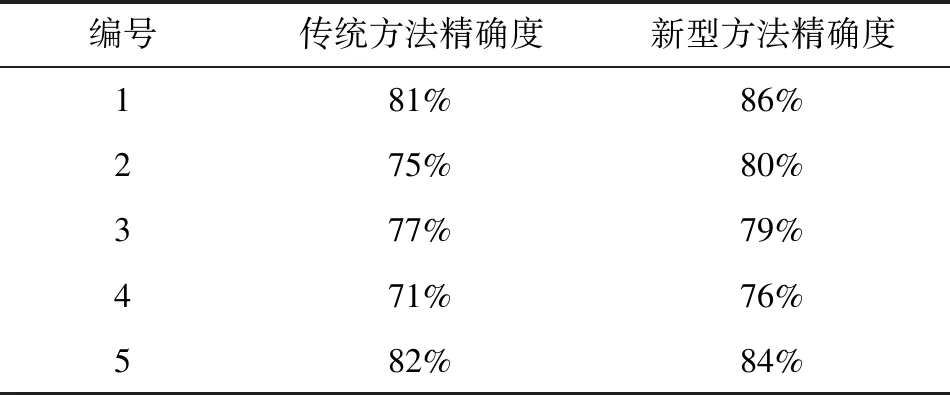
表1 两种方法构建出模型精确度对比结果
从表1可以清晰地看出,新型挠性机械臂三维动力建模方法设计出的挠性机械臂精确度平均值达到了81.0%,高于传统挠性机械臂77.2%的精确度平均值。因此,验证了新型挠性机械臂三维动力建模方法的使用价值。
4 结束语
如今,我国机械制造业的需求量日益增大,其中对挠性机械臂需求也越来越大。很多机械制造企业为了满足当前的市场需求,生产工作急于求成,造成大量挠性机械臂成品质量不合格。本文将线性代数理论和高等数学中拉格朗日运算理论引入到挠性机械臂的三维动力学模型的制作中,提高了当前挠性机械臂产品的质量。
