用材料力学方法分析悬臂叠层梁的应力及试验

吴 晓

(湖南文理学院机械工程学院，湖南 常德 415000)

1 引 言

为了提高梁的抗弯刚度，实际工程中经常把几根单梁通过螺栓、铆钉或销钉制作成叠层梁，这种叠层梁在机械工程、土木工程中得到了广泛应用。因此，材料力学、机械设计、钢结构等相关教材都对螺栓、铆钉连接的构件作了很大篇幅的阐述。《工程力学实验》教材[1]开发了综合性、研究性的材料力学教学试验，即悬臂叠层梁的应力试验。《材料力学》教材[2]也把悬臂叠梁作为习题。这些都说明了叠层梁作为承力构件，在实际工程应用中的重要性。本文为了解决、完善材料力学教材存在的问题，指出了文献[1]、文献[2]存在的不足，并对悬臂叠层梁的弯曲变形进行了理论分析。

2 问题的提出

由文献[1]可知，图1所示销钉连接悬臂叠层梁，其由两个尺寸、材料完全相同的矩形截面梁构成。

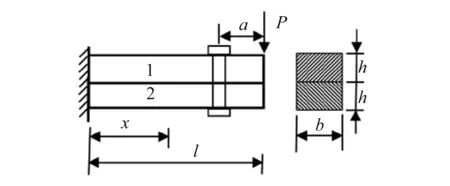
图1 销钉连接叠层梁

文献[1]中给出，a=30mm。为了后面计算分析，本文取图1所示悬臂梁的计算参数为：l=4m，b=20cm，h=20cm，P=30kN，E=210GPa。

文献[1]把图1所示销钉连接的叠层钢梁作为研究性的材料力学试验，认为销钉连接后，上、下两个梁趋于一个整体，会只有一个中性层。对此，笔者认为值得商榷。

文献[2]是螺栓连接的悬臂叠层木梁。当图1所示悬臂叠层梁的a=0时，即变为文献[2]中的悬臂叠层梁。文献[2]给出了悬臂叠层梁的计算参数：l=4m，b=20cm，h=20cm，P=15kN，E=10GPa，[τ]=80MPa。

文献[2]提出了两个求解问题：(1)两根梁连接成整体时，梁接缝上的剪应力τ及剪力T等于多少？(2)若两根梁用螺栓连接，试求所需螺栓的横截面积F。

当叠层木梁是一整梁时，由材料力学可知，木梁中性层处最大剪应力为：

(1)

式中，P为横截面剪力，b为梁宽，h为上、下层叠梁的梁高。

由式(1)可知，梁接缝上的剪力为：

(2)

由式(2)可知，所需螺栓横截面积为：

(3)

事实上，文献[2]给出式(2)、式(3)的结果是错误的。图1所示悬臂叠层梁是一次静不定梁，上、下叠层梁都存在轴力与梁截面弯矩的共同作用。而文献[1，2]把图1所示悬臂叠层梁作为整梁时，实际上默认了上、下叠层梁都不存在轴向力作用，梁横截面仅存在弯矩的作用。

3 叠层梁的弯曲分析

由材料力学可知，图2所示螺栓或销钉连接构件的横截面平衡方程为：

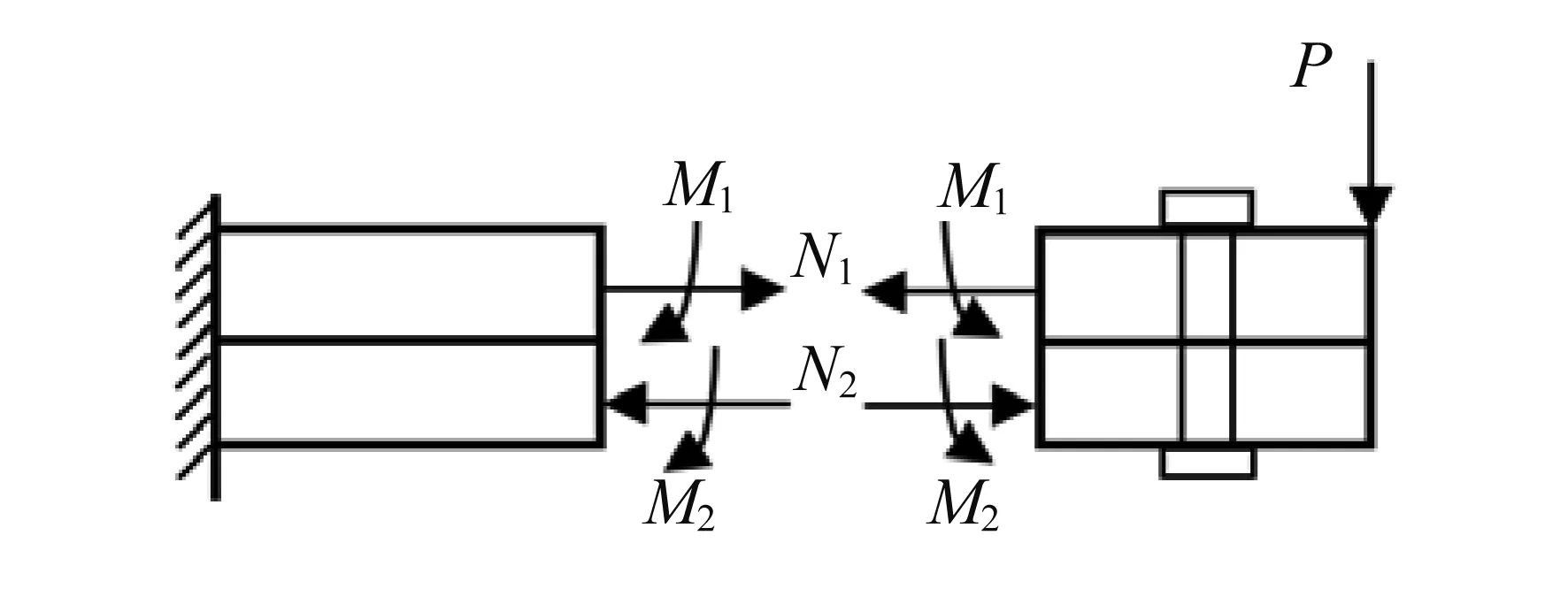
图2 叠层梁的内力

(4)

M1+M2+Nh=P(l-x)

(5)

由于图2所示螺栓或销钉连接的叠层梁在上下叠梁接触面的纵向伸长相等，可知：

(6)

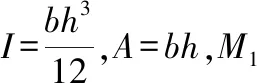
利用式(4)-式(6)可以求得：

(7)

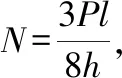
把式(5)写为如下形式：

M=M1+M2=P(l-x)-Nh

(8)

参阅文献[5]可知，在外载荷作用下，图1所示悬臂叠层梁的上、下叠梁各自弯曲时的微分方程分别为：

(9)

式中，D=EI，ρ为下层叠层梁弯曲时的曲率半径。

利用式(8)、式(9)可以得到上、下层叠梁横截面上的弯矩分别为：

(10)

(11)

利用式(7)、式(10)可得上层叠梁的上表面及下表面的弯曲正应力分别为：

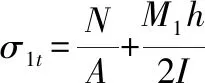
(12)

利用式(7)、式(11)可得下层叠梁的上表面及下表面的弯曲正应力分别为：

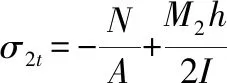
(13)

在式(12)、式(13)中，应力计算结果为正值时代表拉应力，应力计算结果为负值时代表压应力。

利用式(7)、式(8)，且令M=0，可求得：

(14)

当M>0时，由式(10)、式(11)可知：

M1>0,M2>0

(15)

结合式(12)、式(13)、式(15)可知，M>0时，上层叠梁上表面受到拉应力作用，下层叠梁下表面受到压应力作用。

当M<0时，由式(10)、式(11)可知：

M1<0，M2<0

(16)

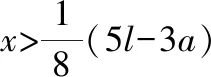
4 算例分析

以文献[1]销钉连接的悬臂钢质叠层梁为例，把有关参数代入式(12)、式(13)中，可得叠梁截面应力，具体数值见表1。把与文献[1]尺寸、材料相同的悬臂整梁截面最大拉应力与最大压应力列在表2中。

以文献[2]螺栓连接的悬臂木质叠层梁为例，把有关参数代入式(12)、式(13)中，可得叠梁截面应力，具体数值见表3。把与文献[2]尺寸、材料相同的悬臂整梁截面最大拉应力与最大压应力列在表4中。

假设文献[2]悬臂木质叠层梁上、下层叠梁之间光滑没有摩擦，可知螺栓受到剪力为：

(17)

由式(17)可知，所需螺栓横截面积为：

(18)

表2 钢质整梁应力MPa(a=30mm )

表4 木质整梁应力(MPa )(a=0)

由表1、表3可以看出，悬臂叠层梁上层叠梁下表面、下层叠梁上表面的应力皆不为0。所以，文献[1]把销钉连接的悬臂叠层梁作为整梁来考查梁应力试验是不成功的。因为，销钉或螺栓连接的悬臂叠层梁是一次静不定梁，而把销钉或螺栓连接的悬臂叠层梁作为整梁,则使销钉或螺栓连接的悬臂叠层梁变成了静定梁。

表3 木质叠梁应力(MPa )(a=0)

把式(2)、式(3)计算结果与式(17)、式(18)计算结果进行对比可知，两种方法计算结果不一致，式(17)、式(18)计算结果与文献[3]、文献[4]方法的计算结果相同，显然文献[2]的计算结果是错误的。

5 结束语

由以上分析可知：悬臂整梁弯曲凸起时，凸起的梁段上表面会受到拉应力，凸起的梁段下表面会受到压应力，这已成为材料力学教材中的常识。但是，自由端被螺栓或销钉连接的悬臂叠层梁，在外载荷作用下弯曲凸起时会发生一个反常现象，即在弯矩大的凸起梁段上表面受到拉应力、下表面受到压应力，而在弯矩小的凸起梁段上有可能是上表面受到压应力、下表面受到拉应力。计算分析表明，产生反常现象的原因，是悬臂叠层梁的上层叠梁轴向拉力与悬臂叠层梁的下层叠梁轴向压力形成力偶矩造成的。