基于变形机理分析的机翼前缘柔性蒙皮优化设计
2020-08-18吕帅帅王彬文
吕帅帅,王彬文,杨 宇
(中国飞机强度研究所 智能结构与结构健康监测研究室,陕西 西安 710065)
1 引 言
光滑无缝的机翼可变弯度前缘是一种新型的高升力装置。相比传统前缘缝翼,该机翼能够显著降低飞机起降阶段的气动噪声,并满足未来层流机翼对蒙皮表面光滑程度的苛刻要求[1-5]。
经过几十年的发展,逐渐形成了变弯度机翼前缘的基本设计方案[6-10],即通过内部机构驱动柔性蒙皮的纯弯曲变形,实现前缘下垂,其机构原理如图1所示。
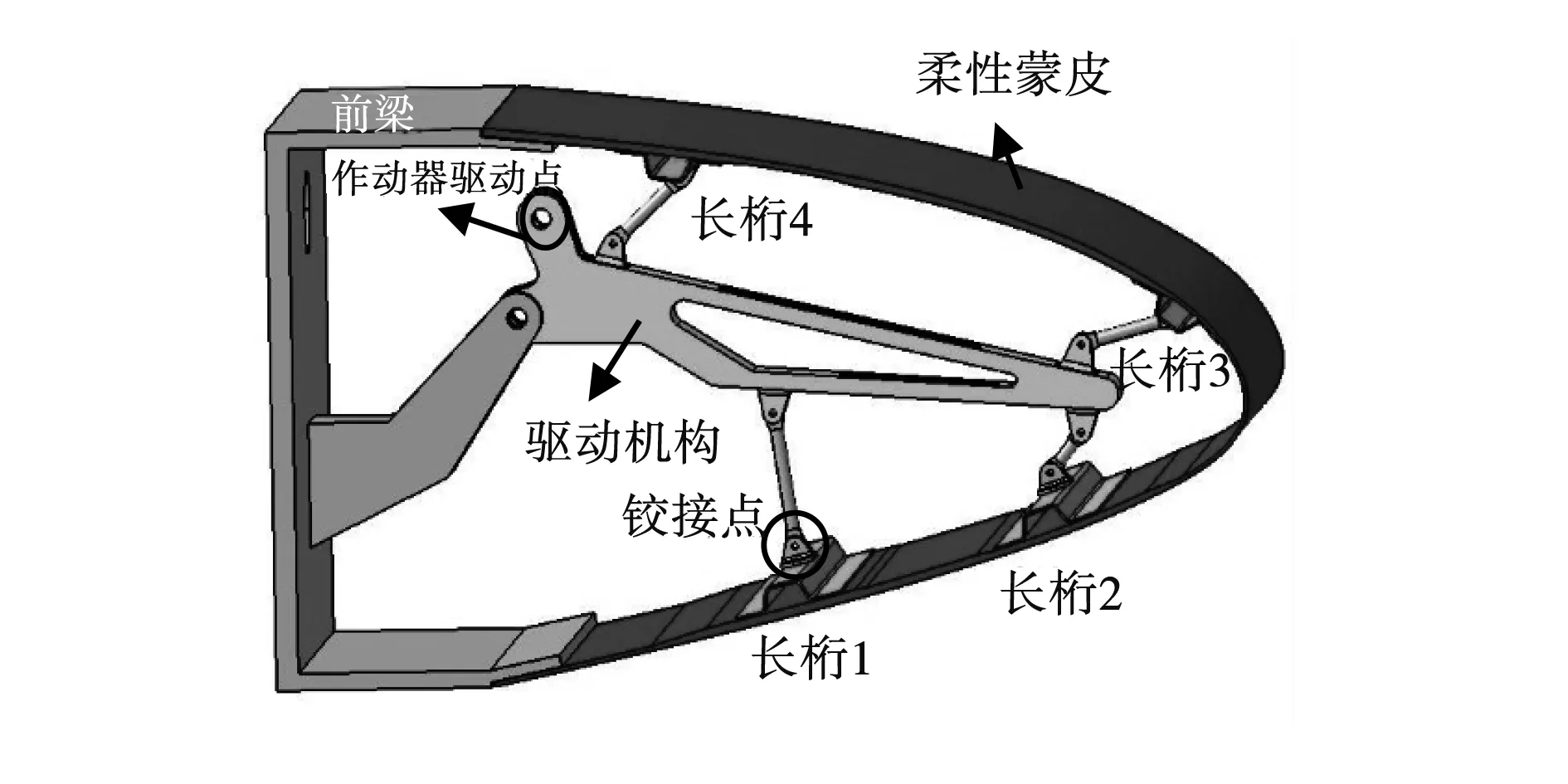
图1 变弯度前缘结构示意图
目前,对柔性蒙皮气动外形的考察主要包括巡航(初始翼型)和下垂(下垂翼型)两个状态。巡航状态的高精度气动外形是为满足自然层流机翼对蒙皮表面质量的苛刻要求,研究表明,即使是1mm的接缝高度差也会破坏层流[10]。下垂状态的精确变形则是为保证机翼的气动效率,前缘前端6mm的位移偏差可造成飞机的升阻比降低10%、升力降低4.5%。前缘的变形精度受多种因素影响,包括柔性蒙皮结构的变形误差、内部机构的驱动误差和加工组装误差等[6]。柔性蒙皮结构作为设计流程中的第一个环节,是影响变形精度的主要因素,因此必须保证柔性蒙皮变形的高精度。
为保证柔性蒙皮变形的高精度,现有设计方法通常是以下垂状态的高精度变形为设计目标,进行柔性蒙皮结构的优化设计,再对巡航状态的外形精度进行校核。由于柔性蒙皮的变形机理复杂、设计变量的数量多、变量约束范围的区间长度过大,优化结果难以同时实现变弯度前缘在巡航、下垂状态的高精度气动外形。
H. P. Monner在SADE(2009-2011)项目中采用处理多变量问题的分层优化策略对蒙皮结构进行设计,高耦合度变量的直接分层造成优化结果中上翼面产生较大的位移偏差,影响了前缘气流分布[11];Markus Kintscher等在SARISTU(2011-2015)项目中完善了柔性蒙皮结构的设计方法并进行了风洞试验,Kintscher采用单纯形法对结构参数进行同步优化,但由于单纯形算法处理多变量问题时易陷入局部最优解,最终优化结果在关键部位产生了8mm的位移偏差,造成前缘截面的曲率出现拐点,气动效能受到影响[6]。
中国飞机强度研究所的王志刚等人在Kintscher的基础上,使用带精英策略的非支配排序遗传算法(NSGA-II)实现了多类变量的协同优化设计,但设计变量过多、约束范围过大导致协同优化结果的变形精度只有小幅提高,最终在变形关键部位产生了近6mm的位移偏差,同样对机翼的气动效率产生较大影响[12]。
为此,本文提出一种柔性蒙皮结构的优化设计方法。该方法首先根据变形机理的详细分析将设计变量分别分为全局变量和局部变量、下垂精度控制变量和巡航精度控制变量。其次,在优化阶段,只针对下垂精度控制变量进行优化设计,达到减小全局变量数量、降低优化模型复杂度的目的,进而实现下垂状态的精确变形。再次,根据气动载荷分布,设计巡航精度控制变量,实现巡航状态的高精度外形。最后,以真实翼型为设计对象,使用本文方法和现有方法开展柔性蒙皮结构设计,对比两种设计结果在巡航、下垂状态的外形精度。
2 柔性蒙皮结构的设计变量分类
变弯度前缘柔性蒙皮结构包含蒙皮和长桁,其结构构型如图2所示。其中,蒙皮上下根部(边1和边2)为固支,以模拟前缘与机翼前梁的连接,参考点1~4则表示驱动机构与长桁的4个铰接点,驱动位移施加在参考点上。
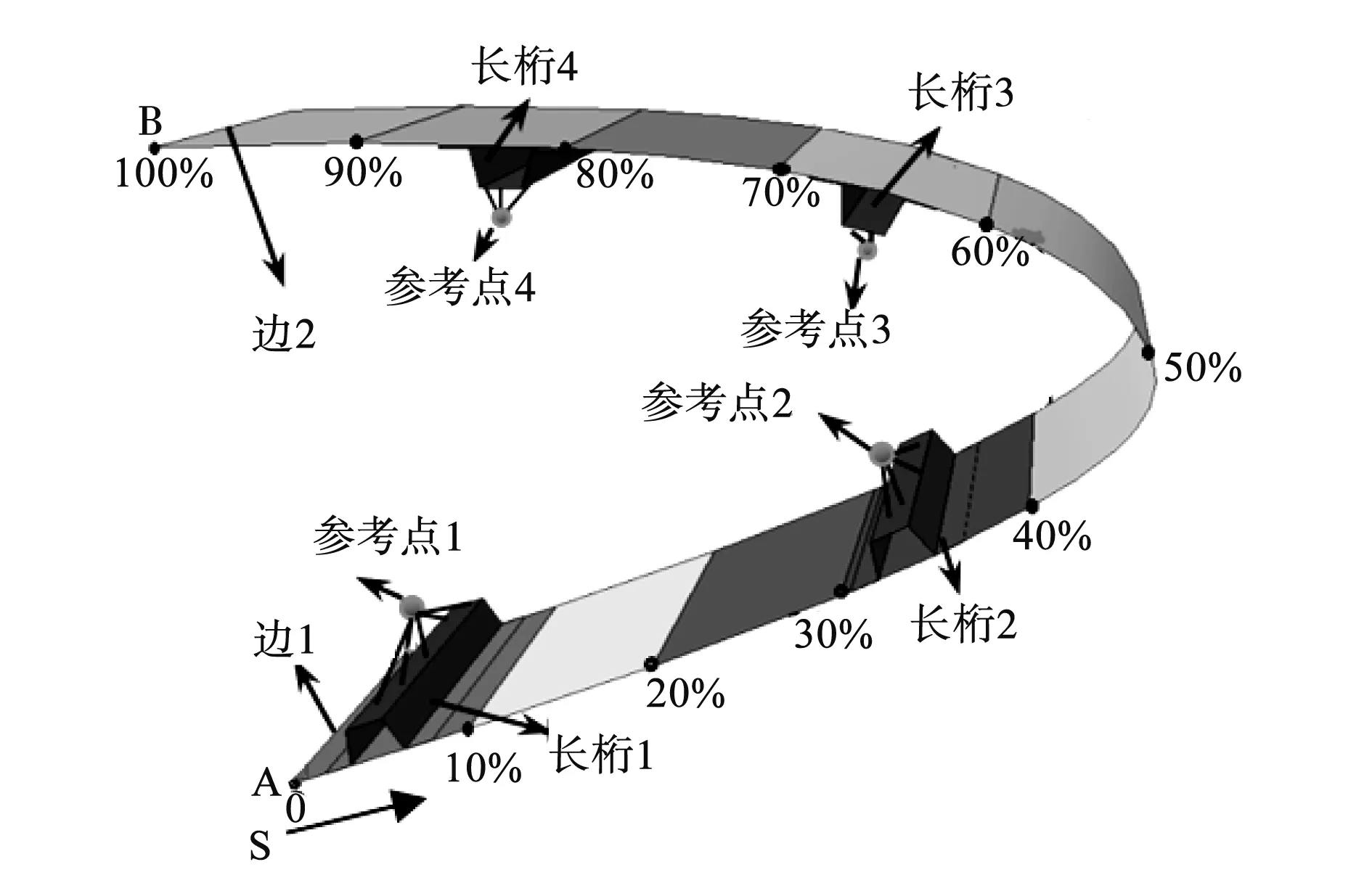
图2 后掠前缘柔性蒙皮的数值模型
柔性蒙皮结构的设计变量包括各设计区域的蒙皮厚度、长桁位置以及施加在驱动点处的驱动位移。
在翼型截面内建立归一化长度坐标S,规定可变弯度部分的下翼面端点A处S=0,上翼面端点B处S=100%,曲线AB上任意点C的S坐标为曲线AC与曲线AB的长度比值,如图2所示。在面向工程应用的研究中,柔性蒙皮通常采用玻璃纤维增强复合材料(GFRP)。
2.1 全局变量和局部变量
柔性蒙皮在下垂状态的变形形状由3类设计变量共同决定,根据3类设计变量对变形形状的影响程度,可将其分为全局设计变量和局部设计变量。全局变量是指在气动载荷保持不变的情况下,改变其数值,将影响整个前缘的变形形状,而局部变量是指改变其数值时,只影响柔性蒙皮的局部变形结果。长桁位置和驱动位移为柔性蒙皮结构的全局变量,而蒙皮刚度分布为局部变量。
该变形特征可通过图2中柔性蒙皮模型的变形来说明。首先为该柔性蒙皮结构赋予任意一种结构状态并将其定义为基准模型,然后对基准模型的结构按以下3种形式进行更改:①只更改长桁2的位置;②只更改长桁2的驱动位移;③只更改长桁2、3间蒙皮的刚度分布。经过数值模拟计算,3种更改模型与基准模型的变形结果对比如图3所示,改变长桁位置和驱动位移的模型与基准模型在前缘大部分位置都存在变形差异,而改变刚度分布的模型与基准模型只在长桁2、3间存在变形差异。该现象说明,一个长桁的位置和驱动位移能够影响前缘的整体变形结果,而局部刚度分布只影响局部变形结果。因此,长桁的位置和驱动位移决定了前缘下垂的角度和整体形状,蒙皮的刚度分布状态决定了各长桁间外形的精确度。
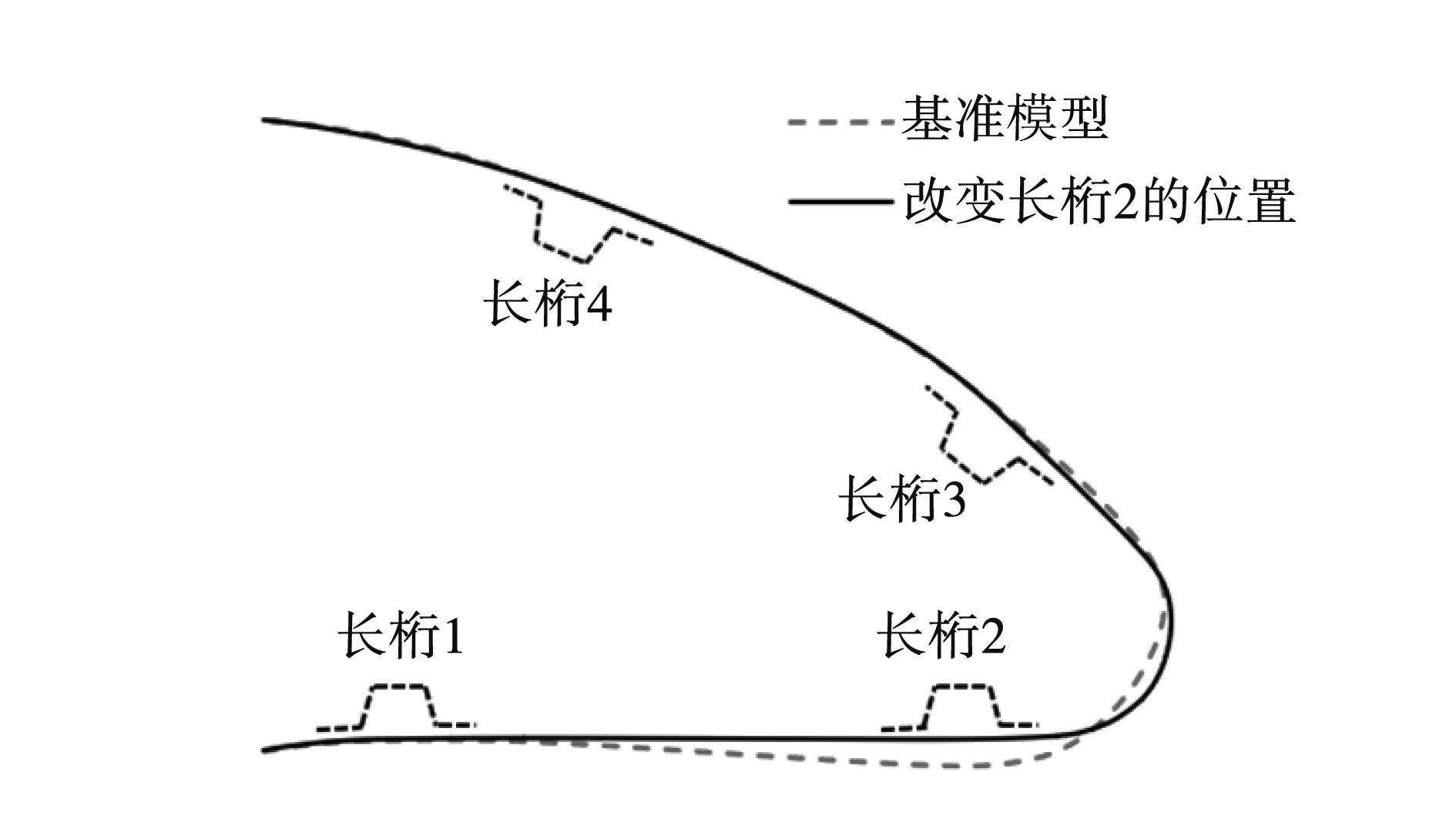
(a) 改变长桁位置模型和基准模型的变形形状对比

(b) 改变驱动位移模型和基准模型的变形形状对比
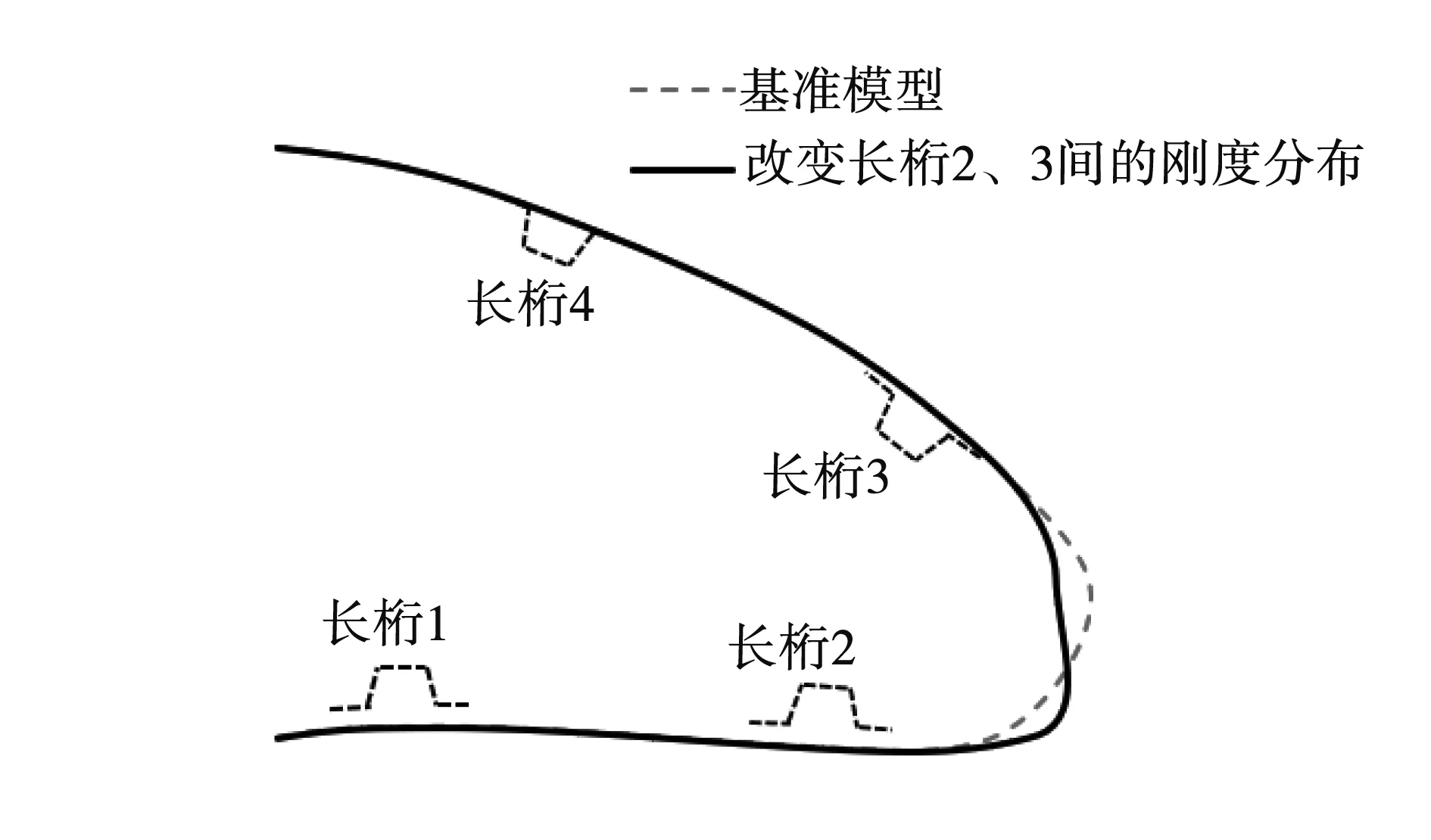
(c) 改变局部刚度分布模型与基准模型的变形形状对比图3 3种更改模型与基准模型的变形结果对比
2.2 下垂精度控制变量
现有设计方法中,驱动长桁的个数一般设置为4个,其中上、下翼面各两个。4个长桁位置和对应的8个(4×2)驱动位移均为全局变量,任何一个变量的改变都会对变形精度产生较大影响,进而增加了优化设计的难度。
然而,由于前缘的气动载荷较小,且GFRP的刚度较大,通过研究发现,驱动长桁的个数主要由柔性蒙皮变形前、后的曲率及其变化决定,而通常3个驱动长桁即可实现柔性蒙皮的精确变形,其中下翼面2个,上翼面1个。
图4所示为典型的柔性蒙皮曲率分布曲线。上翼面的初始曲率近似为0,曲率变化平缓、单调,在不考虑气动载荷情况下,将前缘在S=60%处分割,可将上翼面近似看作S=100%处为固支,S=60%为自由端且施加集中力的悬臂梁。

图4 典型初始曲率、目标曲率及曲率变化曲线
对于长度为l的等截面悬臂梁,在自由端施加垂直于轴线的集中力F并产生挠度Y,则悬臂梁轴线上距固定端x处的位移s为[13]:
(1)
做归一化处理:
(2)
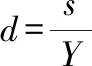
将上翼面的典型归一化目标位移曲线与等截面悬臂梁的归一化位移曲线对比(见图5)可知,两条曲线的变化趋势一致,同一位置处归一化位移近似相等。这说明,在无气动载荷或气动载荷较小情况下,上翼面除S=60%附近的驱动长桁外,无需新增驱动点,即可实现较高精度的变形。
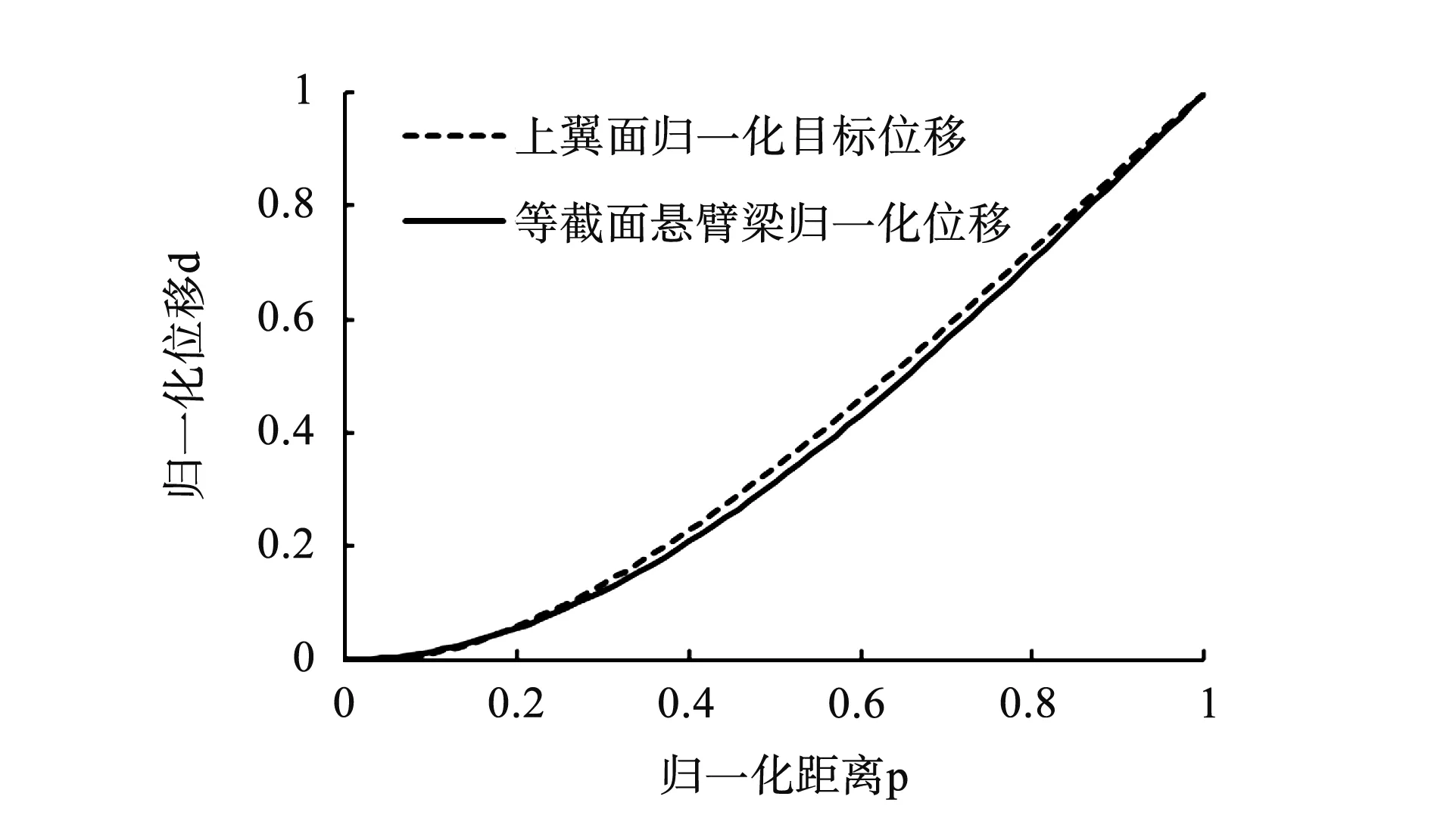
图5 上翼面归一化目标位移曲线与等截面悬臂梁归一化位移曲线对比
同时,由图5的分析可知,即使在上翼面厚度相等时,也能实现较高精度的变形。若要进一步提高变形精度,上翼面各刚度控制区域的蒙皮厚度只需在小范围内调整。
下翼面与上翼面的初始曲率分布状态相似,但其曲率变化幅度明显大于上翼面且存在一个曲率变化拐点A(见图4),因此需在曲率拐点A和S=40%附近各设置一个驱动长桁。
综上所述,下垂状态的精度控制变量主要包括S=0~60%区域内的蒙皮刚度分布、3个驱动长桁的位置及其驱动位移。
2.3 巡航精度控制变量
巡航状态,长桁在内部驱动机构的支撑下和蒙皮共同维持前缘的气动外形,其外形精度的主要控制变量由气动载荷的分布状态决定。图6所示为典型的机翼前缘在巡航状态的气动载荷分布曲线,气动载荷的吸力峰位于上翼面,因此,巡航状态外形精度的主要控制变量为上翼面长桁的位置和蒙皮厚度。
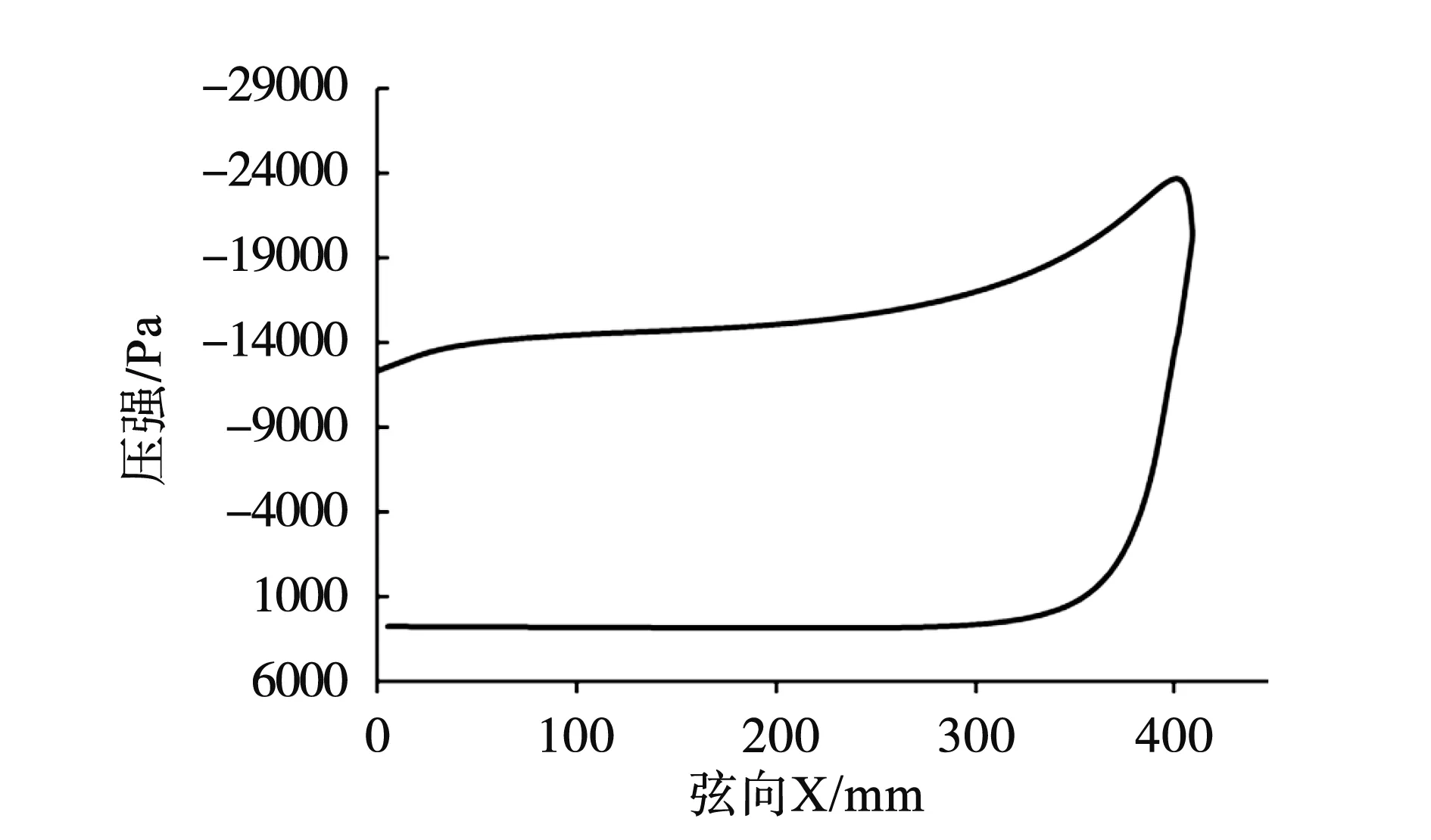
图6 典型的巡航状态气动载荷分布
当前缘弦长较大(大于350mm)时,上翼面若只在S=60%附近设置一个驱动长桁,在吸力峰作用下,上翼面必然会发生鼓起。因此,为维持上翼面的外形精度,需在S=80%附近增加一个长桁。但需要指出的是,该长桁的作用主要是维持巡航状态的气动外形,无需参与下垂状态的结构设计。此外,为尽量减小上翼面的位移偏差,其蒙皮厚度也需较大。
3 数值算例分析
本文的参考模型为某远程公务机的气动验证模型(Aerodynamic Validation Model,AVM),如图7所示。该气动模型的机翼前缘具备光滑连续下垂功能,下垂翼型通过气动优化得到。最大下垂角度为17°,其飞行状态为0.2马赫和8°攻角。收紧时的飞行状态(即巡航状态)为0.85马赫。本文截取距离翼根66%展长的模型1为设计对象,其初始状态(即巡航状态)弦长为430mm,周长为957mm,如图8所示。

图7 参考飞机的气动验证模型

图8 模型1的初始形状和目标形状
分别使用现有方法和本文改进后的方法对模型1的柔性蒙皮结构进行优化设计,并从外形精度和优化效率两方面对设计结果进行对比。刚度控制区域划分方式为沿坐标S均匀划分为10个区域,长桁数量设置为4个。
3.1 优化模型设计
柔性蒙皮优化问题的目标函数为:
(3)
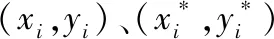
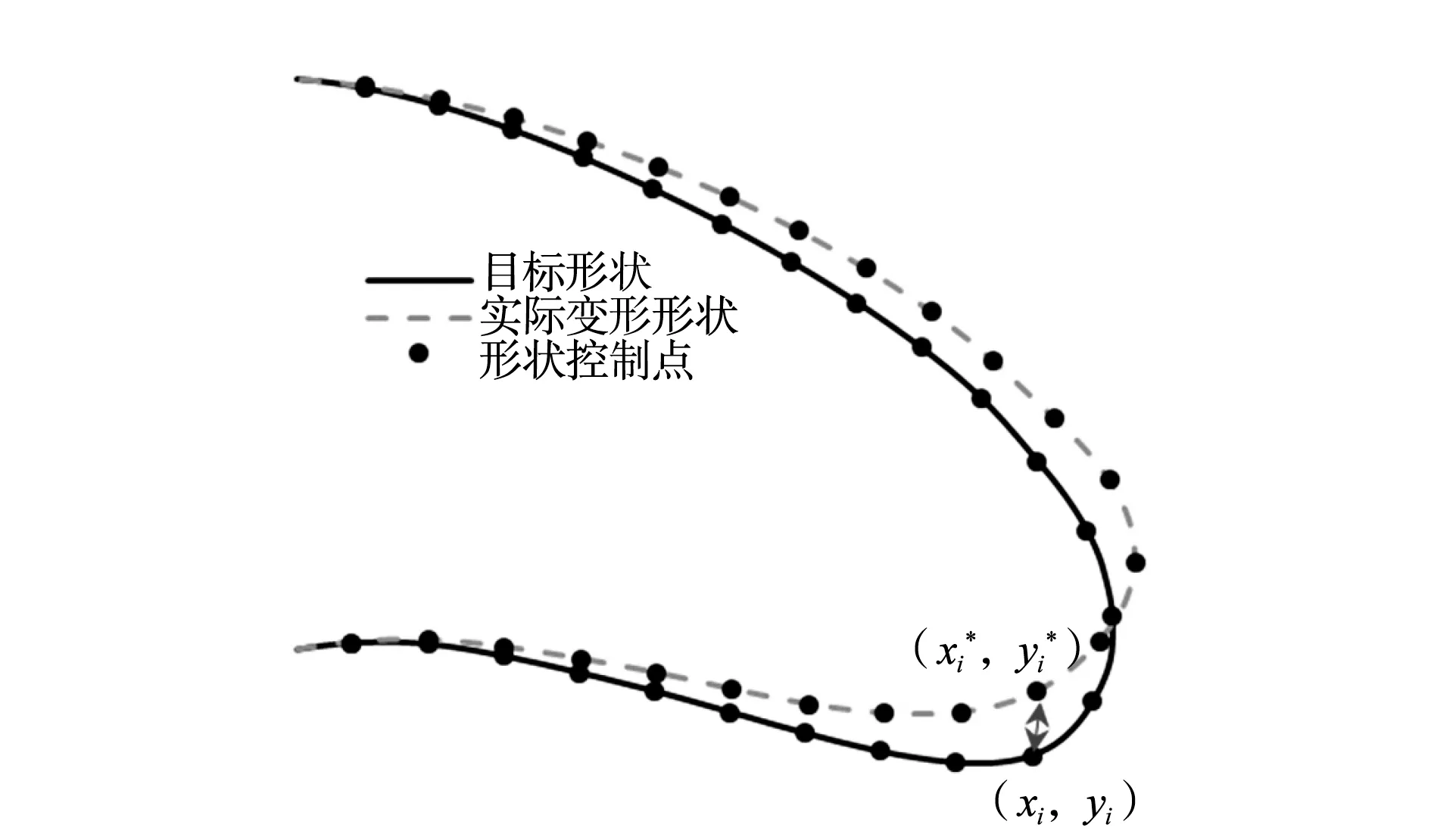
图9 LSE计算方法
模型1的优化变量包括各刚度控制区域的蒙皮厚度、长桁位置及长桁上的驱动位移。其中10个刚度控制区域的蒙皮厚度的约束范围为[1mm,5mm],现有设计方法和本文设计方法优化模型的差别主要体现在长桁和驱动位移的个数及其约束范围。
3.1.1 现有设计方法
现有设计方法中,参与优化过程的长桁个数为4个,其约束范围如图10所示。驱动位移的个数为8个,其约束为:
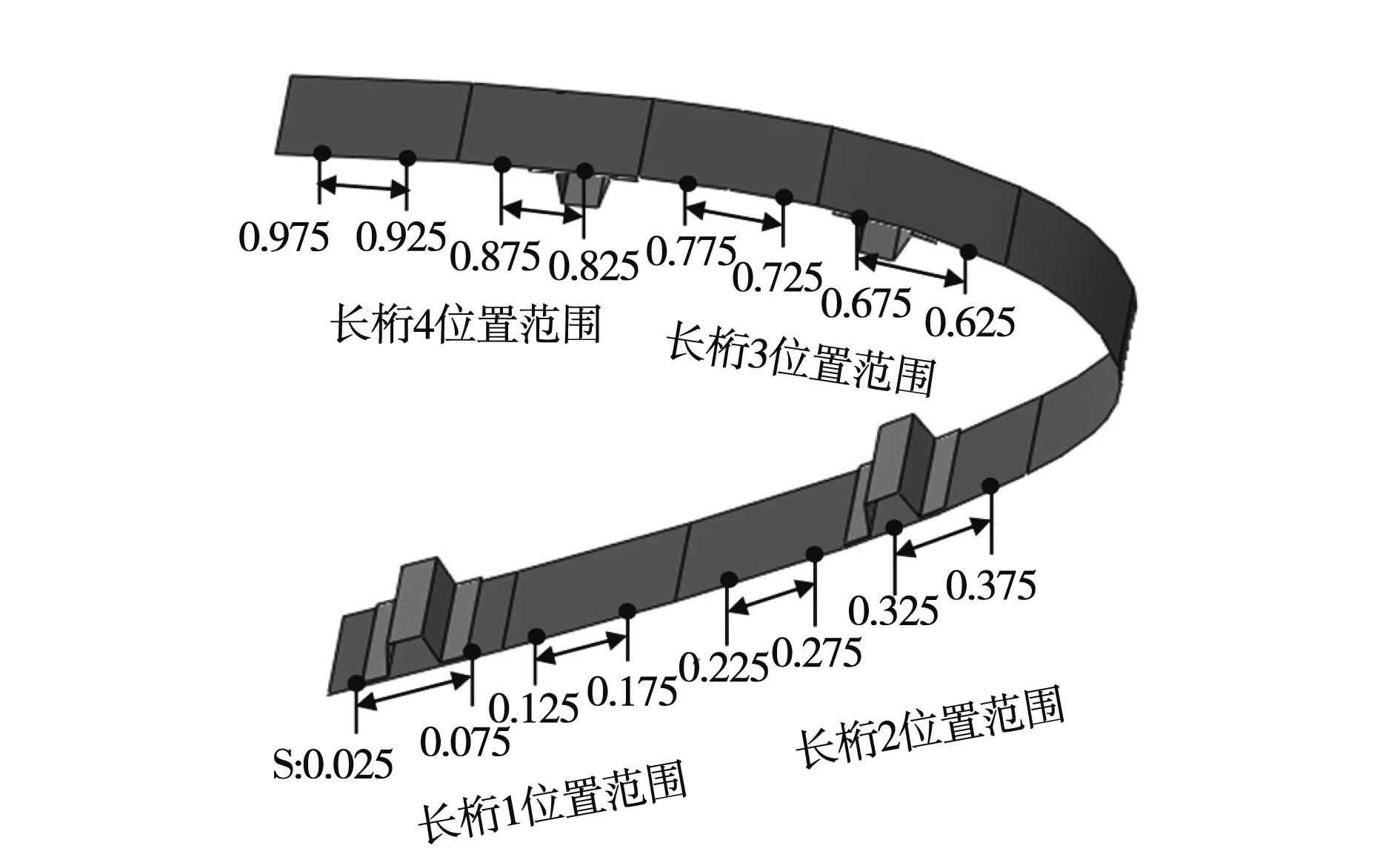
图10 现有设计方法中长桁位置的约束范围
(4)
式中,Six、Siy分别为第i个长桁沿x、y方向的驱动位移,Xi、Yi为第i个长桁定位点沿x、y方向的目标位移。
3.1.2 本文设计方法
本文设计方法中,长桁4固定于S=77.5%,参与优化过程的长桁个数为3个,其中长桁1保持其在现有设计方法中的约束范围,长桁2和长桁3的约束范围分别缩小为S∈[32.5%,37.5%]和S∈[62.5%,67.5%]。驱动位移个数为6个,其约束为:
(5)
式中,Six、Siy分别为第i个长桁沿x、y方向的驱动位移,Xi、Yi为第i个长桁定位点沿x、y方向的目标位移。
综上所述,与现有设计方法相比,本文方法使全局优化变量的个数减少了25%,全局优化变量的约束范围也大幅降低,简化了柔性蒙皮结构的优化数学模型。
3.2 设计结果对比
本文采用带精英策略的非支配排序遗传算法,设置每代个体数量为40个,交叉概率为0.9,变异概率为0.1。现有设计方法经过60代收敛于LSE=0.92mm,本文设计方法经过30代收敛于LSE=0.9mm。
3.2.1 下垂状态的变形精度对比
现有设计方法和本文设计方法的变形结果对比如图11所示。针对整体变形效果,两种设计方法均实现了精确变形,与目标形状吻合度较高,但在对气流分布影响较大的前缘前端,现有设计方法的最大位移偏差为5.3mm,本文设计方法的最大位移偏差为3.0mm。
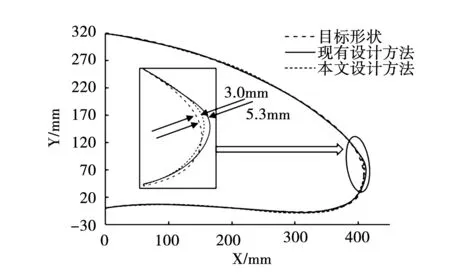
图11 两种设计方法的变形结果对比
图12和图13为目标形状、现有方法和本文方法设计结果的升力系数、升阻比曲线,由曲线对比可知,前缘前端的位移偏差影响了机翼的气流分布,目标形状的升力系数、升阻比明显优于两种设计结果,这说明,针对该变形目标,前缘的变形精度会对机翼的气动效率产生较大影响。在8°攻角时,相较现有方法,本文方法设计结果的升力系数提高了1.3%,升阻比增大了5.7%,气动性能优于现有方法的设计结果。

图12 目标形状、现有方法和本文方法设计结果的升力系数曲线
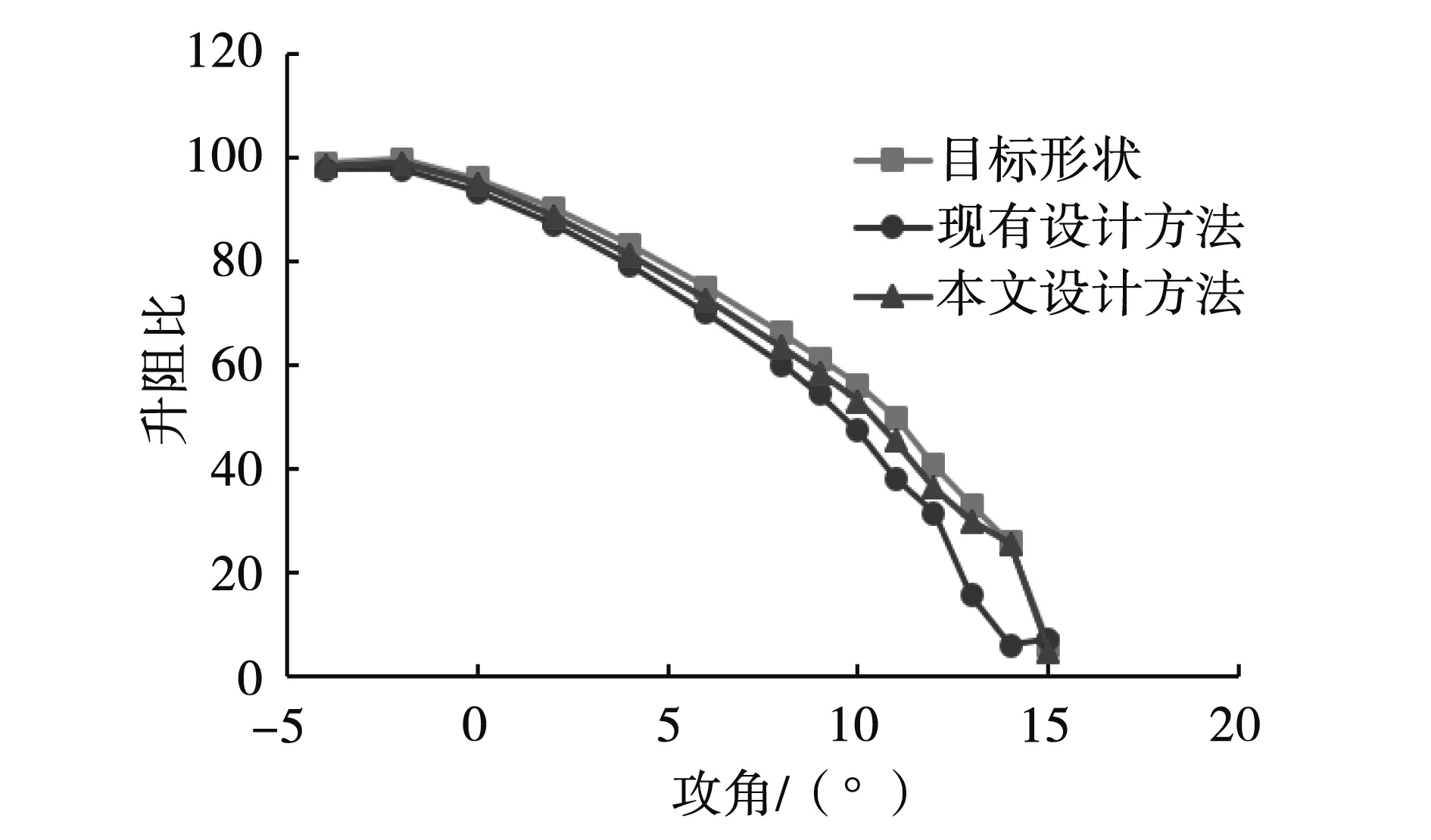
图13 目标形状、现有方法和本文方法设计结果的升阻比曲线
3.2.2 巡航状态的外形精度对比
巡航状态下,现有方法的最大位移偏差为6.0mm,而本文方法为2.7mm,外形精度明显提高(见图14),更符合自然层流翼型的要求。
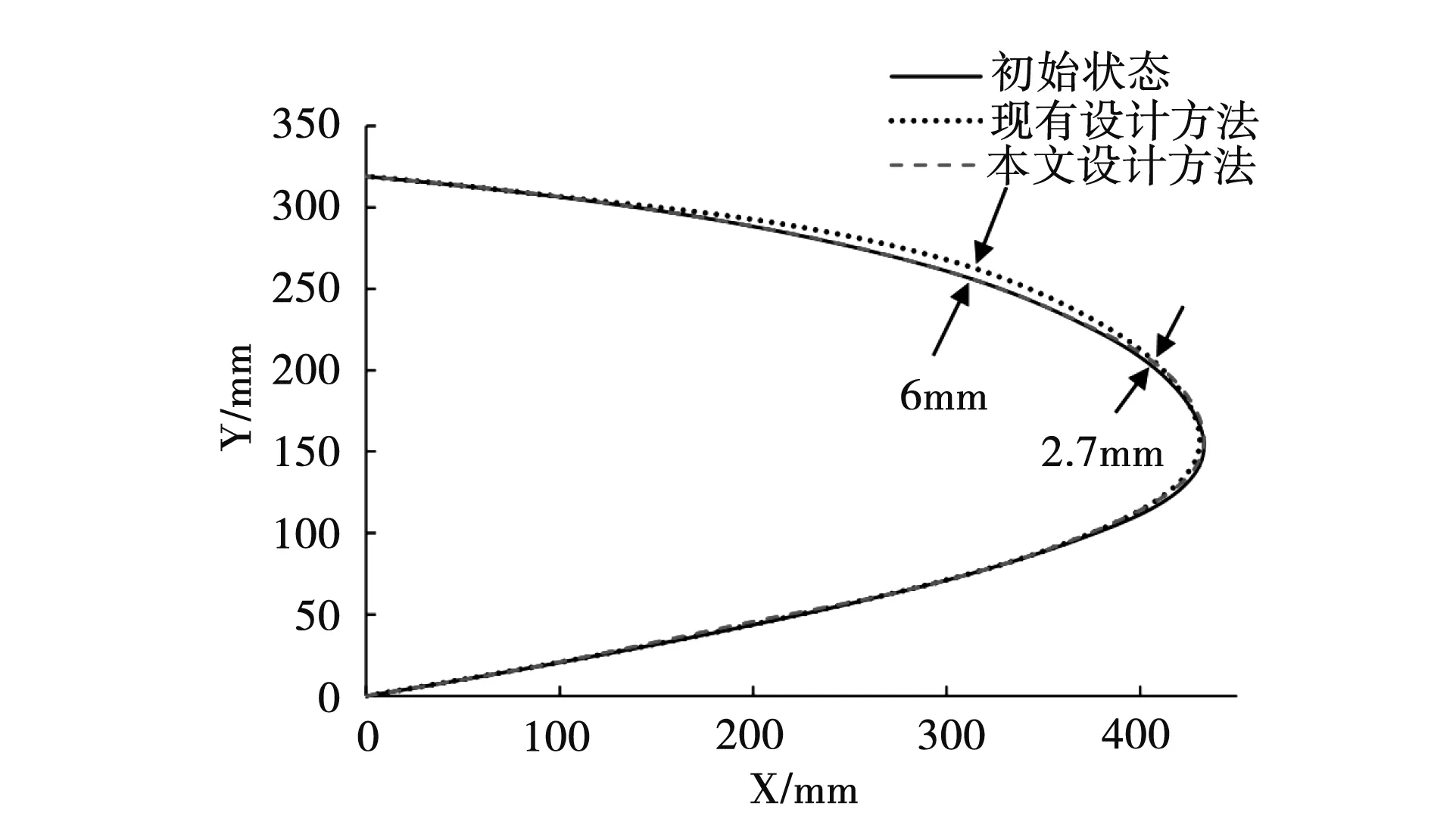
图14 现有方法和本文方法的巡航状态外形形状对比
4 结 论
(1)本文为机翼变弯度前缘柔性蒙皮提供了一种新的优化设计方法,根据变形机理分析将设计变量分为全局和局部变量、下垂精度控制和巡航精度控制变量,并通过对下垂和巡航精度控制变量的分步设计,减小了优化模型中全局变量的数量和约束范围,解决了难以同时实现巡航、下垂状态高精度气动外形的问题。
(2)以大型远程飞机变弯度机翼前缘为对象,应用现有和本文方法进行了柔性蒙皮的优化设计,数值仿真结果表明,本文方法可使下垂状态和巡航状态的最大位移偏差分别降低43%和55%,有效提升机翼的气动效率。
(3)通过对下垂、巡航状态气动外形精度的综合分析可知,巡航状态的高精度外形可通过增加上翼面的长桁个数、蒙皮厚度较容易地实现,而下垂状态的精确变形则需要通过对各类结构变量的优化设计实现。本文方法能够提高柔性蒙皮变形精度的主要原因是对下垂精度控制变量进行了单独优化,减少了优化模型中全局变量的数量。
