基于飞机伺服弹性试验的操纵面旋转模态测试技术

李晓东，杨文岐，宋巧治

(中国飞机强度研究所 二室，陕西 西安 710065)

1 引 言

由于生产超差、装配误差及运动过程中的磨损等因素的累积，飞机操纵面存在摩擦、间隙及传动系统的不确定性等非线性影响，导致操纵面旋转支持刚度下降，影响飞机的颤振特性或出现极限环等气动弹性不稳定现象[1，2]。所以，需要对飞机进行振动特性和气动弹性分析。但是，由于操纵面存在着强烈的非线性影响，采用计算的方法很难获得准确的动力特性，必须经试验验证和修正。因此，获得准确的操纵面旋转频率是非常重要的。

目前，国内外在飞机地面振动试验中，采用渐进变力法消除非线性的影响，进行操纵面旋转模态的测试，当力变化而频率不变时，测得的频率即为操纵面旋转频率[3]。一般情况下，采用这种方法都能够达到很好的效果，但是对间隙摩擦等较大的情况，要达到频率稳定，需要很大的激振力，这可能存在操纵面振幅过大，激振器行程不够的情况。另外，采用激振器加力是在操纵面的一个点上施加集中力，由于结构强度限制，有可能在大力下使操纵面损坏。对于导弹及小型飞机，由于操纵面质量较轻，激振器可能引起附加质量和附加刚度的影响。这些因素都可能影响操纵面旋转模态测试的精度。

飞机伺服弹性地面试验用于测试控制系统与结构之间的动力耦合特性，包括开环频率响应试验和闭环稳定性试验[4-6]。开环频率响应试验是通过飞控系统给操纵面施加一正弦扫频信号，驱动操纵面做正弦运动，测试飞控/机体系统的传递函数。而在进行开环频率响应试验时，同时在操纵面上布置加速度传感器，并在扫频的过程中采集操纵面的响应信号，根据工作模态识别方法进行操纵面旋转模态的识别，就可以获得操纵面的旋转模态，不受激振器的限制，同时也不存在激振器附加质量和附加刚度的影响，施加的激振力也不是一个集中力，避免了大力下对操纵面局部的损伤。

本文介绍了基于飞机伺服弹性地面试验获得操纵面旋转频率的测试方法，并以一飞机为对象进行了应用验证。试验结果表明，这种方法是可行的，具有一定的工程应用价值。

2 基于飞机伺服弹性试验的操纵面旋转模态测试原理

2.1 试验原理

基于飞机伺服弹性试验的操纵面旋转模态测试是在开环频率响应试验的基础上进行的，断开飞控系统中增稳舵机和控制增稳计算机的连接线，由外接信号发生器给增稳舵机输入正弦扫频信号，此时操纵面就做正弦运动，测量控制增稳计算机输出端的速率陀螺输出，同时测量操纵面上加速度响应。采用工作模态的识别方法进行模态识别和分离，具体原理见图1。由于在开环频率响应试验中也要求克服操纵面的非线性影响，幅值大小的确定应能够克服操纵面的非线性影响。

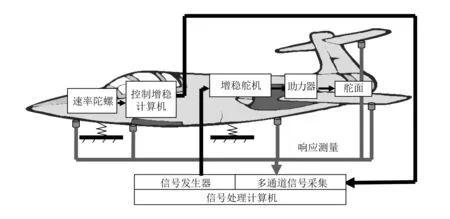
图1 试验原理图

2.2 基于操纵面响应数据的模态参数识别

传统的模态参数识别是建立在系统的输入输出都已知的基础上的，在外界激励未知的情况下，仅拾取实际工作状态下的结构响应来进行结构的模态参数识别，即为工作模态分析OMA[7，8]。原理如下：

一个n自由度系统在白噪声激励下，结构上i、j两点响应的互相关函数可表示为：

(1)

式中：Gjr为仅同测量点j和模态阶数r有关的常数项；

θr为同模态阶数r有关的相位角。

同时，脉冲响应函数xij(t)可表示为：

(2)

将互相关函数Rij(T)的这一表达形式同脉冲响应函数xij(t)比较，可以看出，二者形式相同，都能表示成衰减正弦函数的和，即每个衰减正弦都有一个自然频率和阻尼比同结构的各阶模态相对应，不同的只是常数项和相位角。因此，可以将结构两点间响应的互相关函数Rij(T)代替脉冲响应函数xij(t)，采用那些原本需要利用脉冲响应函数的时域模态参数分析方法进行未知激励下的模态参数识别，或者对结构两点间响应的互相关函数Rij(T)进行傅里叶变换，得到结构两点间响应互功率谱，替代频响函数。

采用工作模态识别模态参数的过程先对响应信号进行采样,在进行多个测点的模态参数识别过程中，需要选取一个测量点作为参考点，一般选取响应较小的测点作为参考点，计算其它测点与该参考点的互相关函数(或者互功率谱)，将计算的互相关函数作为脉冲响应函数(频率响应函数),利用传统的时域(频域)模态识别方法进行工作模态参数识别[9，10]。

3 应用验证

本次应用验证是在某型飞机上进行的。在飞机上进行伺服弹性地面试验时，给飞机的每个操纵面上布置4个加速度传感器，机身和翼面上各布置2个加速度传感器。根据开环频率响应试验原理，将控制增稳计算机和增稳舵机断开，然后给增稳舵机俯仰回路施加一正弦扫频信号，驱动升降舵做正弦运动。力的幅值通过试验确定，确保能够克服间隙等非线性的影响，通过采集器采集到升降舵上的响应信号的时间历程，时间历程曲线如图2所示。通过对时域数据的观察，选取机身上的响应信号作为参考点，与采集到的升降舵上加速度时域数据进行互功率谱函数的计算，图3为互功率谱曲线。

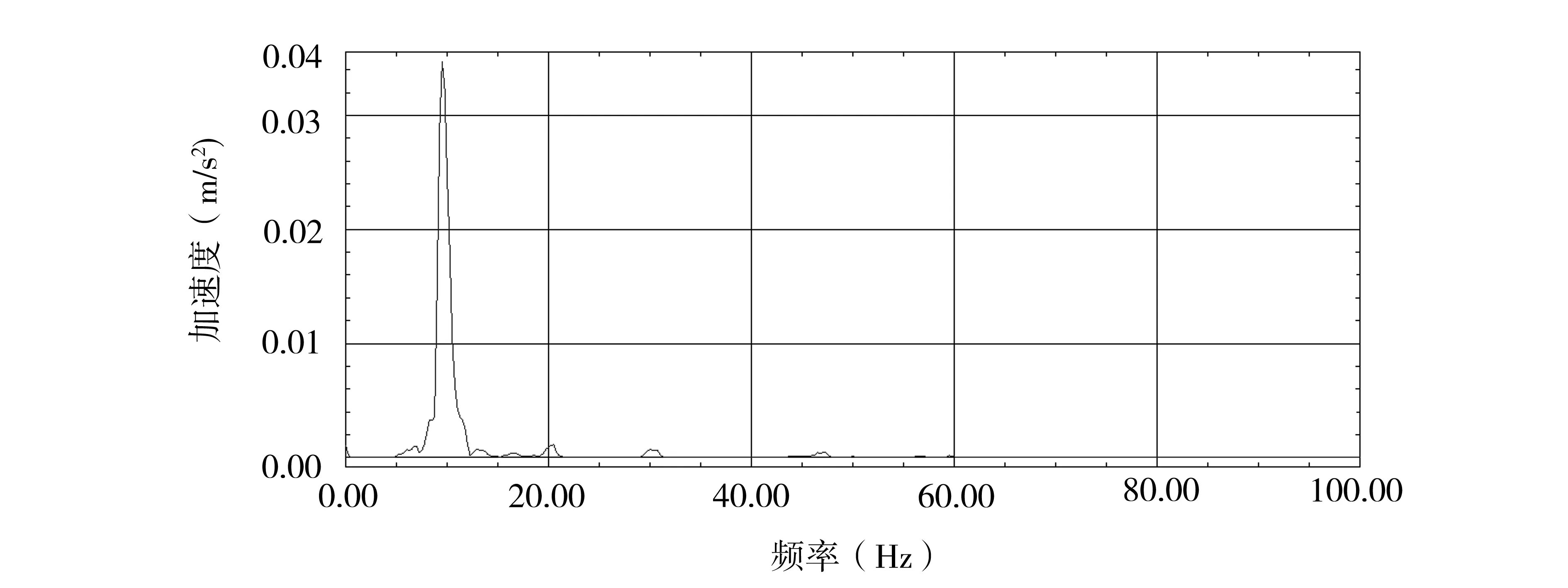
图3 互功率谱曲线

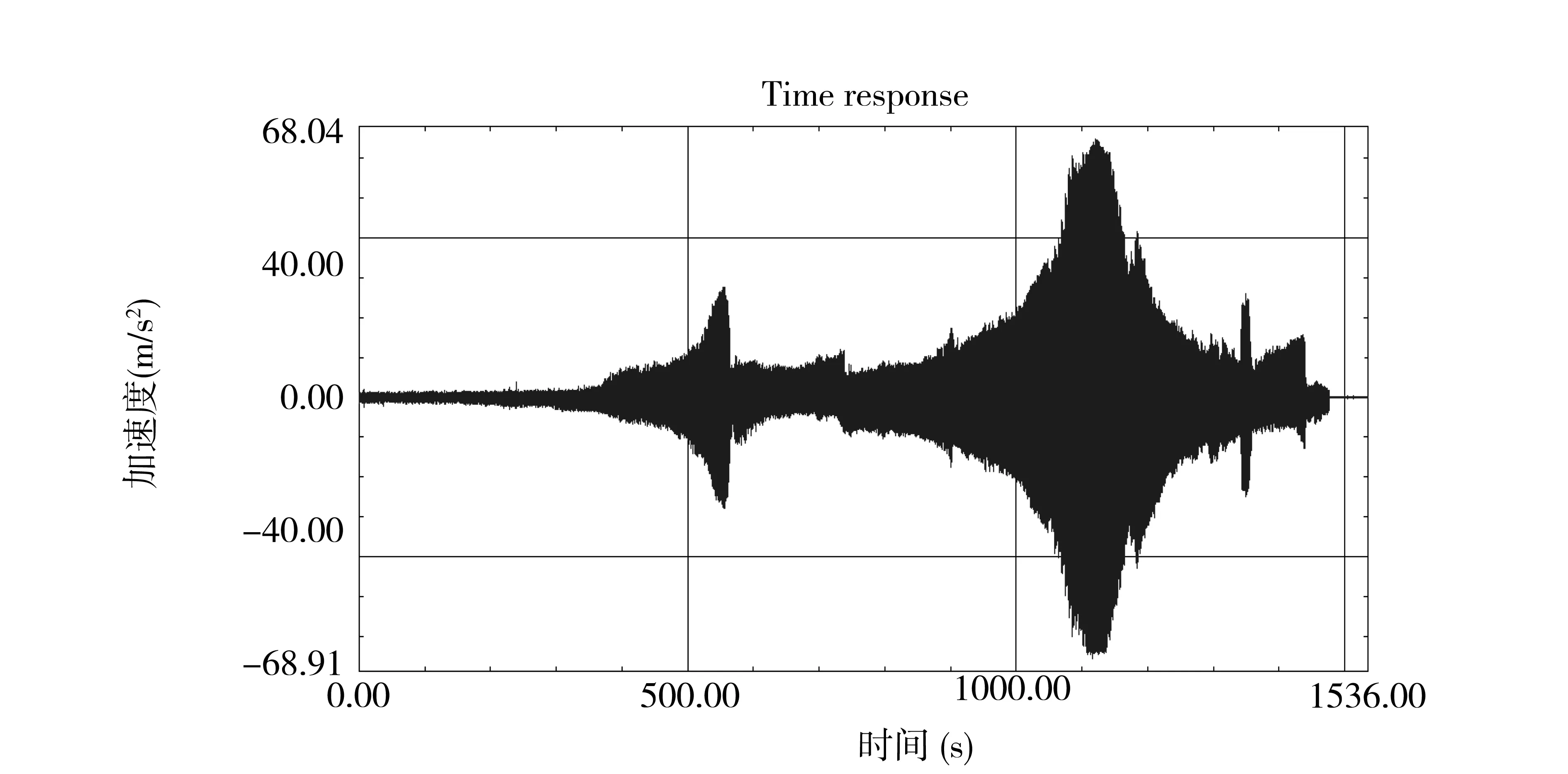
图2 升降舵上的时间响应历程

利用得到的互功率谱函数作为频响函数，利用传统的基于频响函数的模态参数识别方法进行基于响应信号的工作模态参数识别。最终得到左升降舵的旋转模态频率为9.5Hz，右升降舵的旋转模态频率为9.75Hz。在地面振动试验中，通过变力得到的左升降舵旋转频率为9.91Hz，右升降舵旋转频率为10.02Hz。从两种方法得到的结果看，误差还是较小的。

4 结束语

基于伺服弹性地面试验获得的操纵面旋转模态和地面振动试验中通过变力得到的操纵面旋转频率误差较小，地面振动试验得到的旋转频率偏大，可能是由于激振器的附加刚度造成的。试验结果表明，该方法是合理可行的，对操纵面小且轻的导弹尤其适用，可以减少激振器附加刚度和附加质量的影响，避免力过大引起的操纵面损坏，对于提高操纵面旋转频率的测试精度具有一定的工程意义。