基于修正邓肯-张模型模拟红黏土应力-应变关系

2020-08-18谷建晓范理云吕海波1陈宜虎

桂林理工大学学报 2020年2期

谷建晓,范理云,吕海波1,,陈宜虎

(1.桂林理工大学广西岩土力学与工程重点实验室, 广西桂林 541004; 2.Department of Civil, Architectural and Environmental Engineering, Missouri University of Science and Technology, Rolla, MO 65401, USA; 3.贺州学院建筑工程学院, 广西贺州 542899)

0 引言

天然土有结构性,对土的力学性质具有重要影响,沈珠江院士把土结构性模型的建立称为“21 世纪土力学的核心问题”[1], 谢定义等也认为“土结构性是决定各类土力学特性的一个最为根本的内在因素”[2]。众多研究者以土结构性变化参数与物理力学参数间关系建立模型,以此发展出结构性剑桥模型[3-4]、考虑结构性的模型[5-6]、结构性双硬化模型[7-9]、考虑扰动的结构性模型[10-11]等。其中,以损伤理论建立的结构性模型,由于其概念清晰、原理易懂、参数可求等优点被广泛使用。以沈珠江等提出的土体损伤理论[12]为起点,学者们以损伤规律为基础建立结构性模型。这些弹塑性模型被应用到砂土、堆石料、不同土体界面等研究中[13-19],取得了一定的成果,但其模型计算较为复杂,难以广泛应用;而邓肯-张模型是典型的非线性弹性模型,可描述应力-应变硬化曲线而被广泛用于预测和计算应力-应变曲线[20-23]。为描述结构性土的应力-应变曲线,王立忠等[24]提出了考虑结构性修正的邓肯-张模型,将结构性损伤进行分段描述,使其能应用于结构性土,但其损伤参数要通过多次的试算,计算过程稍显复杂。

红黏土是一种特殊性土,主要分布于云贵高原及其毗邻的广西中、西部,因具有反剖面特征,使其上硬下软,在地基基础、水利、公路、边坡等工程应用中因结构性导致众多工程问题，其结构性来源于红土化作用,即湿热多雨、干湿循环作用,使难溶氧化物不断聚集、胶化、陈化,联结松散颗粒形成整体,具有显著的结构性。因此，有必要首先分析现有的试验数据,从结构性损伤角度进行分段描述,分析其应力-应变曲线特征。

本文在修正邓肯-张模型的基础上,提出一种方法计算损伤比,得到相应的损伤速度,分析损伤速度与结构性的关系,简化损伤参数的求解,确定红黏土主要的结构性损伤参数取值范围,以深化对红黏土结构性的认识。通过对比模拟数据与试验数据,模型较好地描述应力-应变特征,对工程设计施工具有一定借鉴意义。

1 应力-应变特征分析

红黏土具有高含水量、高塑性、高孔隙比、低密度、压实性差等特点, 其结构性因土中含水量、颗粒大小、排列方式、孔隙的组成与分布,以及颗粒间接触和联结作用的不同,对其力学性质产生很大影响，其结构性表现为:在小应变时,应力-应变曲线陡峭,对应的应力增幅较大;在大应变时,应力-应变曲线较为平缓,应力增长较小,如图1所示。

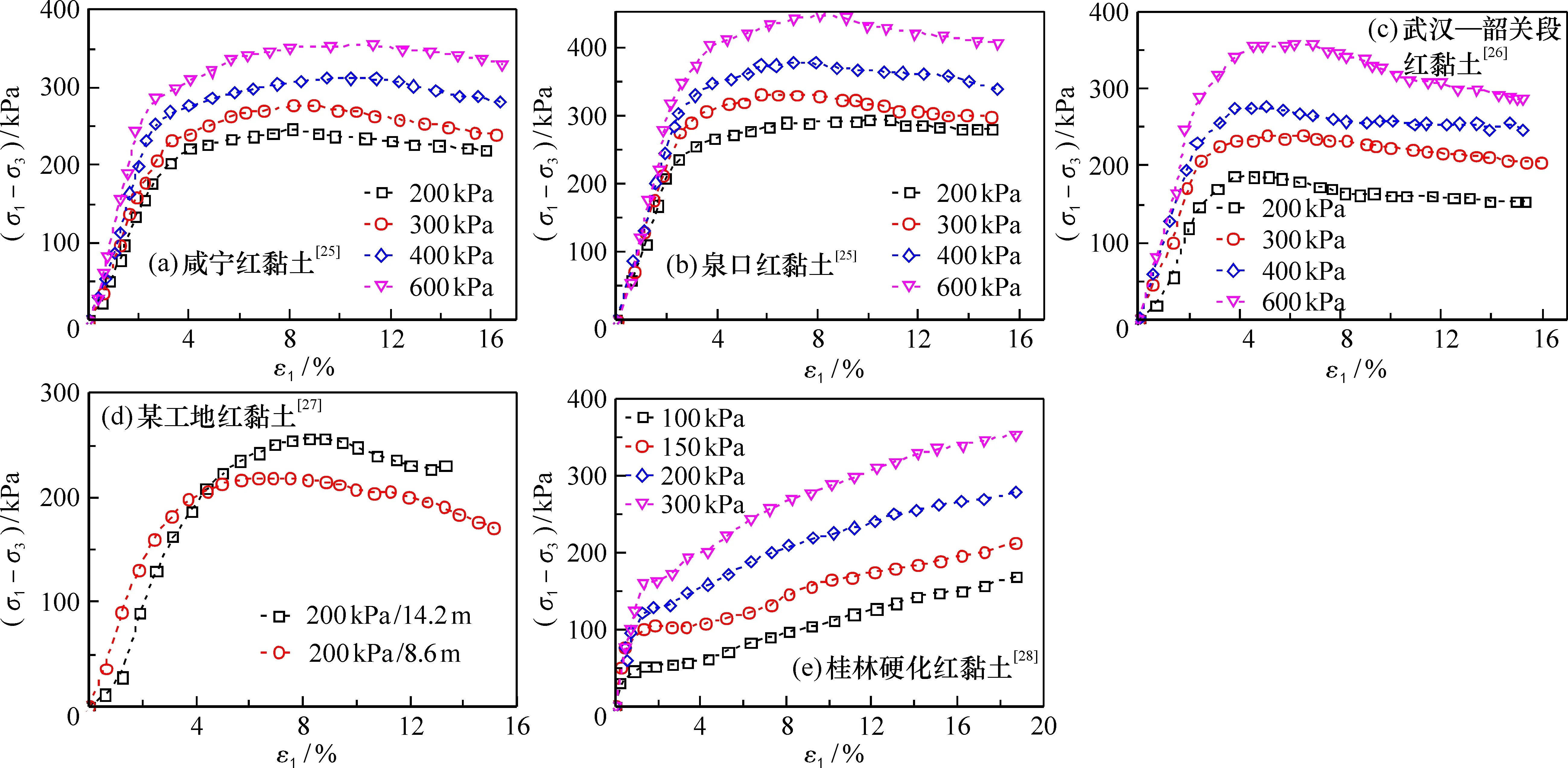
图1 不同地区红黏土三轴固结不排水试验的应力-应变曲线Fig.1 Stress-strain curves of triaxial consolidation undrained test of red clay in different areas

按红黏土的应力-应变曲线特征可分为硬化(咸宁、桂林)和软化(泉口—围压300 kPa和武汉—韶关段)两种类型，如咸宁红黏土随围压的升高, 其应力-应变的硬化现象越来越明显。硬化现象可解释为: 由于试样的密度在整个剪切过程中基本保持不变, 在试样未被压密前, 孔隙压力随有效应力增加而增加；当被压密实后, 孔隙压力减低甚至负孔隙压力, 有效应力持续增加,表现出应力-应变硬化。通过上述试验应力-应变曲线关系的分析可知, 红黏土的应力-应变曲线可归纳为S型曲线。

结合红黏土的变形特征和相关文献资料, 将其划分为4个阶段: 挤密阶段、弹性阶段、破损阶段、破坏阶段(图2)。已有的相关黏土研究成果也发现有类似的规律, 因而此分段具有一定可信度。对图1中原状红黏土三轴试验数据分析, 可将前两阶段定义为结构强度变形的第1阶段; 而破损阶段定义为结构强度变形的第2阶段; 将破坏阶段定义为结构强度变形的第3阶段, 此时应力-应变曲线将会有3种不同的发展趋势: 曲线上扬(硬化)、曲线下拐(软化)和水平发展(蠕变)。

图2 红黏土偏应力-应变关系特征Fig.2 Characteristics of relation between deviatoric stress and axial strain for red clay

2 修正模型建立

2.1 邓肯-张模型

在以σ3为常数的常规三轴试验中,土样的应力-应变关系可近似描述为如图3所示的双曲线函数[29]

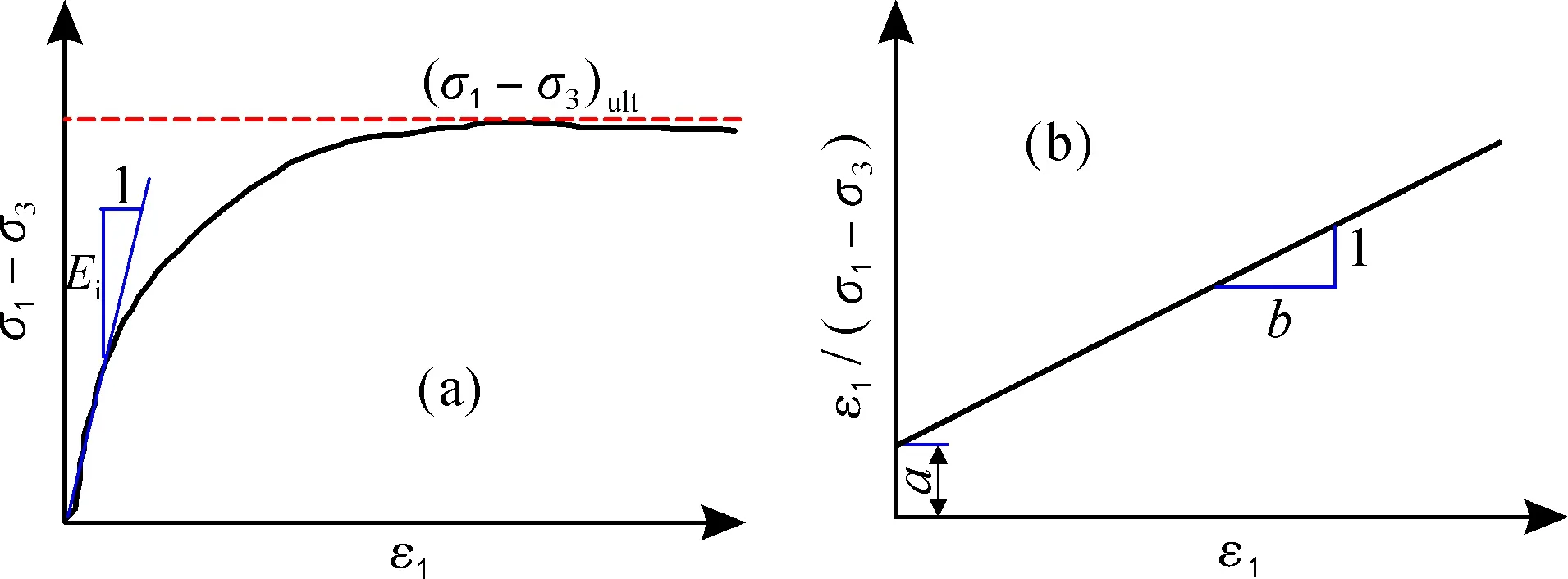
图3 应变硬化型红黏土应力-应变关系曲线[24]Fig.3 Stress-strain relation curves of strain hardening red clay

(1)

2.2 考虑结构性的邓肯-张模型

沈珠江推广了结构损伤规律[12,15,17],并在1993年给出了损伤比的计算公式，将过渡段的结构土体看作无损原状土和重塑土的结合体，施加荷载,其变化过程可表示为

S=(1-ω)Si+ωSd,

(2)

式中:S为过渡段结构土体力学参数;Si为原状土体的强度力学参数;Sd为损伤土(扰动土)的强度力学参数(与Si为同一力学参数);ω为损伤比, 即损伤部分占整个土体的比例。

王立忠等[24]引用沈珠江损伤概念, 对邓肯-张模型进行修正, 使其适宜于描述结构性黏土的应力-应变特征。对于常规三轴试验(固结压力小于结构屈服应力时),应力-应变软化型和硬化型的关系曲线ε1/(σ1-σ3)-ε1分别可用3段和2段直线拟合(图4), 拟合直线的截距为初始切线模量的倒数。改进的双曲线函数较好地模拟了应力-应变关系, 本文仍采用改进的双曲线函数

图4 结构性红黏土切线模量拟合Fig.4 Fitting curves of tangent modulus for structured red clay

(3)

2.3 损伤比修正

考虑结构性的邓肯-张模型的损伤比ω是通过与破坏应变有关的公式计算得出的,其中损伤比ω、损伤参数a*的取值是通过不断反算得出最优解(结构性黏土为15),没有给出具体的计算方法。为克服此问题,现提供一种计算损伤比的方法,再通过拟合损伤比与应变的关系曲线得出数学表达式。

在某一围压下, 试样的应力-应变曲线可分为3个阶段：对于第3段,土体近乎重塑土, 损伤比ω=1, 则不用求解a*值，损伤速度与土体结构强度有关, 损伤速度在整个过程中不断增大, 并伴随土体结构破坏, 尤其在第3阶段达到最大值; 但对于第1阶段(弹性和挤密)和第2阶段(破损)都存在较为完整的结构强度, 损伤速度变化较小, 因此假设前两阶段的损伤速度为定值, 方便进行损伤速度的求解。损伤比求解可借助其概念求得

(4)

式中:Ei(ε1)为轴向应变对应的切线模量;Ei1为第1阶段的切线模量;Ei2为第2阶段的切线模量。当Ei(ε1)>Ei2时, 表明应力-应变曲线关系进入第3阶段, 土体近似重塑试样,ω=1。

通过观察图3a和式(1)发现，Ei(ε1)是一个关于应变的函数

(5)

式中:a、b为对应的应力-应变曲线段的参数值, 可将数据绘制在ε1/(σ1-σ3)-ε1坐标系图3b中求出。

损伤比是关于最大轴向应变的函数, 只有一个未知数, 因此求得文献试验数据的损伤比与应变的关系如图5所示, 发现此关系呈现一定的函数关系, 借鉴文献[30]损伤比的表达式，且考虑轴向应变, 通过MATLAB数值拟合得到：

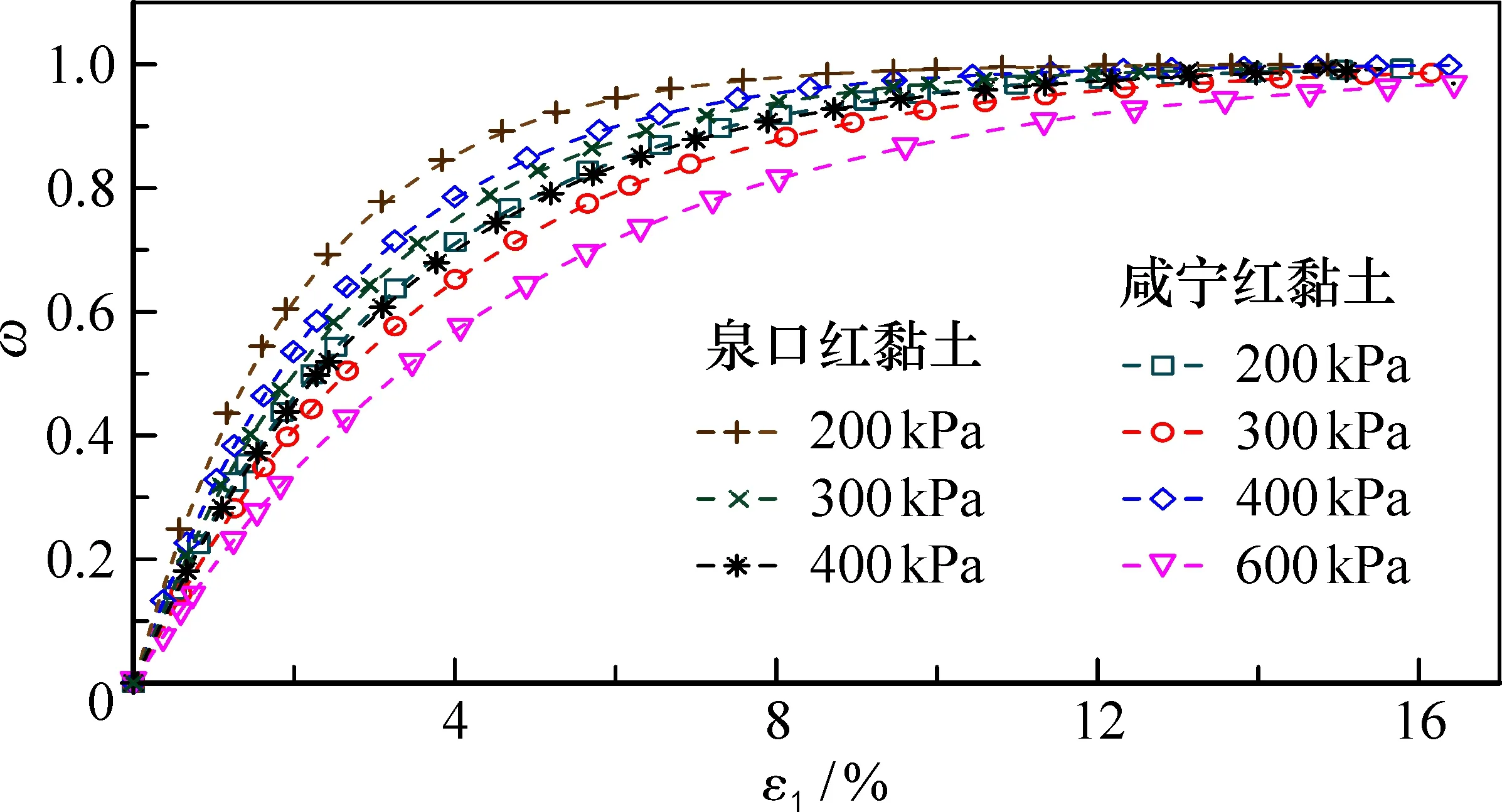
图5 结构性红黏土损伤比与应变关系Fig.5 Relation between damage ratio and strain of structured red clay

ω=1-e-a*ε1,

(6)

其中，损伤参数a*表示土体的结构性在应力作用下的损伤速度。对于原状土体,其压实挤密所造成的变形过于微小,可将弹性和破损阶段用修正后的模型模拟；而对于破坏阶段,土体近乎重塑土,仍用邓肯-张模型模拟其应力-应变曲线关系,其破坏的判定是应变达到15%～20%。

3 修正模型求解

3.1 参数求解

对于式(3)双曲线函数模拟应力-应变曲线只需要确定5个参数即可, 即Ei1、Ei2、 (σ1-σ3)ult1、(σ1-σ3)ult2和a*参数, 以上参数可通过三轴试验得出。以其中一个试验数据求解作为示例:剔除试验数据起始异常跳跃点, 按ε1/(σ1-σ3)-ε1为坐标系处理三轴试验数据。土体的屈服应力状态会随着荷载条件变化而不同, 对于常规三轴压缩试验, 因球应力会对土体产生结构损伤, 当足够大时, 就会出现明显的损伤, 会在应力-应变曲线上出现明显的拐点, 将此时的主应力差看作结构屈服应力, 将此点作为第2和第3阶段的分界点。当试样发生明显的损伤时, 其切线模量会发生大的变化, 在图6坐标系中表现为截距的变化,曲线曲率最大点意味着前后两段曲线的截距发生了较大变化,也就是说切线模量发生了较大变化。

图6 武汉—韶关段红黏土应力-应变曲线Fig.6 Stress-strain curve of Wuhan-Shaoguan red clay

将试验数据按ε1/(σ1-σ3)-ε1为坐标系处理, 对于应力-应变硬化型红黏土, 只存在前两个阶段,通过数据处理软件分析曲率最大的点作为转折点, 如图6中A点(方框)，且两个连续线段拟合, 要求拟合度都达到0.95以上, 按照公式求解参数Ei1、Ei2、 (σ1-σ3)ult1、(σ1-σ3)ult2，可得Ei1为b的倒数、 (σ1-σ3)ult1为a的倒数, 以此类推可求出Ei2、 (σ1-σ3)ult2。各计算参数见表1。

表1 武汉—韶关红黏土应力-应变计算参数Table 1 Stress-strain calculation parameters of Wuhan-Shaoguan red clay

对图1中的原状红黏土三轴试验数据分析,可将前两阶段视为结构强度变形的第1阶段;而后将破损阶段定义为结构强度变形的第2阶段;最后把破坏阶段看作结构强度的第3阶段。

对于应力-应变软化型, 前两阶段的参数确定与硬化型一样, 第3阶段用邓肯-张模型, 这是因为第3阶段结构强度已完全破坏, 接近于重塑土, 而邓肯-张的双曲线函数可较好地描述重塑土的应力-应变关系, 相关参数按照原模型参数求解方法求解。

根据Janbu的经验公式确定切线模量(Ei1,Ei2)与σ3的关系

Eij=kpa(σ3/pa)n,

(7)

式中:Eij为切线模量(j=1,2);k为卸载回弹模量系数;n为拟合幂次，可通过不同围压下的试验数据拟合得到k、n值;pa为标准大气压(101.33 kPa)。

(σ1-σ3)ulti=k1pa(σ3/pa)n1,

(8)

式中: (σ1-σ3)ulti为偏应力极限值(i=1,2);k1为拟合系数;n1为拟合幂次，可通过不同围压下的试验数据拟合得到k1、n1值;pa为标准大气压(101.33 kPa),各计算参数见表2。

表2 武汉—韶关红黏土应力-应变参数归一化Table 2 Normalization of stress-strain parameters of Wuhan Shaoguan red clay

3.2 参数意义

在土体变形第1阶段(弹性和挤密)的初始切线模量较大, 变形较小; 第2阶段(破损阶段)产生了大量的破损, 且速率加快, 切线模量比第1阶段的要小, 即在相同荷载增量作用下变形较大; 第3阶段(破坏阶段)时, 结构完全破损, 轴向应力随着应变的增大而逐渐减小, 其切线模量甚至可能出现负值。(σ1-σ3)ult1表示在类弹性变形范围内可达到的主应力差极限值， (σ1-σ3)ult2表示土体在破坏前所能达到的主应力差极限值,与邓肯-张模型中的含义相同。

结构性强度是土的固体颗粒的特定排列及其相互, 由于孔隙水中析出的沉淀物(如碳酸盐、游离铁、铝氧化物等) 引起的胶结作用等因素产生的附加强度,通常用抗压、抗剪、抗拉等数值反映(原状土与相应的重塑土间的强度差值),如湛江灰色黏土无侧限抗压强度,原状样6.2 kPa,重塑样0.65 kPa,其差值就是结构强度[31]。此时参数a*也有类似的表示意义,结构性强度越大,损失速度就相对越小。当土体结构性为0,损伤比为1,接近于重塑土,损伤速度a*表示结构性强度的损失快慢,现假定不同的损伤速度参数,用式(4)试算损伤比,结果如图7所示。随着损伤速度的增大,曲线上凸的程度越来越明显,即试样在小应变时,结构强度的损失越大,越接近于重塑土的性质。

图7 不同损伤参数a*模型损伤比-应变对比Fig.7 Comparison of model damage ratio-strain under different damage parameter a*

如图8所示, 随着围压的增大,a*值也随之减小, 呈现一定的数学关系:a*代表的是在外力作用下土体结构的损伤速度, 高围压下固结的土的结构性前期损伤较大, 因此其后续破坏过程中损伤发展相对缓慢,a*值也减小, 土体中结构性强度在对抗外力作用中的作用越来越小。

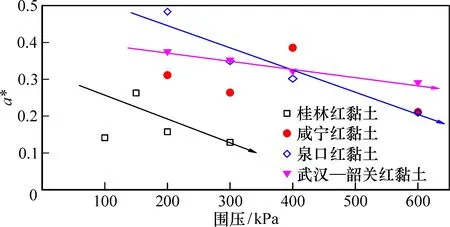
图8 各地红黏土损伤速度与围压关系Fig.8 Relation between damage velocity and confining pressure of red clay in different areas

同一种土的a*值随围压增加而整体呈现减小的趋势。另外,对比不同地区的红黏土发现,应力-应变呈硬化型的桂林红黏土的a*值较低,而软化型的泉口、武汉—韶关段红黏土则较高,表明软化型红黏土结构性相对较强。随着围压的增大,a*取值在0.15～0.35,可作为参考区间,有且仅适用于本文所研究的结构性红黏土,由于试验数据有限,取值范围仅供其他地区红黏土参考。

4 模拟结果分析

将本文与文献[24]两种模型的模拟结果绘制于同一坐标轴中对比。如图9所示,对于应力-应变软化型的红黏土,本文模型与王立忠的修正模型的曲线几乎重合,较好地模拟了实测数据,但在小应变时,模拟结果均大于实测数据,且拟合偏差较大。

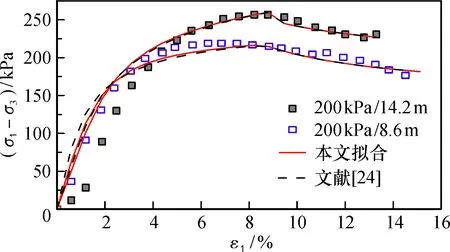
图9 不同模型应力-应变曲线对比Fig.9 Comparison of stress-strain curves of different models

本文模型与原模型比较具有以下优势:新方法通过计算损伤比来得出参数a*的大小, 其变化规律符合实际情况,与原模型的参数获得方法相比更具说服力、意义更为明确。

为了进一步验证本文修正邓肯-张模型对结构性红黏土的适用性,分别进行多组原状土样试验数据的模拟。硬化型曲线用第1和第2阶段就可描述，软化型曲线则具有完整的结构强度变化,其模拟采用修正模型(第1和第2阶段)和原模型(第3阶段)的组合。

模拟结果如图10所示, 在小应变时(约<2%), 模拟结果大多数要高于试验曲线,与现实的情况符合。因红黏土属于裂隙性土, 裂隙压密在极小的应力下就可以实现(轴向应变0 ～2%)[30]。裂隙压密后, 土体强度由结构强度起主要作用, 呈现弹性变形性质的直线段; 当围压进一步增大, 土体进入下一阶段, 发生微破裂, 产生更大应变, 即在相同应力下, 模拟结果的应变小, 模拟的曲线形状与试验数据曲线形状类似。在大应变下, 两者的拟合度较高,但是模拟曲线在第2和第3阶段交界点即开始软化点处与试验数据有出入(图10c)。这主要是因为此点是修正模型和原模型的交界点,两模型参数的求解方法不同,造成此处曲线的突兀：邓肯-张模型采用切线模量是剩下曲线段应力水平50%和95%, 且土体已经进入到了第3阶段, 切线模量较之前小,甚至为负; 而修正模型计算所用的是第1和第2阶段按损伤比折合计算得出; 此外, 还有一种情况会导致小应变部分曲线模拟结果与试验数据吻合度不够, 即在三轴试验中的操作问题导致处理数据时的误差, 小应变数据在ε1/(σ1-σ3)-ε1坐标轴中数据呈现蜿蜒状线型, 而求得的参数是通过拟合实现。