基于PSO- RBF 神经网络的电动汽车锂电池SOC 估算研究与应用
2020-08-18孙文明
孙文明
(浙江农业商贸职业学院,浙江 绍兴 312088)
电动汽车作为应用锂电池最为广泛的对象,利用BMS 对锂电池进行管理,并尽可能发掘锂电池的使用潜能,以延长电动汽车续驶里程,为驾乘人员提供良好的驾驶体验。锂电池SOC 估算作为BMS的核心技术之一,准确对其进行估算,可以保证电动汽车安全可靠行驶,并为电动汽车全面管理提供相应依据。然而,由于锂电池车载工作环境复杂(外界温度在-30~45℃范围、行驶工况为全工况等),且锂电池还具有特征耦合、非线性等特征,导致其SOC 准确估算难度极大[1]。
1 SOC 定义及常用估算方法
1.1 SOC 定义
各国知名车企对SOC 均有自己的理解,但美国先进电池联合会给出的定义被广泛采纳,即:电池在一定放电倍率下,剩余电量与相同条件下额定容量的比值[2-3]。其计算公式为:

式中,Qc为电池剩余的容量,Ci为额定容量。式(1)分子与分母均以电量形式存在,其物理单位为库伦(C)或安时(Ah),1Ah=3600C。SOC 取值范围为0~100%。电池完全充满电时,SOC=100%;完全放电时,SOC=0%。
1.2 SOC 估算影响因素
影响锂电池SOC 估算的因素主要有[3]:
(1)不可逆因素:因制造工艺、长期使用或未定期对电池进行日常维护,出现锂电池发生老化或电极腐蚀等现象。
(2)可逆因素:锂电池受外界影响而发生实时变化的因素,如外界温度、电池内阻(欧姆内阻与极化内阻)、电池循环次数、电池充放电倍率(电流)与电池自放电等。
为了准确估算锂电池的SOC,需要综合考虑各项因素。
1.3 SOC 估算常用方法
常见的锂电池SOC 估算方法如图1 所示[1];估算方法优缺点如表1 所示。

图1 常见的SOC 估算方法

表1 SOC 估算方法对比
因锂电池SOC 与其影响因素存在非线性关系,导致建模困难,而RBF 神经网络可以较好的解决此类问题,因此本文采取RBF 神经网络对电池SOC进行估算的方法,为提高估算结果准确性,将PSO算法引入到RBF 神经网络中,对网络结构隐层节点中心、宽度及连接权值优化处理,从而降低RBF 神经网络参数取值繁杂度。
2 RBF 神经网络与PSO 优化算法
2.1 RBF 神经网络结构分析
RBF 神经网络作为一种具有输入层(取值范围1~n)、隐层(取值范围 1~h)和输出层(取值范围 1~L)三层结构的前向网络神经模型(如图2 所示),其作用是将输入到隐层的非线性可分转变为隐层到输出层的线性可分。一旦隐层节点确定,可求解线性方程组得到输出权值。当RBF 神经网络隐性节点足够多时,将以足够高的精度逼近紧集上的连续函数[4-5]。

图2 RBF 神经网络结构图
由式(2)可以得出隐层第i 个神经元输出为:
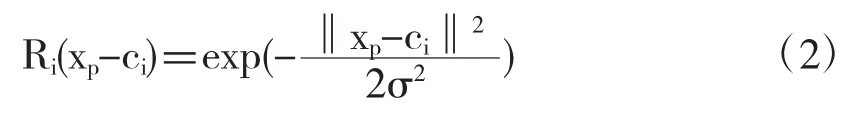
式中:x 表示n 维输入矢量;Ci表示基函数的中心点;σi表示基函数中心点的宽度。‖xp-ci‖表示xp-ci的欧几里得范数。
由RBF 神经网络结构图得出输出层第i 个神经元输出为:

式中:Q 为隐层节点数;yk为第 k 个输出;ωnm为隐层节点m 到输出层节点n 连接权值。
RBF 神经网络待定参数有基函数中心Ci、宽度σi、中心数目n 及隐层到输出层的连接权值ωnm。但是,在理论上很难准确求出RBF 神经网络结构参数的最佳值。
2.2 PSO 优化算法分析
作为一种基于群体智能的优化算法,PSO 算法不仅具备全局寻优能力,还具备良好的局部寻优能力[6-7]。
假设搜索空间为D 维,粒子总数为N,则粒子i的位置为 xi=(Xi1,Xi2,LXiD),飞行速度为 Vi=(Vi1,Vi2,LViD),个体目前为止所发现的最好位置为pbesti=(pi1,pi2,LpiD),种群所发现的最好位置 gbest=(g1,g2,LgD)。
粒子i 第d 维速度更新公式与位置更新公式分别为:

式中:d∈(1,D) 表示向量维数;ω 表示惯性因子,非常量,虽迭代次数增加不断减少;表示迭代次数;c1和c2为影响常数,分别表示个体和社会对其影响程度,通常取值[0,4];r1和 r2为在[0,1]之间随机产生的常数,避免学习迅速达到局部极值。在搜索空间里,常对粒子设置区间[Vmin,man],以对粒子进行限制。
惯性因子ω 计算公式为[8]:

式中:Iter 为设定的迭代总数;Iterman为 ω 达到最大迭代次数;当初始迭代权重ωman=0.9,最终迭代权重ωmin=0.4 时,可确保粒子群在开始搜索阶段具备较好的全局搜索能力,后期阶段具备良好的局部搜索能力。
粒子适应度为第d 次迭代后网络实际输出值与期望值之间的误差平方和,计算公式为:
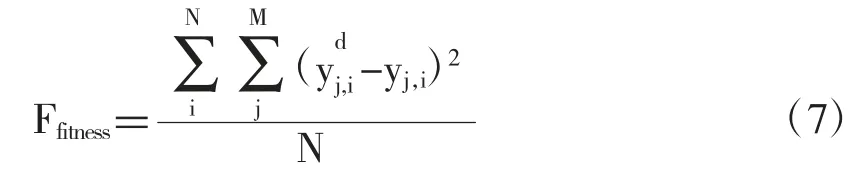
式中:N 为训练样本数;M 为RBF 神经网络输出层节点数为输出节点 j 的期望值;y 为节点j,ij,样本i 训练的实际输出值。
PSO 算法优化RBF 神经网络具体流程如图3所示:

图3 PSO 算法优化RBF 神经网络流程图
3 对比实验结果分析
3.1 参数选择
(1)实验对象

电池型号 额定容量电池类型 标称电压CGR18650CG LiFePO4 2100mAh 3.6V
(2)测试方式:仿真测试采用Matlab 软件中神经网络工具箱功能;实测采用某公司生产的多功能电池检测设备。
(3)测试参数:主要测试电池外部环境温度(T)、电压(V)、电流(I)、内阻(R)。
(4)测试数据:共采集400 组数据,其中测试样本随机抽取20 组,其余为训练样本。
3.2 实验结果对比
(1)拟合精度对比

图4 未进行PSO 算法优化的RBF 网络神经预测值与实测值对比
由图4 与图5 对比可以得出,经PSO 算法优化后,RBF 网络神经拟合精度相比未经过PSO 算法优化过的RBF 网络神经拟合精度要高。
(2)相对误差对比

图6 RBF 网络神经预测值与实测值相对误差

图7 PSO 算法优化的RBF 网络神经预测值与实测值相对误差
由图6 与图7 对比可知,经PSO 算法优化后的RBF 网络神经预测值与实测值相对误差很小,基本维持在-0.01~0.01 范围内,估算精度更高。
4 结 语
为提高电动汽车锂电池SOC 估算精度,将PSO算法引入到RBF 神经网络,建立基于PSO-RBF 神经网络混合估算算法。经过仿真实验结果与多功能电池检测设备实测结果对比分析可知,采用PSORBF 神经网络混合估算算法的的方式可有效提高锂电池SOC 估算精度。
