基于极值理论的沪深股市风险度量
2020-08-17杜诗雪唐国强李世君
杜诗雪,唐国强,李世君
(桂林理工大学 理学院,广西 桂林 541006)
0 引 言
金融风险管理一直以来都是工商企业、 金融机构及学术界密切关注的热点问题。 金融危机的出现表明,风险是现实存在的[1]。 近三十年来,受经济全球化和金融创新的影响, 金融市场波动明显, 这使得金融风险管理成为工商企业和金融机构经营管理必需的工具和能力[2]。 风险价值(VaR)是当前市场上较为主流的金融风险测量方法。 国内外学者对风险度量研究已经取得了丰厚的成果: 龚锐等[3]认为中国股票市场并不服从于简单的正态分布, 建立了在正态分布、t分布和GED分布下的GARCH族模型的风险价值; Orhan等[4]用GARCH族模型对股票市场进行了风险价值的对比研究; 张颖等[5]运用CAViaR模型[6]对我国股市和国外成熟市场进行了实证研究; 简志宏等[7]则对比了加入极值理论的CAViaR模型和GARCH-EVT模型, 发现CAViaR-EVT模型能更好地描述我国股市隔夜风险; 刘亭等[8]发现加入分位数回归的QR-t-GARCH模型比未加入分位数回归的t-GARCH模型效果更好; 唐勇等[9]用核拟合优度统计法和平均超额分布函数图分别选取阈值, 对低频数据和高频数据分布拟合了POT模型, 认为用核拟合优度统计法选取阈值比较有效; 张虎等[10]用极值理论对沪深股市收益率的风险价值进行研究; 王淼等[11]对沪市收益波动和厚尾性的条件风险价值(CVaR)进行研究。 在Harvey等[12]提出了Beta-skew-t-EGARCH模型和Gamma-skew-GED-EGARCH模型的基础上, 侍成等[13]比较了GARCH-t、 EGARCH-t、 GJR-GARCH-t和Beta-skew-t-EGARCH模型下的VaR; 张保帅等[14]发现Beta-skew-t-EGARCH-POT模型能有效提高极值风险的预测精度; 孙召伟等[15]将Copula函数和非对称Laplace结合研究上证指数和深证成指的VaR和CTE。
目前, 同时考虑收益率的尖峰、 肥尾特性、 杠杆效应和厚尾性的文献相对较少, 为了全面考虑收益率序列, 同时考虑极端值的VaR, 本文将极值理论与GARCH模型进行结合, 比较EGARCH-t模型、 EGARCH-t-POT模型和Beta-skew-t-EGARCH-POT模型在95%和99%置信水平下的VaR,并实证检验模型的精度和有效性。
1 理论介绍
1.1 EGARCH-t模型
为了反映金融市场波动的非对称性,Nelson[16]提出了指数条件异方差模型EGARCH(p,q)。本文采取低阶的EGARCH(1,1)模型
(1)
EGARCH-t模型的VaR计算公式为
VaR=μt+t1-p,vσt,
(2)
其中:μt和σt为收益率的条件均值和条件标准差,t1-p,v是自由度为v的t分布的1-p分位数。
1.2 EGARCH-t-POT模型
EGARCH-t-POT模型:提取EGARCH-t模型标准化残差,选取适当的阈值,对超过阈值的数据拟合广义帕累托分布(GPD)。定义超越期望函数为
(3)
其中,Nu是残差值超过阈值u的数据个数,即超越量;xti是对应收益率的值。 超越期望函数选择阈值的标准为阈值u足够大,在xti>u之后的超越期望函数曲线近似线性[17]。
假设日对数收益率为r1,r2, …,rn, 分布函数为F(r),xi=ri-u为超越量, 超越量x的分布函数表示为
(4)
式中,Pr表示概率, 将式(4)变换可得
F(r)=F(x+u)=[1-F(u)]Fu(x)+F(u),r>u。
(5)
对于一个充分大的阈值u,Fu(x)可用广义帕累托分布(GPD)近似。 GPD分布包括形状参数ξ和尺度参数β,可表示为
(6)
对于分布函数F(r), 可用经验估计值(n-Nu)/n来近似, 则可以得到实际样本的分布函数为
(7)
解出上述分布函数分位数,则EGARCH-t-POT模型的VaR计算公式为
(8)
1.3 Beta-skew-t-EGARCH-POT模型
为了更好地描述金融时间序列的尖峰、肥尾、偏斜、非正态、波动率聚集以及杠杆效应,Harvey和Sucarrat在2014年提出Beta-skew-t-EGARCH-POT模型[12]:
(9)

Beta-skew-t-EGARCH-POT模型标准化过后的残差为resid, 在置信水平p下金融产品的VaR为
(10)

1.4 VaR的返回检验[2]
VaR的准确率检验是指VaR模型的测量结果对实际损失的覆盖程度。例如,假设事先给定置信区间为95%,则VaR的准确性是指实际损失结果超过VaR的概率是否小于5%。VaR的准确率检验方法有失败率检验法、 区间预测法、 分布预测法、 超额损失大小检验法、 方差检验法、 概率预测法和风险轨迹预测法等。 本文采用Kupiec[18]提出的失败率检验法测量VaR计算的准确程度。 构造检验统计量
(11)
其中:p为显著性水平;N为失败天数;T为观测总天数, 则失败频率为N/T。 假设计算VaR的置信度为c, 则模型的准确性评估就转变为检验失败频率N/T是否显著不同于1-c。 在原假设的条件下,LR统计量应服从自由度为1的卡方分布。如果计算出的LR大于卡方统计量的临界值,就拒绝VaR有效的原假设。
2 上证指数收益率风险度量
2.1 数据选取和描述性统计
为了检验上述模型的精度和有效性,选取沪市上证综合指数2009年1月5日—2018年11月16日的日收盘价,共2 401个数据作为研究数据。假设t时刻的收盘价为Pt,由于收益率序列比收盘价序列具有更好的统计特征,本文对收盘价取对数再进行差分运算即可得到日收益率rt=lnPt-lnPt-1,共2 400个数据(图1)。数据来自国泰安数据库,均采用R软件分析。

图1 上证综合指数日收盘价和日收益率Fig.1 Daily closing value and daily return of Shanghai Composite Index
偏度是统计分布非对称程度的特征, 由表1可以看出, 收益率偏度为负值, 具有左偏特征。 根据边宽江等[19]的检验方法对尖峰、 厚尾进行检验, 峰度为5.057 111>3, 具有尖峰的特征。 J-B统计量p值小于显著性水平0.01, 拒绝正态和无尖峰的原假设。由图2的Q-Q图中也可以明显看出收益率不服从正态分布,且图中上下两端数据均偏离直线,表明收益率尾部具有厚尾性。ADF检验和P-P检验表明,序列是平稳的;Ljung-Box检验显示在0.05的显著性水平下,收益率序列不存在自相关。日收益率图中可以看出波动率聚集特征,对收益率序列进行ARCH效应检验,结果表明收益率序列具有条件异方差性。

图2 上证综合指数日收益率Q-Q图Fig.2 Q-Q plot of Shanghai Composite Index
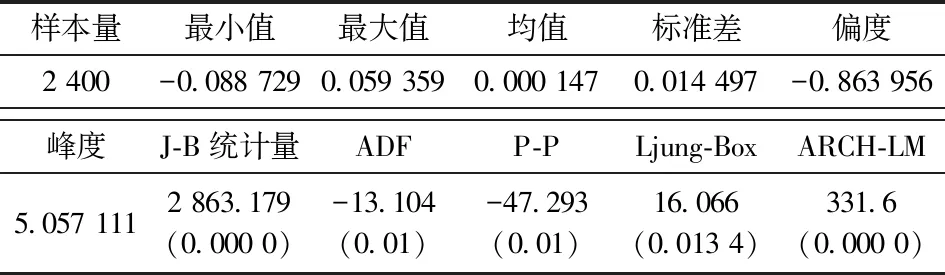
表1 上证综合指数的日收益率描述统计量Table 1 Descriptive statistics of daily closing value of Shanghai Composite Index
2.2 模型建立
2.2.1 EGARCH(1,1)-t模型建立 由于上证综合指数序列具有非对称性和异方差性, 且t分布相对于正态分布和广义误差分布(GED)能更好地反映收益率特征, 建立EGARCH(1,1)-t模型,通过极大似然估计法估计出模型参数及参数显著性检验值,如表2所示。

表2 EGARCH(1,1)-t模型参数估计Table 2 Parameters estimation of EGARCH(1,1)-t model
可见, 除了参数α的p值没有通过检验之外, 其余参数均通过显著性检验。 收益率的参数
值(ω=-0.056 603)非常小, 说明市场的风险很大。 将参数估计值带入式(1), 即可得到EGARCH(1,1)-t模型的条件方差方程
(12)
2.2.2 EGARCH(1,1)-t-POT模型建立 由上述EGARCH(1,1)-t模型可以得到标准差的估计。 由于EGARCH(1,1)-t模型度量的是正常市场中的风险, 而现实情况中往往是少数的极端值却可能造成巨大的损失。 因此, 对EGARCH(1,1)-t模型的标准化残差建立EGARCH(1,1)-t-POT模型,即对超过阈值u的数据进行建模。建立POT模型最重要的就是阈值的选择,阈值选择过大会造成尾部数据太少,估计出的参数的方差就会很大,精度变差;相反,如果阈值选择太小,就会把靠近中心的数据用来拟合,造成有偏的参数估计[20]。选取阈值的方法一般采用超越期望函数图法,要求超过阈值部分呈现线性特征。另外,DuMouchel等[21]提出的10%原则:在阈值u允许的情况下,选取10%左右的数据作为要研究的极端值数据。
根据超越期望函数(图3), 综合DuMouchel提出的10%原则, 可以看出在标准化残差大于1.6之后超越期望函数图呈线性趋势。 因此, 选择阈值1.6较为合理。 对于超过阈值的数据拟合广义帕累托分布(GPD), 得到形状参数ξ和尺度参数β的估计结果(表3)。为了检验模型的拟合效果,对EGARCH(1,1)-t模型的标准化残差建立POT模型,诊断检验如图4所示。散点和拟合线越接近说明模型拟合得越好,可以看出,大部分散点都落在拟合线上或附近,极少部分点与拟合线有微小的偏差,说明模型拟合效果良好,这也说明选取阈值1.6是合理的。

图3 EGARCH(1,1)-t模型的超越期望函数图Fig.3 Mean excess plot of EGARCH(1,1)-t model
图4 EGARCH(1,1)-t-POT模型诊断检验图Fig.4 Diagnostic test plot of EGARCH(1,1)-t-POT model

表3 EGARCH(1,1)-t-POT模型参数估计Table 3 Parameter estimation of EGARCH(1,1)-t-POT model
2.2.3 Beta-skew-t-EGARCH-POT模型建立 对上证综合指数日对数收益率序列拟合Beta-skew-t-EGARCH模型,结果如表4所示。参数ω是长期波动的常数项;φ是持续性参数, 数值较大说明波动的丛集性较强;κ1是ARCH参数, 其绝对值越大说明波动对冲击的反应越大;κ*是杠杆参数,说明收益率序列具有杠杆效应;参数df和skew分别是模型自由度和偏度参数[14]。

表4 Beta-skew-t-EGARCH模型参数估计Table 4 Parameter estimation of Beta-skew-t-EGARCH model
对Beta-skew-t-EGARCH模型的残差进行标准化,再建立POT模型。 从图5中可以看出, 超越期望函数图在某个临界值之后开始呈现线性趋势, 选取阈值为1.5, 得到POT模型的形状参数ξ和尺度参数β的估计结果如表5。 为了检验模型的拟合效果, 对Beta-skew-t-EGARCH模型的标准化残差建立POT模型, 诊断检验如图6所示, 散点和拟合线越接近, 说明模型拟合得越好, 可知大部分散点都在拟合线上,极少部分点与拟合线有微小的偏差,说明模型的拟合效果较好。
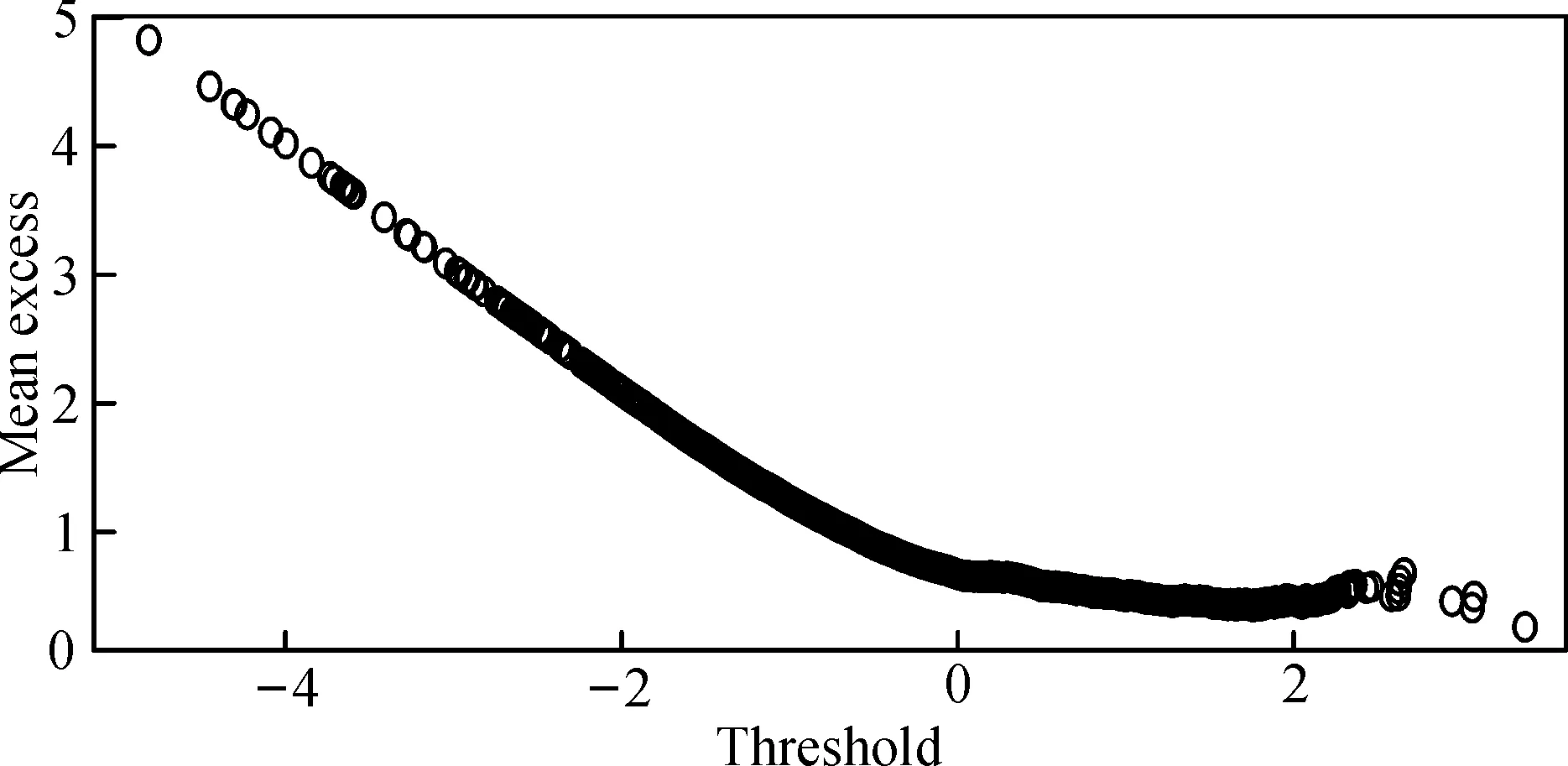
图5 Beta-skew-t-EGARCH模型的超越期望函数图Fig.5 Mean excess plot of Beta-skew-t-EGARCH model

图6 Beta-skew-t-EGARCH-POT模型诊断检验图Fig.6 Diagnostic test plot of Beta-skew-t-EGARCH-POT model

表5 Beta-skew-t-EGARCH-POT模型参数估计Table 5 Parameter estimation of Beta-skew-t-EGARCH model
2.3 VaR计算和返回检验
Kupiec[18]提出的失败率检验法认为: 当VaR低于实际损失则记为一次失败事件; 反之, 当VaR超过实际损失则记为一次成功事件。 实际失败率p等于失败天数N除以观测总天数T。 模型原假设为H0:p=N/T=α, 其中α是显著性水平。 当实际失败率p小于给定的显著性水平α, 则高估风险; 反之, 当实际失败率p大于给定的显著性水平α,则低估风险。 对各模型进行VaR计算, 结果见表6。

表6 各模型的失败率及LR统计量Table 6 VaR value and statistic LR of models
从整体来看, 各模型失败率都小于显著性水平, 说明各模型都有不同程度上的低估风险。 从各模型失败率的表现来看, 在显著性水平为0.05和0.01下, 表现最差的都是EGARCH-t模型; 但在加入了极值理论后的EGARCH-t-POT模型, 失败率表现得更为接近显著性水平。 对于Beta-skew-t-EGARCH-POT模型来说, 失败率在显著性水平为0.05下较EGARCH-t-POT模型有所提升, 但是在较低的显著性水平0.01下, 失败率并没有表现得更好。 就似然比统计量LR来说, 在显著性水平为0.05和0.01下, 卡方临界值分别为3.841和 6.635, 只有EGARCH-t模型在0.05的显著性水平下, 8.020 239>3.841, 预测准确率不高。 其余模型在显著性水平为0.05和0.01下都接受原假设, 认为VaR是有效的。
3 深证指数收益率风险度量
选取2009年1月5日—2018年11月16深证成分指数的日收盘价作为研究对象,具体分析过程同第2节。对深证成分指数建立EGARCH(1,1)-t模型,得到模型参数估计如表7。

表7 EGARCH(1,1)-t模型参数估计Table 7 Parameter estimation of EGARCH(1,1)-t model
从上述模型参数估计表来看,所有参数均通过了显著性检验,将参数估计值带入式(1), 得到深证成分指数的EGARCH(1,1)-t模型的条件方差方程
(13)
对EGARCH(1,1)-t模型的标准化残差建立EGARCH(1,1)-t-POT模型,根据超越期望函数图和DuMouche10%原则,选择阈值为1.35,对超阈值的数据建立POT模型,结果如表8所示。

表8 EGARCH(1,1)-t-POT模型参数估计Table 8 Parameter estimation of EGARCH(1,1)-t-POT model
对深证成分指数收益率序列拟合Beta-skew-t-EGARCH-POT模型。同样,根据超越期望函数图和DuMouche10%原则,选择阈值为1.35,得到模型参数估计如表9所示。
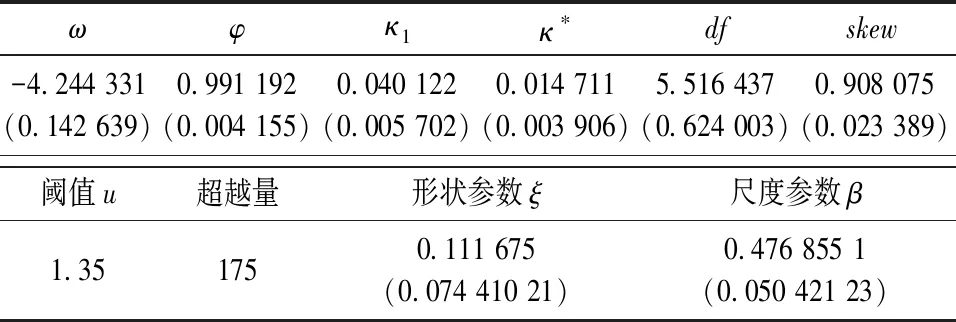
表9 Beta-skew-t-EGARCH-POT模型参数估计Table 9 Parameter estimation of Beta-skew-t-EGARCH-POT model
分别对上述3个模型进行VaR计算和失败率检验,结果见表10。从整体来看,各模型失败率都小于显著性水平,说明3个模型都有不同程度上的低估风险。从各模型失败率的表现来看,无论是在显著性水平为0.05还是0.01,表现最差的都是EGARCH-t模型;但加入了极值理论后的EGARCH-t-POT模型在两个显著性水平下,失败率都更为接近显著性水平,这一点与沪市一致。对于Beta-skew-t-EGARCH-POT模型来说,在显著性水平0.05下,相对于EGARCH-t-POT模型失败率表现更好,这一点与沪市也是一致的;但是在较低的显著性水平0.01下,则不然。只有EGARCH-t模型在0.05的显著性水平下的LR统计量值7.453 078>3.841,预测准确率不高。其余模型在显著性水平为0.05和0.01下LR统计量都是小于卡方临界值的,不拒绝原假设,说明预测准确率较高,认为VaR有效。

表10 各模型的失败率及LR统计量Table 10 VaR value and statistic LR of models
4 结 论
通过沪市和深市的日收益率的风险价值分析,运用EGARCH-t模型、EGARCH-t-POT模型和Beta-skew-t-EGARCH-POT模型,分别计算在95%和99%两种置信水平下的VaR。3种模型的侧重点各有不同,EGARCH-t模型主要刻画了金融时间序列的非对称性和杠杆效应。EGARCH-t-POT模型则在提取EGARCH-t模型标准化残差的基础上加入了极值理论,能够很好地刻画日收益率剩余波动的影响,体现分布的“厚尾性”。Beta-skew-t-EGARCH-POT模型综合了GRACH族模型的优点,同时加入对模型尾部拟合较好的POT模型,能够很好地刻画金融时间序列特征。通过3种模型的实证研究及对比分析,得出以下结论:
(1)我国股票市场的收益率分布总体上具有尖峰、肥尾、非对称性和波动集聚性的特征。从侧面证明了用正态分布去刻画收益率序列是不充分的。因此,如何选取合适的模型去描述金融数据的特征,也是一个需要重点研究的问题。
(2)加入极值理论的POT模型对收益率尾部分布进行拟合,得出的结论是VaR值更接近于给定的显著性水平,风险度量的效果会更好。但是,关于阈值的选取,仅仅依靠观察超越期望函数图未免有些主观,需要综合多种方法进行选择。
(3)Beta-skew-t-EGARCH-POT模型目前应用的还很少,但对其标准化后的残差序列拟合极值理论的广义帕累托分布(GPD),得到的VaR值在95%置信水平下表现最好,但在99%置信水平下表现并没有比EGARCH-t-POT模型更好。
(4)通过似然比统计量LR进行返回检验,发现只有EGARCH-t模型在95%置信水平下的VaR值没有通过检验,其余模型在95%和99%两种置信水平下的VaR值均通过了检验,认为其VaR值是有效的。
