机械臂运动的智能自适应模糊控制策略

赵 娟，杨慧中

（1.无锡工艺职业技术学院，江苏 宜兴 214206；2.江南大学，江苏 无锡 214122）

1 引言

机械臂可以代替人类进行重复性生产活动，而且随着智能化程度越来越高，对机械臂的控制精度要求也越来越高，但是外界环境变化产生的扰动会影响机械臂的控制精度，导致产品质量下降[1]。因此研究机械臂控制技术具有重要意义。随着人工智能的兴起与发展，人工智能技术与传统控制理论相结合，并将其应用到机械臂控制中成为一个热点研究方向。文献[2]使用抗饱和神经网络动态面控制法解决了机械臂外界扰动及输入受限问题；文献[3]设计了干扰观测器与滑模控制相结合的机械臂控制方法，解决了滑模控制抖振问题；文献[4]使用两个RBF 神经网络设计了自适应控制器，其中一个为输入端控制器，另一个为辨识器，最终提高了机械臂末端连杆控制的稳定性；文献[5]提出了RBF 神经网络算法非线性积分滑模控制方法，不仅减小了跟踪误差而且减小了驱动转矩波动幅度。以上研究成果使用不同方法解决了机械臂轨迹跟踪控制问题，且设置了不同的控制目标，达到了不同的控制效果。针对存在外界干扰情况下的轨迹跟踪控制问题，以二阶模糊控制器为基础，提出了具有智能自适应调节能力的模糊控制器，最终实现了减小控制误差且减小驱动力矩幅值的目的。

2 双连杆机械臂动力学模型

2.1 双连杆机械臂结构

双连杆机械臂系统结构，如图1 所示。将机械臂工作区域设置在竖直平面内，此机械臂由两个关节组成，其中连杆1 与基座间关节记为关节1，连杆1 与连杆2 之间的关节记为关节2，每个关节仅有一个自由度。

图1 双连杆机械臂模型Fig.1 Two-Joint Manipulator Model

图中：m1、m2—连杆 1 与连杆 2 的质量；l1、l2—连杆 1 和连杆 2 的长度；θ1、θ2—关节 1 和关节 2 的关节角；g—重力加速度。

2.2 机械臂动力学模型

使用拉格朗日方程[6]建立双连杆机械臂系统的动力学方程，为：

式中：θi—关节的 i 角位置；τi—关节 i 的驱动力矩拉格朗日函数—机械臂系统总动能；V（θ）—机械臂系统总势能。刚性机械臂系统动能和势能的计算较为简单，且研究已经成熟，可参考文献[7]，这里不再赘述，直接给出动力学方程求解结果，为：

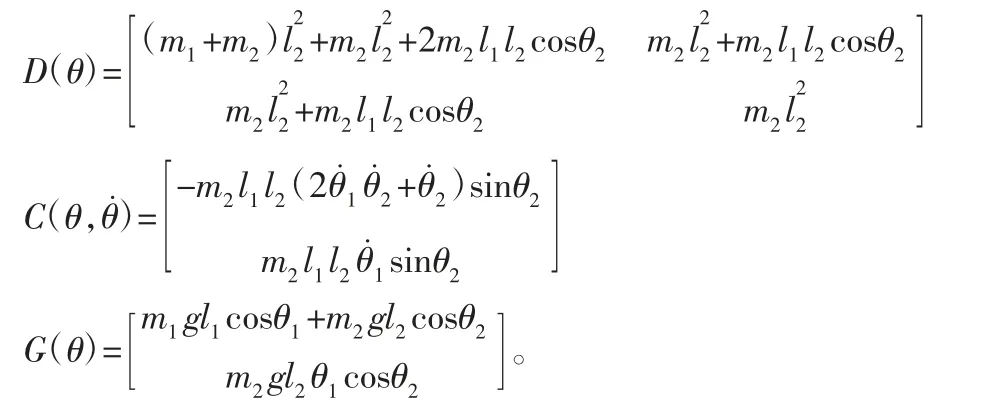
3 智能自适应模糊控制器

3.1 机械臂系统控制方案

记机械臂期望运动轨迹为θd，实际运动轨迹为θ，则轨迹跟踪误差及误差变化率为：

机械臂轨迹跟踪控制的目标是通过设计控制律使用最小的力矩实现最小的跟踪误差。也就是说，控制律的设计依赖跟踪误差而变化，因此将轨迹跟踪误差e 及误差变化率e˙作为模糊控制器输入，将机械臂控制律u 作为模糊控制器输出。

使用智能自适应模糊控制器对双连杆机械臂系统的控制方案及智能自适应模糊控制器的设计方案，如图2 所示。图中：Ke、Ke˙—量化因子；Ku—比例因子。智能自适应模糊控制器的设计思路为：以跟踪误差和驱动力矩最小为目标，以Ts为周期实时调节模糊控制器参数，使参数能够随跟踪误差和驱动力矩变化而自适应调节，最终达到减小跟踪误差和驱动力矩的目的。

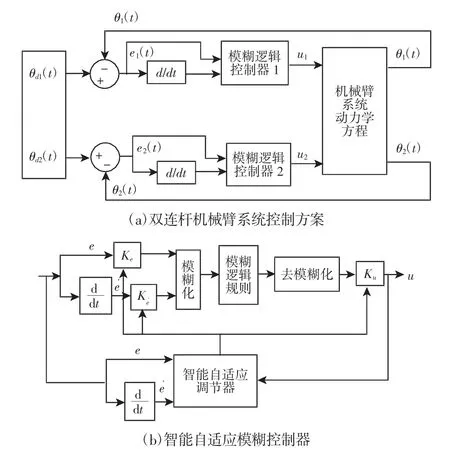
图2 机械臂控制方案及模糊控制器设计Fig.2 Manipulator Control Scheme and Fuzzy Controller Design

3.2 智能自适应模糊控制器实现

从图2（b）中可以看出，模糊逻辑控制器的核心内容包括两个部分：一是模糊控制器设计，二是智能自适应调节器设计，其中模糊控制器可分为三个部分：精确量的模糊化、模糊逻辑规则制定、去模糊化[8]，本节只对模糊控制器进行设计，智能自适应调节器在第4 节进行设计。为了提高模糊控制精度，将轨迹跟踪误差e、误差变化率e˙、机械臂控制律在论域上模糊化为7 个语言值，分别为负大（NB）、负中（NM）、负小（NS）、零（ZE）、正小（PS）、正中（PM）、正大（PB）。模糊化隶属度函数使用高斯隶属度函数：

式中：μ（x）—x 的隶属度值；c—隶属度函数均值；σ—隶属度函数偏移量。

模糊逻辑规则的制定遵循两条规则：（1）当误差为较大正值（或负值），且误差变化律也为较大正值（或负值），输出量为较大的正值（或负值），以减小误差；（2）当误差为较大正值（或负值），而误差变化律为负值（或正值）时，输出为较小正值（或负值）或0。按照以上两条规则，制定模糊规则，如表1 所示。

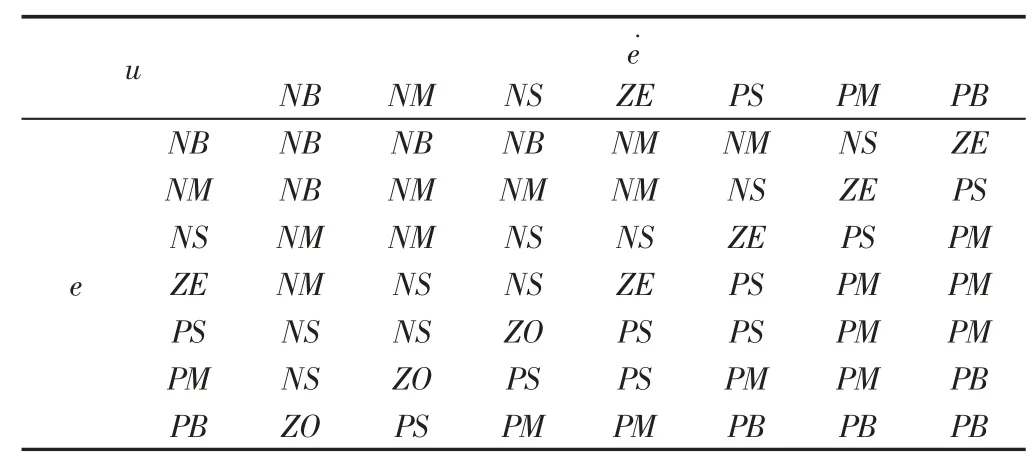
表1 模糊逻辑规则Tab.1 Fuzzy Logistic Rule

由于加权平均法充分利用了隶属度最大元素提供的主导信息，因此选用加权平均法进行解模糊化[9]，即：

式中：z*—去模糊化后的参数；n—模糊元素的个数；ϖj—模糊集的元素；μ（ϖj）—元素ϖj的隶属度。

4 智能自适应调节器

为了使模糊控制器具有智能自适应性，能够随控制结果的变化自适应调节自身参数和状态，设计了智能自适应调节器。此调节器以跟踪误差和驱动力矩最小为目标，提出了多策略协同进化粒子群算法进行求解，将求解结果反馈给模糊控制器，从而实现模糊控制器的智能自适应性。

4.1 基本粒子群算法

基本粒子群算法中，粒子速度在自身惯性、自身历史最优和种群最优位置的牵引下进行更新[10]，即：

式中：vid（t）、xid（t）—粒子 i 迭代 t 次时在 d 维上的速度和位置；pid—粒子i 迭代至当前时刻在d 维上的最优位置；pgd—种群迭代至当前时刻在d 维上的最优位置；c1、c2—自身学习因子和种群学习因子；rand（）—（0，1）间的随机数。

4.2 多策略进化与多种群协同

根据惯性权重对粒子探索能力的影响，设置三种进化策略，分别为大范围搜索策略、精细搜索策略和速度自适应更新策略。

4.2.1 多策略进化

在粒子寻优过程中，惯性权重对粒子的探索能力和开发能力影响较大，惯性权重较大时粒子的探索能力较强，能够大范围移动，而探索之前未到达区域，利于全局搜索；惯性权重较小时粒子的开发能力较强，能够在某一区域精细搜索，利于局部搜索和算法收敛。

对于同一搜索策略下的粒子，希望粒子的惯性权重随着算法的迭代而不断调整，从而动态调整算法的探索能力和开发能力，使用线性递减方法自适应调整惯性权重，即：

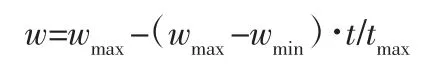
式中：w—自适应权重；wmax、wmin—惯性权重最大和最小值；tmax—最大迭代次数。

通过设置不同的惯性权重最值，实现不同搜索策略，即大范围搜索策略的惯性权重变化为：

细致搜索策略的惯性权重变化为：

当本次搜索的粒子优于上一代搜索粒子时，按照基本粒子群算法中速度更新方法依然要改变搜索方向，这种不加区分的粒子搜索方法显然不合理，因此设置速度自适应更新策略，基本思想为：当本次搜索的粒子优于上代粒子时，依然沿此方向继续搜索；当本次搜索粒子次于上代粒子时，则在历史最优和种群最优牵引下运动。速度自适应更新策略为：

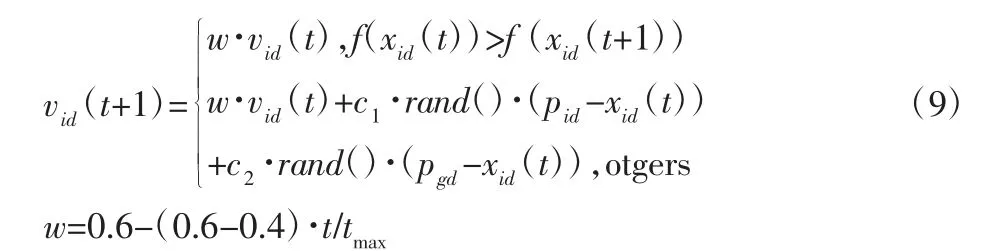
式中：f（x）—适应度函数。

4.2.2 多种群协同

式（7）给出了大范围搜索策略，具有强探索能力；式（8）给出了细致搜索策略，具有强开发能力；式（9）给出了速度自适应更新策略，具有快速搜索能力。若单独使用细致搜索策略，算法能够在小范围内精细搜索，但是难以从一个区域运动至另一区域进行大范围搜索；同样的，单独使用大范围搜索策略，粒子大范围浏览区域，而没有进行细致搜索，难以搜索到最优解。因此提出了多种群协同搜索方法，将整个粒子种群划分为3 个子群，按照3 种搜索策略分别设置3 个子群的速度更新机制，每完成一次迭代通过共享子群最优信息实现信息交流。

4.3 多策略协同进化粒子群算法流程

根据基本粒子群算法原理、多策略进化和多种群协同搜索方法，制定多策略协同进化粒子群算法流程为：

（1）初始化算法参数，包括种群规模、粒子维度、搜索区域等；

（2）将种群等分为3 个子群，将3 个子群的粒子进行随机初始化；

（3）各子群按各自搜索方式搜索最优位置，每完成一次迭代，交换子群最优粒子；

（4）比较子群最优粒子，挑选出种群最优粒子，使用种群最优粒子替换各子群最优粒子；

（5）是否达到最大迭代次数，若是则结束，输出种群最优粒子；若否则转至Step3。

4.4 智能自适应调节器实现

将多策略协同进化粒子群算法应用于模糊控制器的自适应调节中，模糊逻辑控制器包含3 个参数，因此将粒子维度设置为3，即 xi=（xi1，xi2，xi3）T，粒子的 1 至 3 维度分别表示 Ke、Ke˙、Ku。根据参数的通常取值，将搜索范围分别设置为［0，10］、［0，8］、［0，8］。

优化目标为使用最小的驱动力矩实现最小的跟踪误差，即目标函数为：

式中：g（）—目标函数；N—采样数量；e1（i）—关节 1 跟踪误差；e2（i）—关节 2 跟踪误差；u1（i）—关节 1 驱动力矩；u2（i）—关节2 驱动力矩；ϑ1=ϑ2=104—权值，目的是将误差调整至与力矩具有相同的数量级。

5 仿真验证

5.1 多策略协同进化粒子群算法验证

仿真实验在MATLAB 仿真环境下进行，机械臂参数设置为：m1=2kg、m2=1kg、l1=1.2m、l2=0.6m，g=9.8m/s2。关节 1 和关节 2的期望运动轨迹为 θd1（t）=θd2（t）=sin（2t-π/2）。关节角初始设置为 θ0=［-1，1］T，外界干扰设置为 y=sint。

以第一周期的参数自适应调节为例，分别使用多策略协同进化粒子群算法与传统粒子群算法对模糊逻辑控制器参数进行优化，算法的参数设置为：最大迭代次数tmax=500，粒子规模设置为99，学习因子c1=1.8、c2=2.2。分别使用多策略协同进化粒子群算法与基本粒子群算法优化模糊控制器参数，目标函数随迭代过程的变化曲线，如图3 所示。

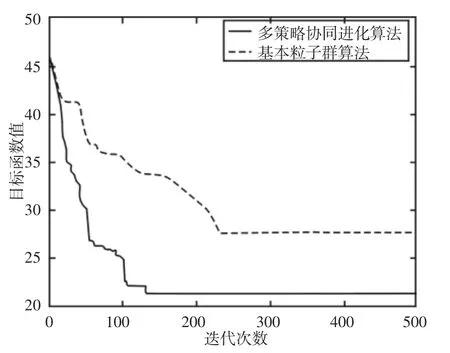
图3 模糊控制器参数优化过程Fig.3 Parameters Optimizing Process of Fuzzy Controller

从图3 可以看出，多策略协同进化算法在搜索最优参数过程中，不仅收敛速度快，而且最优收敛值也远远优于基本粒子群算法，转化到模糊控制问题中，多策略协同进化算法能够在较短时间内搜索到更优参数，且搜索的参数可以使用更小的力矩实现更小的跟踪误差。算法收敛速度快对于机械臂系统的实时控制具有重要意义。多策略协同进化粒子群算法之所以优于基本算法，是因为多策略进化方法和多子群协同搜索策略，兼顾了种群的探索能力和开发能力，既保证了算法的大范围探索能力，又兼顾了小范围开发能力，所以搜索的参数值优于基本粒子群算法，且收敛速度也较快。

使用两种粒子群算法最终搜索到的第一周期最优参数及目标函数值，如表2 所示。

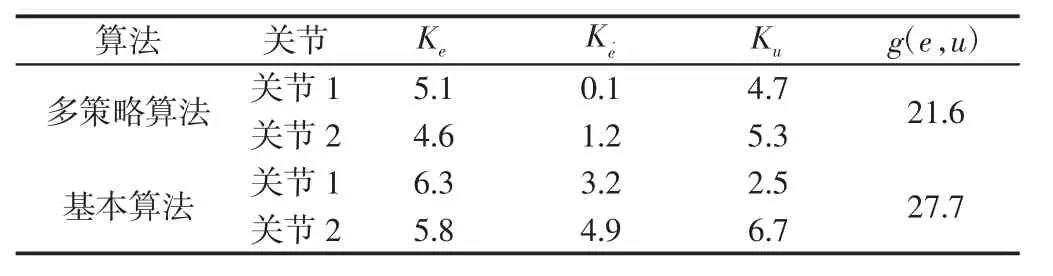
表2 算法搜索结果Tab.2 Algorithm Searching Result

5.2 控制结果与分析

为了形成对比效果，分别使用智能自适应模糊控制器和PID控制器对机械臂进行控制，得到的跟踪误差与驱动力矩曲线，如图4、图5 所示。从图4 可以看出，使用智能自适应模糊控制器对关节1 和关节2 产生的轨迹跟踪误差明显小于PID 控制器的控制误差。经统计，使用智能自适应模糊控制器对关节1 控制的最大跟踪误差为2.1×10-4rad，对关节2 控制的最大跟踪误差为1.9×10-4rad；而使用PID 控制器对关节1 的最大跟踪误差为7.9×10-4rad，对关节2 的最大跟踪误差为7.6×10-4rad，是智能自适应模糊控制器的4 倍左右。由图5 可以看出，PID 控制器驱动力矩波动较大，这是由正弦型外界干扰引起的，而智能自适应模糊控制器的波动振幅极小，在应对外界干扰时，能够以小范围浮动控制力矩实现机械臂控制。经统计，关节1 的控制力矩中，PID 控制力矩的平均波动幅度为18Nm，智能自适应模糊控制力矩平均波动幅度为3Nm；关节2 的控制力矩中，PID 控制力矩的平均波动幅度为10Nm，智能自适应模糊控制力矩平均波动幅度为1.5Nm，由此可见，智能自适应模糊控制器的力矩波动幅度远远小于PID 控制器。综上所述，智能自适应模糊控制器能够以更小的力矩实现更准确的轨迹跟踪控制，这是因为智能自适应模糊控制器能够根据控制误差和力矩大小实时优化模糊控制器，使模糊控制器能够根据控制结果实时改变自身参数，实现了在任意时刻和任意状态下的最优控制。

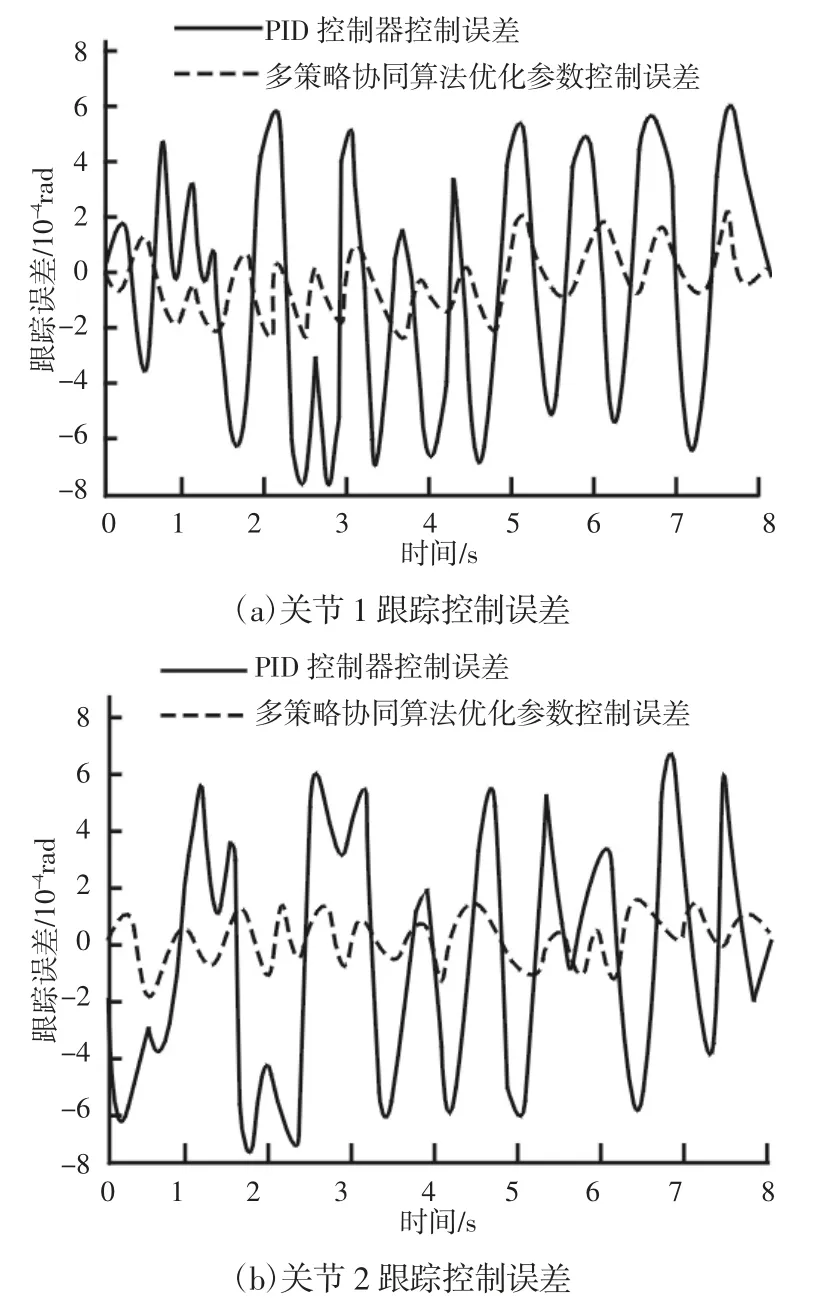
图4 两关节的跟踪控制误差Fig.4 Tracking Control Error of the Two Joints

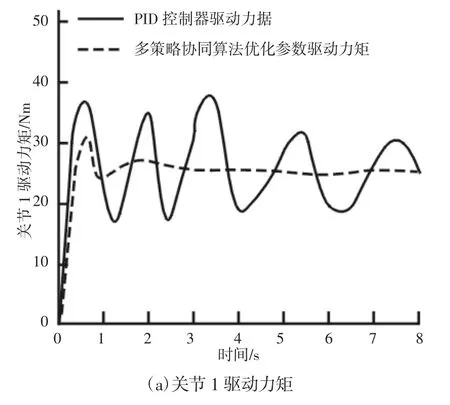
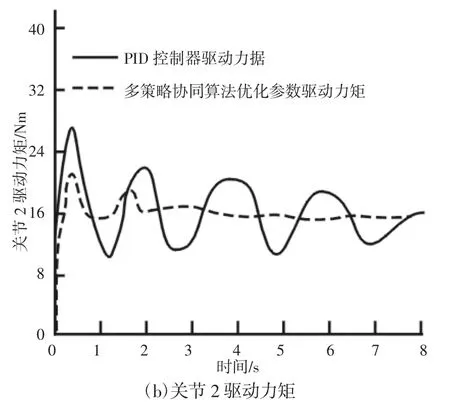
图5 两关节的驱动力矩Fig.5 Driving Torque of the Two Joints

6 结论

研究了机械臂轨迹跟踪控制问题，以二阶模糊控制器为基础，设计了智能自适应模糊控制器，实现了以最小力矩得到最小误差的控制目标。

经仿真验证，得到以下结论：（1）多策略协同进化粒子群算法通过多策略进化和多种群协同搜索方式，提高了算法的收敛速度和精度；（2）智能自适应模糊控制器能够根据控制结果实时调整自身参数，实现了任意时刻的最优控制。