一种新的摄像机线性标定方法

姚 阳，张 磊，徐冰辉，姚兴田

（南通大学机械工程学院，江苏 南通 226019）

1 引言

摄像机标定是指根据所给的摄像机模型，在图像像素坐标点与空间场景点位置之间建立对应的关系，对其内部参数及外部参数进行求解的过程[1]。摄像机对标定板上特征点的图像进行采集，再利用特征点的世界坐标及其相应的图像坐标即可得出摄像机参数。

目前摄像机标定技术大概可分为两类[2]：（1）传统摄像机标定法，利用标定板确定摄像机参数；（2）自标定，即根据摄像机运动过程中所产生的两图像间的对应关系进行标定。传统标定法标定精度较高，操作较为简便，但是对标定模块要求较高。自标定法不倚靠于标定参照物，灵活性较高，但约束条件较强，标定繁琐，且标定精度较低，鲁棒性不足。

常用摄像机标定方法有 Faugeras 标定法[3]，Tsai 两步法[4]，张正友平面标定法[5]。Faugeras 的线性模型摄像机标定方法是基于线性方程组的最小二乘问题。Tsai 标定法需要预先得到一部分参数值，先通过线性方法求解出部分参数，再通过非线性优化解出剩余摄像机参数的精确解。张正友标定利用平面标定板在不同视角下的多幅图像，依据设计的单应矩阵，标定得到摄像机参数。这两种方法一般可获得其免费的程序包，使得用户使用方便。但由于程序包封装，只适合于静态标定。一旦参数发生改变，需重新标定。如对于焦距等参数随时改变且需要实时标定参数的交通保安视频监控、机器人视觉等场合，这两种方法的程序包并不适用。若用户自行开发，实现并不容易。再者，Tsai 标定法所要求的参数，有时厂家并不提供，像素间距也不易把握。因此类似Faugeras 的线性标定法在实时场合仍然有较高应用价值，用户便于针对性的开发自己的软件。

较多文献针对标定精度不高的问题开展了研究工作：文献[6]将主点定在图像中心，同时设纵横比为1，通过改进的线性方法得出摄像机坐标，然后根据摄像机坐标系下的三维点对内外参进行优化。文献[7]在根据两步法得到初始标定值的基础上，再对全部参数进行非线性优化，求解出最终的标定结果。文献[8]提出一种新的畸变模型，将多种镜头畸变考虑在其中，并用迭代法解出精确解。上述文献中，可以看出近些年的标定更多是从考虑畸变，优化算法等方面改进，而在线性标定阶段较少进行改善，导致标定一开始就偏差较大，需要依赖后期的优化。此外利用非线性优化法进行参数标定用时较多，且算法复杂。有的是基于Tsai 标定法进行的后续改进，若参数一旦发生变化，需重新标定，过程显得繁琐，更不能应用在实时场合。

在参数随时发生变化的场合，在相对简单的线性标定方法的基础上再考虑畸变因素，往往可以获得易实现与精确度的双赢。Faugeras 是线性标定方法的代表，其实现简单。但该方法未考虑摄像机特性，对于摄像机标定模型只当成一般数学问题求解，并且将不同量级的参数混合，导致误差放大，尤其是求解的图像中心点与实际的图像中心有一定偏差，有时偏差很大。根据上述分析，对Faugeras 标定法进行了改进，利用摄像机参数的特点，提出了一种新的线性标定方法，可以分步求解摄像机内外参数，并在标定过程中对部分参数进行优化。

2 Faugeras 标定中存在的问题

2.1 传统的Faugeras 标定法

Faugeras 等在1986 年提出基于线性成像模型的摄像机标定方法对摄像机内外参数进行标定。该方法将一个三维目标物放置于摄像机前，该目标物上的每一个顶点均可作为特征点，摄像机获取目标物上特征点的世界坐标和相应的图像坐标即可计算出摄像机的内外参数。

该摄像机标定方法，采用内参数为四参数的摄像机模型，世界坐标系OWXWYWZW建立在标定参照物上，假设选取的特征点世界坐标已知，可得：

式中：（u，v）—特征点在摄像机图像坐标系中的坐标；（xw，yw，zw）—特征点在世界坐标系中的坐标。

将上式展开并消去zc得：

在世界坐标系中，对于n 个已知坐标的特征点，则可由式（2）得到2n 个方程构成的方程组，如下：

根据Faugeras 传统的方法，由于m34≠0，两边同除以m34，该方程可简化表达为：Am′=B，式中：m′=m/m34。运用最小二乘法解得：m′=（ATA）-1ATB。

2.2 存在的问题

通过上述求解过程，可发现Faugeras 先行求解间接向量m′，然后根据，求解m34。此时误差已引入，且误差较大，另外由它产生的其它参数误差也相应较大。Faugeras 方法缺点是对于摄像机标定模型只当成一般数学问题求解，将各个参数混在一起形成m 向量，并先解出该向量，容易使不同数量级的参数混合，造成误差增大。而且规定采集的图像像素点不能在同一平面上，否则造成参数求解残缺。若采用平面的多个像素点求解，一般仍然需要两个不同平面的像素点来补足参数，共同求解。

3 新的线性标定法

Faugeras 的方法未利用在标定时，已经存在的现成条件或者近似条件，比如对于绝大部分相机，可以认为，或者规定相机中轴就穿过图像的中心点，即（u0，v0），因此可以近似认为 u0，v0是已知，这样内参数只剩下kx与ky，而这两个值一般很接近，甚至也可用一个值表达，如此，内参几乎只剩一个参数。加上外参数的旋转向量之间有约束非独立，这可以被利用来求解，可避免Faugeras 将其混合起来的做法，有利于参数求解精度的提高。

提出的新方法如下，根据式（2）列出基本方程组：将m14及m24单独放在右边，考虑m14，m24不带其它参数，虽然其本身带的内外参数不少，但在下面的推导中可以将其进行处理，利于问题的求解。

（4）式中的第一式两边同除以m14，若有n 个像素点，可形成方程组如下：

所以前述方程组可记为向量与矩阵形式：Aumu=Bu。式中：Au-n×7 矩阵，Bu-n 行的列向量。

通过最小二乘法解出mu 向量后，根据式（1）与式（6）可知：

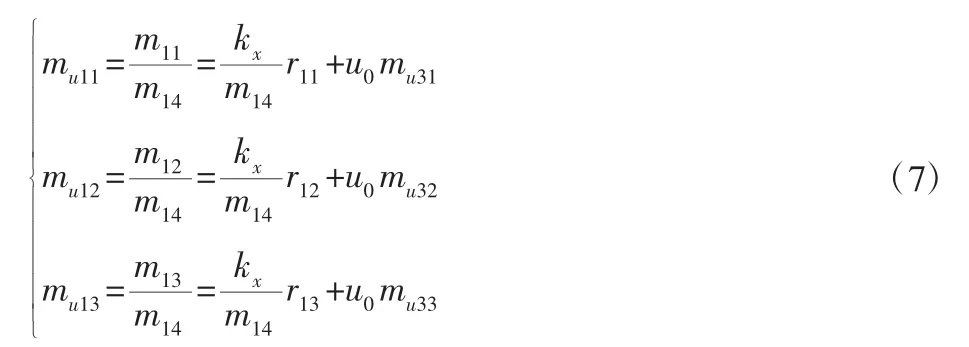
对式（4）的第二式两边同除以m24，得：Avmv=Bv。其中，

由式（6）与式（8）可知，

第四步，求解向量p。

由于m34即pz可由mu的相关参数解出，也可由mv解出，即pz=mu34（kxpx+u0pz）且 pz=mv34（kypy+v0pz）。

则：

根据pz初始值可求出px，py的初始值，代入上述方程组，建立超定方程组求最小二乘解对其进行优化即可得到px，py，pz的精确解。

4 实验结果比较

为了进行对比实验，选用三维棋盘格立体靶标。先后采用Matlab 标定工具箱（基于张正友标定法）、Faugeras 标定法、新的线性标定法进行标定。通过摄像机拍摄20 张图片，如图1所示。图像大小为640*480 个像素点，经过计算机测定得到角点坐标，每幅图像采集10 组角点（特征点）的图像像素坐标和世界坐标。

图1 标定图像Fig.1 Calibration Images

首先利用Matlab 标定工具箱即张正友标定法进行标定，得到内参数矩阵为：

对于新的线性方法，实验中选取主点坐标值为：u0=320/pixel，v0=240/pixel。对其使用VC 程序进行实现，具体界面，如图2 所示。利用Faugeras 方法与新的标定方法进行标定，选取其中5 组内参数结果，如表1 所示。

图2 新的线性标定方法程序实现界面Fig.2 Program Interface of the New Linear Calibration Method

表1 内部参数结果比较Tab.1 Comparison of Internal Parameter Results

由所采集的标定图像中选取一幅图像对外参数进行对比，张正友标定法得到的外部参数为：

Faugeras 标定法得到的外部参数为：

新方法得到的外部参数为：

解得摄像机全部参数之后，利用所求参数根据式（1），反推像素点的坐标值，并将平均像素误差作为判别标定结果精度高低的一个标准。

平均像素误差[9]为：

式中：（ui，vi）—像素点坐标的实际值—用实际三维世界坐标点推算出的坐标值；N—选取角点的个数。

平均像素误差Δr¯的值越小[10]，则表明所得结果越好，误差越小。经计算，对于20 幅图像，Faugeras 标定法的平均像素误差为13.5586mm，改进方法的平均像素误差为4.8386mm，结果表明，新的线性方法的精度高于传统的Faugeras 标定法。根据上述实验结果，可发现利用新的线性方法标定出的参数与张正友标定的结果更加接近。另外从表1 可发现Faugeras 方法标定出的图像中心点u0，v0有时偏差较大，显然不符合实际在（320，240）附近的情况。而新方法这种假设与实际情况更符合，其也带来其它标定参数精度的提高。但是新的线性方法标定所得的内参数对于个别图像具有偶然性，建议以多幅图像进行标定，再对最终结果进行迭代优化。提出的新方法，未考虑畸变以及未采用优化算法，便已得到了较高精度，为以后获得更高精度奠定了良好的基础。

5 结论

传统的Faugeras 标定对于摄像机标定模型只当成一般数学问题求解，并且将不同数量级的参数混合在一起形成关键参数m向量，同时采用从M 矩阵中分解出参数的方法，并未将变量间的约束关系考虑在其中，导致误差一级级增大。而当前诸多摄像机标定方法没有在线性标定阶段进行改善。针对该问题，提出了一种改进的线性标定法。该方法将参数分开求解，操作简便，相较于Faugeras 方法标定精度得到了提高。新方法即由研究人员自己编程实现，与Faugeras 的实现过程类似，实现比较简单，且可在视频中随时得到标定参数，便于今后用户自行开发可用于实时场合的完整标定软件。集中研究线性标定方法的改进，今后将进一步研究在新方法中考虑镜头畸变以及优化，有望得到更精确的解。