永磁同步电机定子振动特性分析

2020-08-17路文开

机械设计与制造 2020年8期

路文开，张卫，唐杨

（1.贵州大学，贵州贵阳 550025；2.贵州航天林泉电机有限公司，贵州贵阳 550003；3.国家精密微特电机工程技术研究中心，贵州贵阳 550003）

1 引言

国防装备、医疗器械和办公家电等领域用的永磁同步电机对振动提出较高的要求[1-3]。振动对电机的影响较大，它加速轴承的磨损，降低寿命，影响电机输出性能[4]。电机振动产生的噪声污染环境，影响人们生活[5]。因此在设计阶段避免电机共振，对电机振动特性分析尤为重要。

文献[1-2]建立永磁同步电机径向电磁力波解析式，分析径向电磁力对永磁电机电磁振动影响规律，并采用有限元法与试验法验证径向电磁力模型计算结果；文献[6-7]对比永磁电机径向电磁力谐波频率与定子铁心固有频率，进而判断电机振动情况，但忽略了绕组、机壳对铁心模态频率影响；文献[8]采用有限元法计算电机定子电磁力与结构频率，进而通过半解析方法判断电机电磁振动，该方法适用于简单定子结构；文献[9]采用试验方法对电机施加电磁脉冲得到电机电磁振动频率，进而通过机械结构模态试验得到电机固有频率，两者频率进行对比判断电机共振情况，试验方法较为可靠，但该方法较为繁琐，不便于设计初期阶段预测电机电磁振动。

综合上述文献研究基础上，以某永磁同步电机为研究对象，采用有限元计算方法得到了电机低阶电磁力频率与定子结构模态频率，进一步分析了电机振动特性，最后通过试验验证了模态分析合理性，为设计低振动永磁电机提供了依据。

2 数学模型

2.1 径向电磁力理论计算

采用永磁电机等效磁路法计算电机的气隙磁密，则永磁同步电机的磁密为[6]：

式中：f（θ，t）—气隙合成电动势；λ（θ，t）—气隙磁导。

永磁电机径向电磁力是产生振动与噪声主要原因之一，根据麦克斯韦张量法，电机气隙中的任意一点所受的电磁力可以表达为[6]：

式中：Pr（θ，t）—径向电磁力；（θ，t）—气隙磁密径向分量；μ0—空气磁导率。

由式（2）可以看出，永磁电机气隙磁密直接决定电机径向电磁力大小，因此可通过气隙磁密分布判断电机振动情况。

2.2 定子结构模态理论分析

在对永磁同步电机定子进行模态分析时，可以将定子作为一个线性的自由振动系统。其运动方程为[10]：

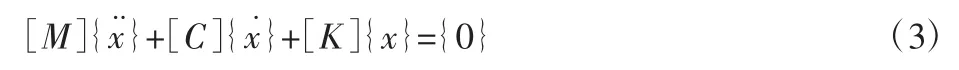
式中：［M］、［C］、［K］—定子质量、阻尼及刚度系数矩阵；—加速度、速度及位移矩阵。

永磁电机定子结构无阻尼时，定子的运动微分方程表示为：

方程的解可以表示为：

将得到通解代入方程（2）可得：

式（6）中方程的数值及特征值位移向量分别对应永磁电机定子固有频率、模态振型。

3 电机定子有限元模型

分析的永磁同步电机采用36 槽6 极，根据电机结构对称的特点，可以将有限元数值求解模型转化为二维半圆周，求解域截面结构，如图1 所示。

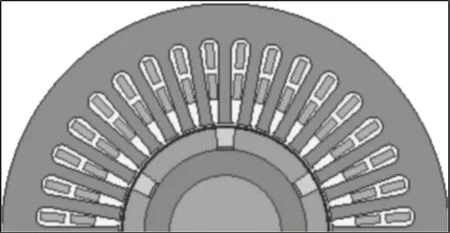
图1 电机结构Fig.1 The Structure of Motor

电机的定子主要有铁心、绕组、机壳等组成，根据电机实际物理模型结构，在不影响机械结构模态前提下，对电机定子系统结构进行适当的等效[11]，等效后定子模型，如图2 所示。各部件材料参数，如表1 所示。

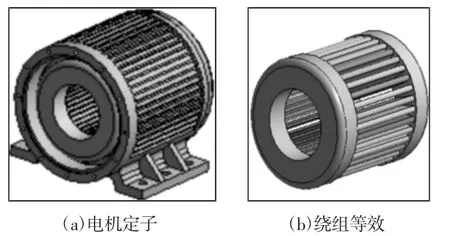
图2 电机定子有限元模型Fig.2 The Finite Element Model of Motor Stator

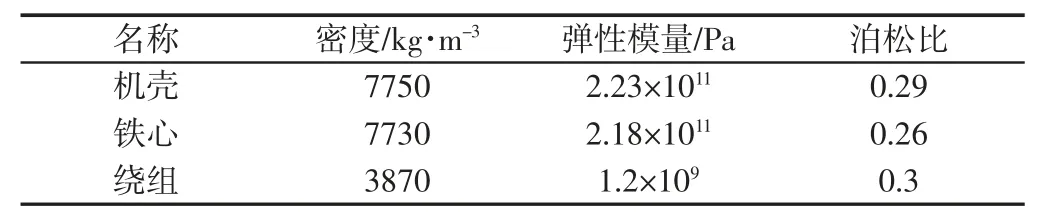
表1 各部件材料属性Tab.1 Material Properties of Parts

4 有限元计算结果与分析

4.1 电磁场计算与分析

在建立二维有限元模型基础上，采用有限元数值计算得到电机气隙磁场分布，进而判断电机的电磁力波对电机振动影响。采用有限元数值计算得到电机空载气隙磁密分布，如图3 所示。

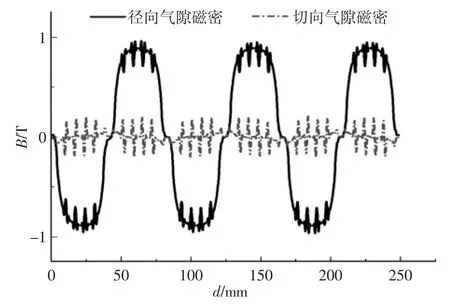
图3 切向、径向气隙磁密Fig.3 The Distribution of Air Gap Magnetic Density

图3 中径向气隙磁密接近于正弦，其幅值为0.97T；与径向气隙磁密相比，切向气隙气隙磁密幅值较小，幅值仅为0.21T，由此看出切向气隙磁密导致电磁力较小，其影响基本可以忽略不计。根据电磁力式（2）将径向气隙磁密产生电磁力进行求解，得到径向电磁力密度分布，如图4 所示。将径向电磁力曲线数据导入到数学工具Matlab 中进行傅里叶分解[12]，计算得到各阶谐波频率、幅值，如表2 所示。

图4 径向电磁力分布Fig.4 The Distribution of Radial Electromagnetic Force

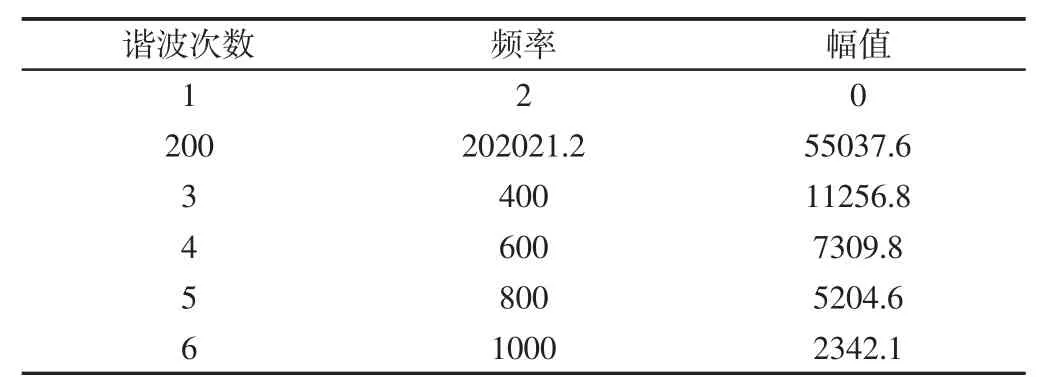
表2 电磁力谐波频率及幅值Tab.2 Harmonic Frequency and Amplitude of Electromagnetic Force

由表2 可得，电机在空载时2 次、3 次电磁力谐波易造成电机电磁振动，为了避免电机共振，在结构设计时，应避免2 次、3次电磁力谐波与电机定子固有结构模态频率接近。

4.2 固有频率计算与分析

在模态有限元数学理论和建立电机定子三维结构模型的基础上，采用有限元分析软件设置定子表1 中材料参数，划分网格、添加机座螺栓固定的边界条件，最后对电机定子进行模态求解[12]。计算固有频率、振型结果，如表3、图5 所示。

表3 有限元分析结果Tab.3 Finite Element Analysis Results

图5 有限元模态振型Fig.5 The Mode Shaps of Finite Element Mode

4.3 电机定子振动分析

当电磁力波频率与电机结构模态频率相近时，电机振动幅度增大，造成电机振动与噪声[5]。由表2、表3 可以看出定子结构2阶模态、频率819.38Hz 可能会产生共振，但该频率与5 次力波频率相差较远且力波幅值很小，其它次定子力波频率大于结构模态共振频率5%范围，表明电机定子结构设计合理。

5 电机定子模态试验验证

5.1 搭建试验平台

为了验证有限元模态分析可靠性，采用锤击法对永磁电机定子进行模态试验。为了保证信号采集仪“Sirius/DEWE-43”采集电机定子自由模态频率，将电机定子放置在弹性泡沫板上。试验方式选择为多点激励单点输出，在定子机壳外表面中间部位沿周向位置选取6 个激振点，采用“PCB 086C03”力锤垂直与机壳对各激振点敲击，敲击力信号尽量接近脉冲信号[13]。定子机壳外的“PCB 352C33”加速度传感器采集信号，然后通过“DEWEsoft v7.0”软件中频响函数计算、处理，最后在软件平台上显示，如图6所示。