飞机机电系统关键部件性能趋势分析方法

崔建国 ，徐昕明 ，于明月 ，蒋丽英

（1.沈阳航空航天大学自动化学院，辽宁 沈阳 110136；2.航空工业上海航空测控技术研究所故障诊断与健康管理技术航空科技重点实验室，上海 201601）

1 引言

飞机发电机是一类高度复杂的典型多部件电力机械系统，长期在恶劣环境中循环工作所产生的任何性能变化都可能对飞机造成严重灾难。其性能主要由某些参数所表征，一旦这些参数值发生异常，其性能就可能出现异常[1-2]。因此，寻找一种性能趋势预测方法是飞机发电机性能趋势分析研究重点。

目前，飞机发电机的性能趋势分析技术研究在近年来已成为国内外航空领域的研究热点之一，预测模型和算法是趋势分析技术的重要工具。但目前的一些预测算法仍存在许多问题，难以应用到工程实际中。如人工神经网络对数据信息量的要求较高，网络结构的确定比较困难，而LSSVM 则是容易造成局部极小值致使通过建立的模型得不到全局最优解，且学习算法还有待改进，难以适用于工程实践[3-5]。

组合预测的基本思路是把不同的预测模型组合起来，综合利用多种模型的特点和优势，改善预测的精确度和可靠性[6]。因此，提出了多项式趋势模型与ARMA 模型的组合预测方法，并将该方法应用于飞机发电机性能趋势的预测和分析，通过试验验证证明了该方法提高了预测精度，与以往方法相比具有更好的效果，且适合工程应用。

2 相关理论模型

2.1 多项式趋势预测模型

多项式趋势预测模型在数理统计中是一种将数据通过数学的方法来建立一个多项式模型。在许多工程实际问题中，可以通过采样等方法获取一定量的数据，由这些数据建立一个连续函数，并尽可能与获取的原始数据构成的曲线相吻合。

假设在时刻t0，t1，L，tn-1采集到的飞机发电机参数数据分别为x0，x1，L，xn-1，则该参数数据的多项式趋势预测模型为：

式中：a0，a1，L，am—多项式的趋势系数；m—多项式的阶次；ei—多项式趋势预测模型的误差。

在多项式趋势预测模型建立过程中，多项式的阶次值可通过观察模型的趋势拟合精度进行调整，工程应用中可根据实际的精度要求，来确定适当的值。

2.2 ARMA 模型

时间序列模型的创建是在线性模型基础上，以参数化的形式处理随机动态数据的一种比较实用方法。其特点是无需提前假定数据存在着一定的结构或模型，而是从数据本身出发，来寻找可以较好描述数据趋势的模型，从而保证创建的模型与更好地拟合原始样本序列的趋势，便于进行数理统计方面分析和处理[7]。由于ARMA 模型由自由回归AR（p）模型和移动平均MA（q）模型合并而成，所以记为 ARMA（p，q），表示如下：

式中：参数φj（1≤i≤p）—自由回归系数；参数θj（1≤j≤q）—移动平均系数；｛at｝—白噪声。式（2）可称为 p 阶自由回归 q 阶移动平均模型。

若引入一个后移算子B，式（2）可表示为：

其中，φ（B）=1-φ1B-L-φnBp；θ（B）=1-θ1B-L-θnBq。

构建ARMA 模型时，首先需要将随时间变化的样本序列进行平稳化处理，然后以对自相关系数和偏自相关系数的分析为基础，采用AIC 规则对所创建的ARMA 模型进行模型的阶数的确定，即确定p 和q 的值。在此基础上，通常使用非线性最小二乘的方法对模型中的参数φi和参数θj进行估计，也可以使用MATLAB工具箱中的Armax 函数实现。最后，采用拉格朗日乘数（Lagrange multiplier）对所创建的模型进行随机检验，即检验模型的残差序列是否为白噪声。一般来说，如果检验概率大于0.05 时，则该残差序列为白噪声。

2.3 组合预测模型

组合预测是对某一科学或工程实际应用的问题，将两种或两种以上不同的模型进行适当地组合，综合利用多种不同模型所提供的信息及其特点和优势，改善预测的精度。将多项式趋势预测模型和ARMA 模型进行组合，如图1 所示。

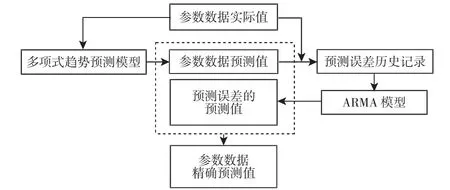
图1 组合预测过程Fig.1 Combination Prediction Flow

通过获取的参数数据实际值，建立多项式趋势预测模型，得到预测值和每个预测值与实际值的误差历史记录。以此作为样本建立ARMA 模型，使用该模型来对多项式趋势预测模型的预测误差进行预测，再将得到预测误差值与多项式趋势模型所得预测值进行相加，即可得到更为精确的预测值。

3 性能趋势分析试验

采用多项式趋势预测模型与ARMA 模型的组合预测对飞机发电机的性能趋势进行试验和分析，通过专用试验平台中的传感器和数据采集系统来获取某型飞机发电机的特征参数如转速、负载、注油压力、电压等大量原始样本数据。深入分析所采集的试验参数数据并结合工程经验可知，当注油压力值小于某一阈值（一般为0.8）时，飞机发电机的工作状态将会出现异常，性能将会迅速变差，可能直接影响到飞机的正常工作和运行。因此，以注油压力为飞机发电机的性能表征参数，对该型飞机发电机的性能趋势进行试验研究和分析。

首先，对所获取的试验数据进行预处理，排除掉干扰数据和无用数据，选择一部分时间关联性较强的数据作为试验研究数据，并将这些数据根据飞机发电机的转速进行分类，将同一转速下数据归为同一组，以此来保证进行试验的数据的有效性。在整个试验的过程中，共获取了40 组连续时间内获取的注油压力（MPa）原始数据，每组有30 个数据，组成一组原始样本序列，如：｛1.97，1.96，L，0.97，0.91｝。以该组原始序列为例进行飞机发电机性能趋势分析研究试验。

3.1 多项式趋势预测试验验证

通过调整趋势拟合精度，选定多项式趋势预测模型的阶数为3，利用监测到的注油压力原始数据序列中的前20 个数据样本点建立多项式趋势预测模型，通过所建立的模型对接下来10个数据样本点的进行预测，将得到的原始数据样本点与预测值分别连成曲线，即可得出飞机发电机在某一段时间内实际和预测的性能变化趋势。将得到的预测值序列组成的预测趋势与原始数据值序列组成的实际趋势作对比可得到多项式趋势预测模型的预测效果，如图2 所示。

图2 多项式趋势模型的预测效果Fig.2 Polynomial Trend Prediction Model Prediction Effect

将原始序列与多项式趋势预测模型得到的预测序列作差即可得到多项式趋势预测模型的预测误差序列，如图3 所示。

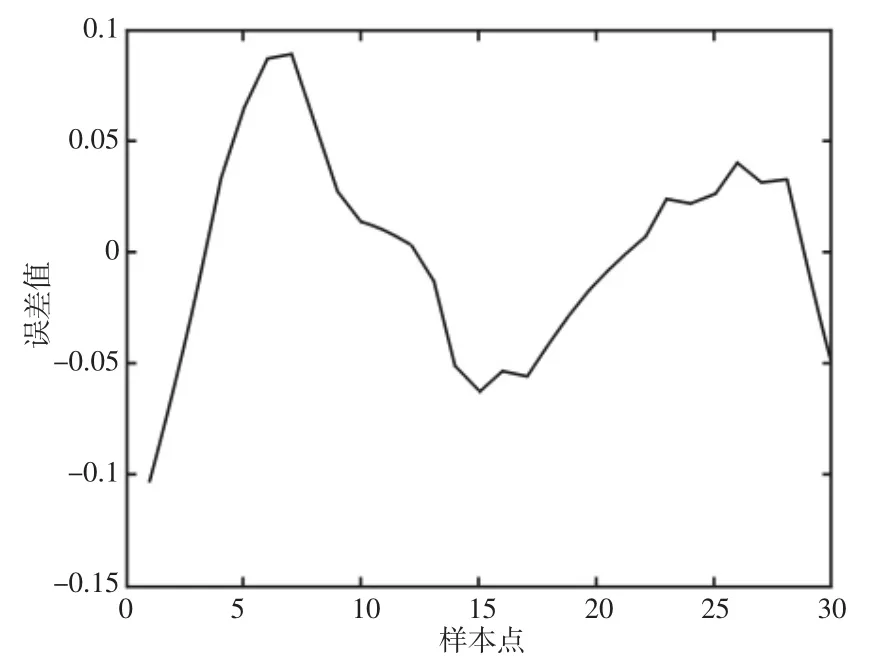
图3 多项式趋势预测模型的预测误差序列Fig.3 Predictive Error Sequence of Polynomial Trend Prediction Model

3.2 基于ARMA 模型的误差值预测

在3.1 节基础上，得到了多项式趋势预测的30 个误差值。使前20 个误差值作为样本来建立ARMA 模型，用后10 个误差值检验ARMA 模型误差值预测的效果。首先，使用AIC 规则对ARMA模型进行模型的阶数的确定。通常情况下，ARMA 模型的阶数p和q 数值变化区间不大，所以假设p 值的变化范围为（2～6），q值的变化范围为（4～8）（p 和q 值的变化范围也可据实际情况调整）。通过借助统计类专用软件的多次迭代计算可以计算出多个ARMA（p，q）模型 AIC 估计值，比较这些 AIC 值可得到一个最小AIC 值为-5.2312，并且以此可以确定这个最小AIC 值所对应阶数组合为（p，q）=（3，7）。通过 Armax 函数工具箱对 ARMA（）模型进行参数估计，结果如下：

综合式（3）、式（4）和式（5）即可得到 ARMA 模型，运用该模型对多项式趋势预测误差值进行预测，误差预测效果，如图4 所示。从图4 中可知，ARMA 模型可以较为准确地预测多项式趋势预测模型对参数的预测误差。

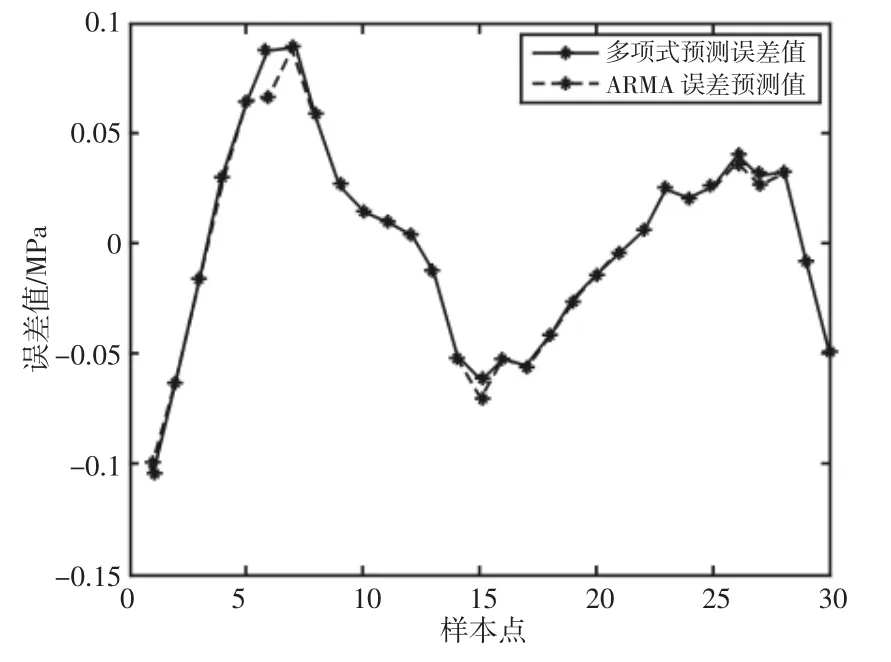
图4 ARMA 模型的误差预测效果Fig.4 Error Prediction Effect of ARMA Model

3.3 组合预测试验验证

根据组合预测原理（如图1）并结合3.1 节与3.2 节的实验结果，假设多项式趋势预测模型的预测值为y，ARMA 模型预测到多项式趋势预测模型对参数的预测误差值为ε，则组合预测的预测结果 Y 为：

依据式（6），可得到更为精确的飞机发电机注油压力趋势预测值序列并与注油压力原始数据值对比，如图5 所示。将组合预测的效果，与多项式趋势预测模型和ARMA 模型的预测的效果进行对比，如图6 所示。

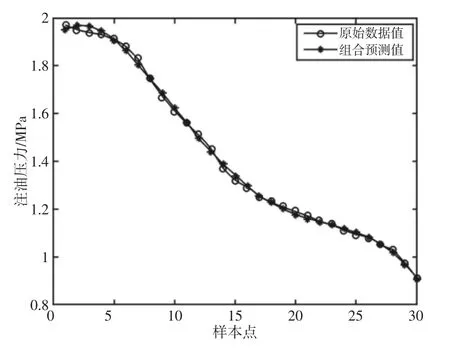
图5 组合预测效果Fig.5 Combination Prediction Effect

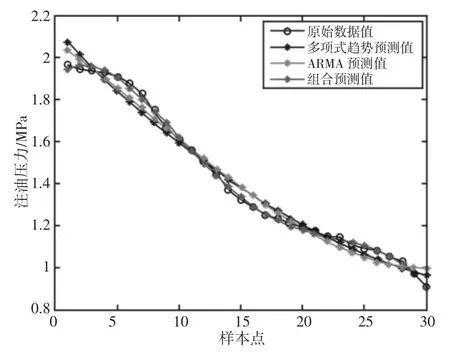
图6 三种方法预测效果的比较Fig.6 Comparison of Three Methods for Predicting Results

以均方误差（Mean Square Error，MSE）值大小作为预测效果的评判标准，分别计算三种模型的MSE 值，如表1 所示。从图2、图5 和图6 中的趋势预测结果可知，注油压力值将会在未来的一段时间内仍保持下降趋势甚至低于0.8。所以，随着时间的推移，该型飞机发电机性能会逐渐变差，很可能会发生故障并影响飞机的飞行安全。结合图6 和表1 可知组合预测的方法要比以往预测模型的预测MSE 值更小，因此组合预测在飞机发电机性能趋势分析的研究和应用中效果更好。

表1 三种方法的均方误差计算结果Tab.1 Mean Square Error Results for Three Methods

4 结论

提出了一种将多项式趋势预测模型和ARMA 模型进行适当组合的预测方法，充分利用了多项式趋势预测模型良好的拟合能力和ARMA 模型的时间序列分析功能，并将该方法应用于飞机发电机性能趋势分析研究。经过试验验证表明，这种组合预测方法的预测效果要好于以往的预测模型，具有较高的工程应用价值和广泛的应用前景，更适用于飞机发电机性能趋势分析研究，进而更好保证飞机的安全运行。