GH4169 合金高温变形过程本构方程

吴 昊，孔祥伟，罗 平

（1.辽宁科技大学工程训练中心，辽宁 鞍山 114051；2.东北大学机械工程与自动化学院，辽宁 沈阳 110819；3.楚天科技股份有限公司 技术研发中心，湖南 长沙 410600）

1 引言

GH4169 合金是一种镍基高温合金，其化学组成成分与Inconel 718 合金相似。由于具有高强度、良好的延展性，优异的抗氧化性、耐腐蚀性及机械性能，该合金广泛应用于航空航天，石油，化工，核能等领域[1-5]。近年来，随着对航空发动机叶片，涡轮盘等关键性零件的制造精度要求的提高，加工工艺制定和产品质量控制[6]受到高度重视。在GH4169 合金的塑性加工过程中，本构方程是塑性变形的基础，为工艺参数的确定提供依据。因此，建立预测精度较高的本构方程成为首要任务。目前，研究人员做了大量的工作研究合金的热变形过程本构方程和热变形行为。文献[7]研究δ 相实效态GH4169 合金在一定的变形温度、应变速率条件下的热变形行为，不仅建立该合金热变形本构方程，而且分析不同应变量下的热加工图并对预测结果进行分析。文献[8]利用高温压缩试验，得到DP 工艺处理的GH4169 合金在不同变形温度、应变速率下的高温本构模型，并对合金的显微组织进行了定量分析，得到预测值与试验值吻合较好。文献[9]在不同变形温度、应变速率、变形量的条件下，利用热模拟机对GH4169 合金进行压缩试验，建立该合金的本构方程并分析变形条件对合金微观组织的影响。文献[10]研究了GH4169 合金变形条件对流变应力的影响，并建立基于双曲正弦模型Arrhenius 的本构方程，其中峰值应力的计算值与试验值的拟合程度较好。文献[11]采用等温压缩实验，研究了Inconel 718 合金不同变形条件下的热变形行为，并建立描述该合金热变形行为的本构方程。流变应力的预测值与实验结果的吻合程度较好，说明建立的模型能够准确反应该高温合金的热变形行为。文献[12]利用MTS 设备在不同变形条件下对Inconel 718 合金进行压缩实验，基于实验数据建立表现该合金热变形行为的数学模型，并分析热变形参数对流变应力和晶粒尺寸的影响。文献[13]建立了描述Inconel 718 合金热变形行为的本构模型和晶粒尺寸模型，该模型可应用在有限元分析，在热变形工艺（开坯或锻造）过程中，来预测流变应力和微观组织。因此，建立预测精度高的GH4169 本构方程在塑性变形数值模拟和工艺参数优化方面具有重要的意义。

2 实验材料及实验方法

2.1 实验材料

实验材料为GH4169 合金，其化学成分[14-15]，如表1 所示。利用数控线切割设备将GH4169 合金锻造棒料加工成φ（8×12）mm的圆柱体加工试样。对加工完的试样打磨、抛光处理后，进行化学腐蚀。在显微镜下观察其初始微观组织，如图1（a）所示；经过热处理后的微观组织，如图1（b）所示。

表1 GH4169 合金化学成分Tab.1 Chemical Composition of GH4169 Alloy

图1 GH4169 合金微观组织Fig.1 The Microstructure of GH4169 Alloy

2.2 实验方法

将处理后的试样以10℃/s 的速率分别加热到不同变形温度下，保温3min 确保其内外温差一致，以不同的变形速率对试样进行压缩实验，压下率为50%。压缩结束后，利用水淬的方法对试样进行冷却，热模拟工艺，如图2 所示。

图2 热模拟压缩实验工艺Fig.2 Thermal Simulation Compression Experiment Process

3 实验结果与分析

3.1 实验结果

在（950～1100）℃变形温度下，（0.01～10）mm/s 变形速率下，压下率为50%的GH4169 合金热模拟压缩实验后的真应力-真应变曲线，如图3 所示。

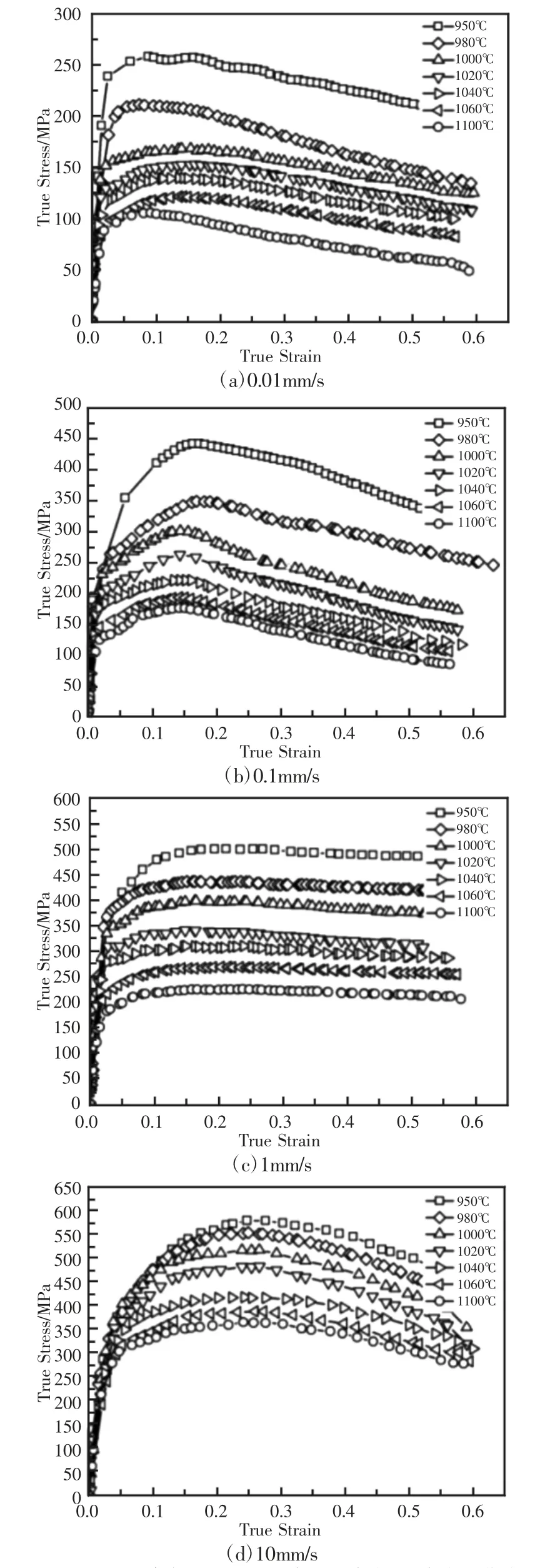
图3 不同变形条件下GH4169 合金的真应力-真应变曲线Fig.3 True Stress-Strain Curves of GH4169 at Different Deformation Conditions

3.2 变形参数影响分析

3.2.1 变形温度的影响

由图3（a）可知，如果变形速率恒定时，当变形温度升高时，GH4169 合金的流变应力减小。主要原因是温度升高时，金属原子的运动速度和频率增加，原子间的相互作用力变弱，而且可能会增加并启动新的滑移系[16]，这将导致临界切应力降低；同时较高的温度有利于晶核生长[14]，又进一步加快动态再结晶，消除变形过程中产生的加工硬化。因此，温度越高，完成动态再结晶过程的时间越短，对GH4169 合金的软化效果增强，塑性变形也更容易发生。

3.2.2 变形速率的影响

由图3（a）、图3（b）对比可知，如果变形温度恒定时，当变形速率增加时，该合金的流变应力也随之增大。由于变形速率增加，完成塑形变形的时间相对减短，在变形过程中位错运动的发生与发展时间不充分[14]，变形抗力也因此增加；另一方面变形速率的快慢决定动态再结晶发生是否完全。较大的变形速率可能使该合金没有足够时间发生动态再结晶[17]，软化效果减弱，在变形过程中产生的加工硬化无法及时消除。故变形速率越大，GH4169 合金的流变应力增大，塑性也随之降低。

4 GH4169 合金高温本构方程建立

4.1 材料参数 n1、β、α 的求解

采用Arrhenius 形式的表达式[18-23]来建立GH4169 合金的高温本构方程，主要描述热变形中流变应力、应变速率和变形温度之间的关系，如式（1）、式（2）所示。

对式（1）、式（2）两侧分别取自然对数得：

不同变形温度下 lnσp、σp和 lnε˙之间的关系，如图4 所示。通过线性拟合，由图4（a）求出各条直线的斜率后，对各斜率取倒数并求出平均值，可得 n1=6.7310；同理，由图4（b）求出 β=0.02332，由于 α=β/n1=0.00346。

图4 ln˙与 lnσp 之间关系及 lnε 与 σp 之间关系Fig.4 The Relationship Between lnε and lnσp and the relationship Between lnε and σp

4.2 激活能Q 的求解

文献[18，20-21，23-24]提出可应用在所有流变应力情况下的关系式。利用该关系式可描述应变速率ε˙和流变应力σ、变形温度T 以及激活能Q 参数之间的关系，该关系式被称为修正的Arrhenius 关系式，如式（5）所示。

式中：Q—激活能（单位：kJ/mol）；R—理想气体常数，值为8.314（单位：kJ/（mol·K））；T—绝对温度（单位：K）；A、n—材料常数。

对式（5）两侧取自然对数得：

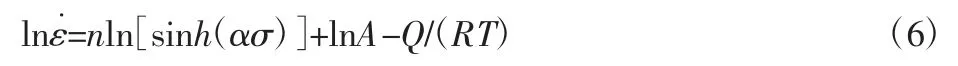
假设Q 与应变速率无关时，对式（6）两侧分别取1/T 的偏导数得：

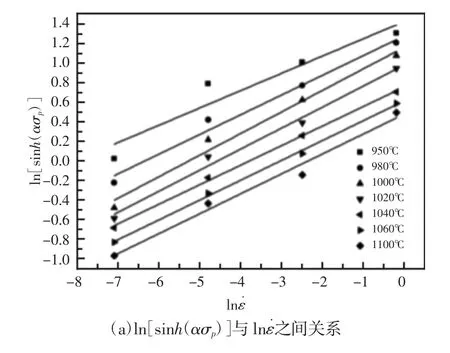
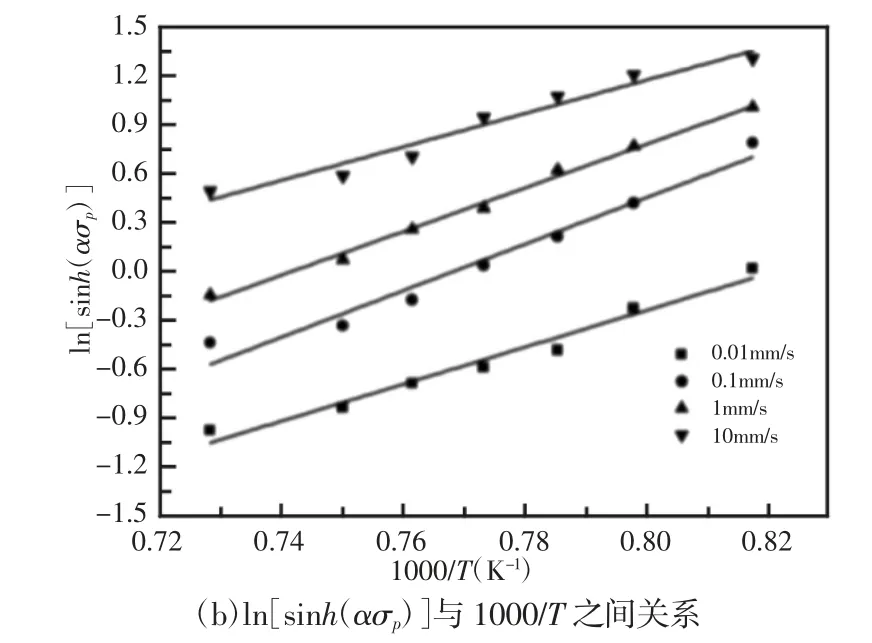
图5 ln［sinh（ασp）］与 ln˙之间关系及 ln［sinh（ασp）］与 1000/T 之间关系Fig.5 Relationship Between ln［sinh（ασp）］and lnε˙Relationship Between ln［sinh（ασp）］and 1000/T

4.3 材料参数A 的求解

文献[21，23，25-26]两位学者引入 Zener-Hollomon 参数来建立应变速率与变形温度和激活能之间的关系，该参数表达式，如式（9）所示。

将式（5）代入到式（9）中得到的关系式，如式（10）所示。

对式（10）两侧同时取自然对数，可得：

lnZ 与 ln［sinh（ασp）］之间关系，如图6 所示。通过线性拟合，该直线在lnZ 轴上的截距即为lnA 的值，求得材料常数A=2.46748×1018。

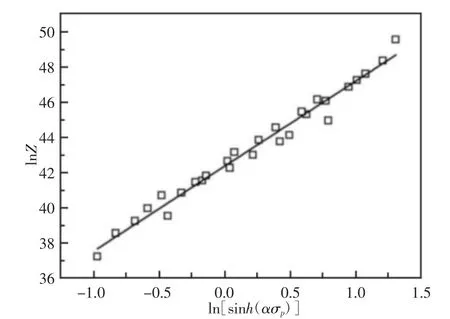
图6 lnZ 与 ln［sinh（σp）］的关系Fig.6 Relationship Between lnZ and ln［sinh（σp）］

在变形温度为 950℃、980℃、1000℃、1020℃、1040℃、1060℃、1100℃，变形速率为 0.01mm/s、0.1mm/s、1mm/s、10mm/s 的情况下，GH4169 合金的高温本构方程的参数值，如表2 所示。

表2 本构方程参数值Tab.2 The Value of Parameters for Constitutive Equation

综上所述，建立GH4169 合金的高温本构方程为：

5 GH4169 合金本构方程准确性的验证

为了验证GH4169 合金流变应力方程的预测精度，需要计算在不同热变形参数下的峰值应力值，将预测值与实验采集得到的峰值应力作比较。

根据线性相关系数（R）和平均相对误差（AARE）来验证GH4169 合金高温本构方程的预测精度[21，26]。其表达式，如式（12）、式（13）所示。

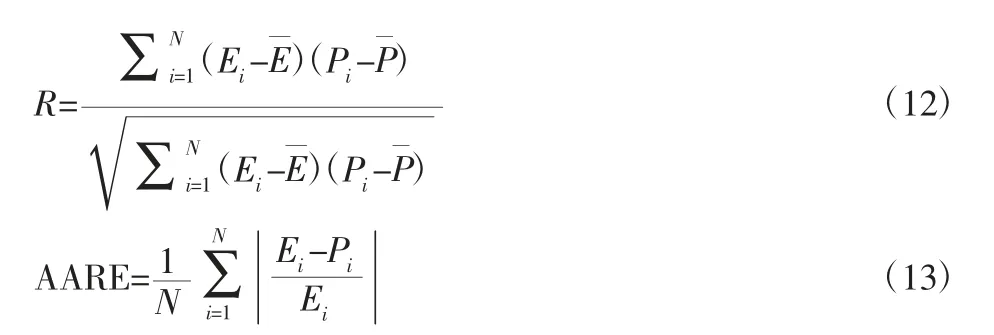
不同热变形参数下的峰值应力实验值与预测值，如表3 所示。线性相关度为0.977，表明预测值与实验值吻合程度良好，计算结果平均相对误差约为5.13%，也验证了GH4169 合金的流变应力方程有较高的预测精度，比较结果，如图7 所示。

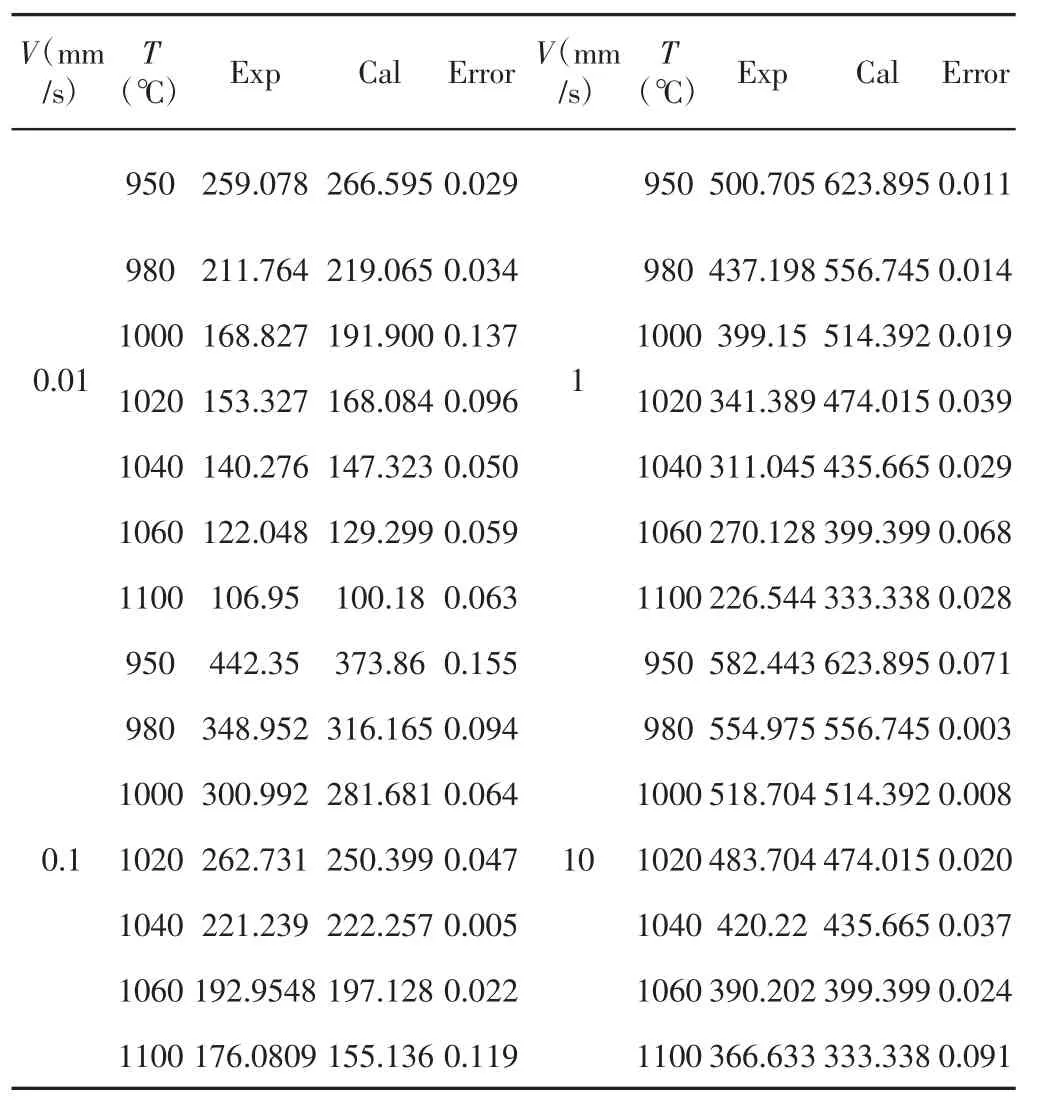
表3 GH4169 合金的流变应力实验值和预测值比较Tab.3 Comparison of Experimental and Predicted Values of GH4169 Flow Stress

图7 预测值与实验值和相关性比较Fig.7 The Predicted Values of Comparing with Experimentsand Correlation

6 结论

（1）通过分析热变形参数GH4169 合金流变应力的影响。得到以下结论：与大部分的金属材料热变形规律相同，如果变形速率恒定时，当变形温度升高时，其流变应力随之减小；如果变形温度恒定时，当变形速率增大时，其流变应力也随之增大。

（2）利用线性回归的方法，在不同的热变形参数下，建立GH-4169 合金的Arrhenius 双曲正弦形式高温变形过程本构方程为：

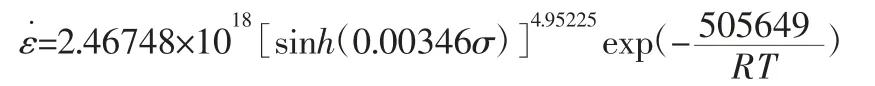
（3）将上述本构方程预测的峰值应力与实验所采集的峰值应力相比较，平均相对误差为5.13%，线性相关度为0.977，表明建立的本构方程具有较高的预测精度，对GH4169 合金在塑性变形数值模拟和工艺参数优化方面具有指导意义。