概率行为树模型转化为模型检测模型方法研究

侯 翌，杨培林，徐 凯

（西安交通大学机械工程学院，陕西 西安 710049）

1 引言

由于机电系统的功能与结构日趋复杂，其可靠性问题日显突出，可靠性已成为衡量机电系统性能的重要指标之一。

为了提高机电系统可靠性分析特别是FMEA 分析的准确性与效率，近年来有学者对基于模型检测的机电系统可靠性评价进行了研究[1-6]。基于模型检测对机电系统进行可靠性评价时首先要建立系统的形式化模型，然后借助模型检测工具（Model Checker）自动遍历系统的形式化模型（形式化验证）进而实现可靠性评价，因此能有效提高可靠性分析特别是FMEA 分析的准确性与效率。用模型检测工具提供的建模语言进行形式化建模难度较大，为了使机电系统的形式化建模过程更加直观并降低建模难度，通常采用图形化的建模方法进行形式化建模，然后再将其转化为模型检测工具所能接受的形式化模型（模型检测形式化模型，即利用模型检测工具提供的建模语言建立的模型），以便于后续的形式化验证和可靠性评价。

概率行为树PBT（Probabilistic Behavior trees）作为一种图形化建模方法[7-13]，具有严格的形式化语义和图形句法，其建模思路接近系统的需求模型和设计模型，具有良好的层次特性并易于维护，因此特别适合复杂机电系统的形式化建模。以利用概率模型检测工具PRISM[14]（Probabilistic Symbolic Model Checker）对机电系统进行可靠性评价为背景，首先对机电系统的概率行为树建模进行了介绍，分析了概率模型检测工具PRISM 提供的形式化建模语言，然后定义了从行为树模型到PRISM形式化模型的转换规则，实现了机电系统行为树模型向模型检测形式化模型的转换，为进一步利用概率模型检测工具PRISM 进行可靠性评价提供了便利。

2 概率行为树与机电系统的概率行为树建模

2.1 概率行为树

概率行为树 PBT 由节点（Nodes）和箭头（Arrows）组成[8]。每个节点与系统的一个组件（component）相关联。节点的类型包括：状态实现节点、输入输出节点、条件节点、守卫节点和原子节点等。箭头表示控制流，它规定了节点信息的传递方向。行为树有三种控制流，分别为：顺序流、选择流和并发流。较复杂的概率行为树可由若干子行为树构成。

行为树节点的标签（Label）指定了控制流的流动方向。带有标签的节点称为原始节点，目标节点指行为树中与原始节点有同样名称和行为的节点。不同的标签具有不同的含义，其中常用的为回溯标签“^”，如图1 所示。它表示控制流由原始节点跳回到目标节点。

图1 节点标签Fig.1 Node Label

2.2 机电系统的概率行为树建模

基于概率行为树的语义和特征，可用概率行为树描述机电系统的行为过程，实现对机电系统的概率行为树建模。机电系统概率行为树模型中的节点主要包括以下几种。

2.2.1 状态实现节点

状态实现节点表达了机电系统功能载体变迁过程中所处的某种状态。例如某传感器处于高电平状态，则可用节点表示，如图2 所示。

图2 状态实现节点Fig.2 State Realization Node

2.2.2 输入输出节点

输入输出节点表达各功能载体发生同步状态变迁时的信息交流，如图3 所示。输出节点表示功能载体“电机”发出信息“电机启动”；输入节点表示功能载体“滚珠丝杠”接受信息“电机启动”。这时，在信息“电机启动”驱动下，电机与滚珠丝杠实现同步运动。

图3 输出输入节点Fig.3 Output and Input Node

2.2.3 守卫节点

守卫节点描述机电系统功能载体发生变迁的使能条件（事件）。守卫节点中的概率信息λ 表示该守卫节点前后状态实现节点之间的状态变迁率。例如某传感器从“正常”状态向“失效”状态变迁时，其对应的守卫节点，如图4 所示。图中：λ—传感器的失效率。

图4 守卫节点Fig.4 Guard Node

2.2.4 原子节点

原子节点用于表示机电系统功能载体的多状态并发，原子节点中的状态实现节点之间用短竖线（|）连接。例如电机在满足“启动电机”这一变迁条件时，同时发出“启动运行”的信号，这两个行为可用原子节点表示，如图5 所示。

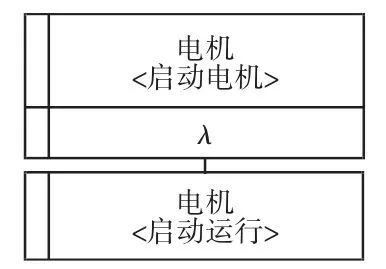
图5 原子节点Fig.5 Atomic Node

3 模型检测工具PRISM 及其形式化建模语言

概率模型检测工具PRISM 一种广泛使用的概率模型检测工具，它支持多种概率模型，如连续时间马尔科夫链CTMC（Continuous Time Markov Chains）、马尔科夫决策 MDP（Markov Decision Processes）、概率时间自动机 PTA（Probabilistic Timed Automata）等，适用于复杂系统的概率模型检验[13]。

PRISM 建模语言由模块（Modules）和变量（Variables）两种基本元素组成。PRISM 形式化模型由一个或多个模块构成，各模块之间可以交互作用。模块由变量和命令组成，如图6 所示。图中：x—模块的变量，“［］x=0->0.6：（x′=1）”—模块中的命令。

图6 PRISM 模块Fig.6 PRISM Module

变量可以是局部变量（属于特定模块）也可以是全局变量（属于整个模型）。一个模块包含一个或多个局部变量，这些变量的值组成了模块的状态。比如电机有“关闭”和“启动”两个状态，PRISM 建模语言会将电机状态描述为：motor：［0..1］

其中motor 为变量，motor=0 代表电机处于关闭状态，motor=1 代表电机处于启动状态。

模块的行为（状态的变迁）通过命令（commands）来定义，命令由守卫（guard）和更新（update）组成，命令的组成形式为：

［］guard->prob_1：update_1+…prob_n：update_n

其中，守卫描述的是状态变迁执行需要满足的条件，即“事件”。守卫由模型的变量值（可以是该模块中的局部变量也可以是其他模块中的变量）描述，更新描述了变迁后的状态。当满足守卫时便可以执行相应的变迁，变迁的概率由prob_i 表示。当系统模型为CTMC 时，prob_i 表示的是状态变迁率。比如传感器有“正常”和“失效”两个状态，PRISM 语言描述为 sensor：［0..1］，0 代表“正常”，1 代表“失效”，则：［］sensor=0->λ：（sensor′=1）

表示传感器从正常状态向失效状态的变迁，状态变迁率为λ。

如果系统中两个或多个变迁同步发生，可以通过同步（synchronization）的方式实现对该种情况的描述，具体而言就是在命令前的方括号内加入同样的“标记”。此时，加入“标记”的命令同时执行，即发生同步变迁。

按照PRISM 语言规则，同步变迁率为参与同步变迁的各个变迁率的乘积。实际建模时，通常将一条同步变迁语句中的变迁率直接设定为同步变迁率，而把其他同步变迁语句中的变迁率设定为1。例如，电机（Motor）通过滚珠丝杠带动工作台（workbench）运动，电机正转时工作台前进，电机反转时工作台后退。当电机由正转变为反转，工作台则由前进变为后退。二者的变迁可以看作是同时发生的。描述该过程的PRISM 模型，如图7 所示。二者通过在命令前的方括号内加入标记“return”实现了变迁的同步，同步状态变迁率为Lambda。

图7 同步变迁Fig.7 Synchronization Transition

4 概率行为树模型到PRISM 模型的转换

4.1 转换规则

通过研究概率行为树与PRISM 建模语言的语义和句法，根据行为树模型与PRISM 形式化模型相关元素之间的对应关系，得到概率行为树模型与PRISM 形式化模型之间的转换规则如下。

转换规则1：行为树模型中功能载体名称转换为PRISM 模型中模块的名称和变量名，行为树模型中每个子行为树对应PRISM 模型中的一个模块。行为树模型中电机子行为树转换为PRISM 模型中的电机（Motor）模块，如图8 所示。工作台（Workbench）子行为树转换为PRISM 模型中的工作台模块。

图8 功能载体名称的转换Fig.8 Conversion of Functional Carrier Name

转换规则2：行为树模型中任意子行为树的状态实现节点数对应PRISM 模型中该模块的状态数，按照状态实现节点的出现顺序从（0～n）自动排序，且初始状态始终为“0”。其中，回溯节点与其目标节点为同一节点，不再参与排序。在出现并发流的情况下，分支从左到右依次排序。电机（Motor）子行为树共有三个状态实现节点，则PRISM 模型中电机模块则有三个状态，其中0 代表正转“forward”、1 代表反转“reverse”、2 代表关机“stop”，初始状态为“0”，如图9 所示。

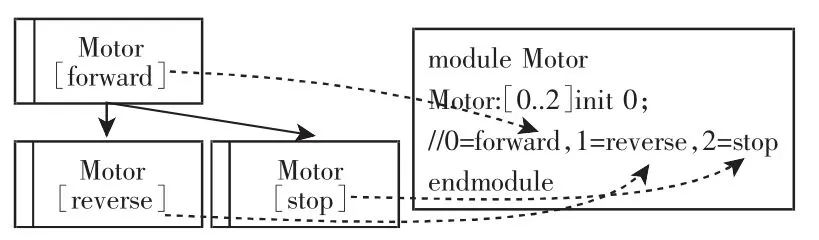
图9 状态实现节点的转换Fig.9 Conversion of State Realisation Node

转换规则3：行为树模型中两状态实现节点间的守卫节点转换为PRISM 模型中与之对应两状态间的变迁条件（守卫），守卫节点中的概率信息转换为状态变迁率，如图10 所示。

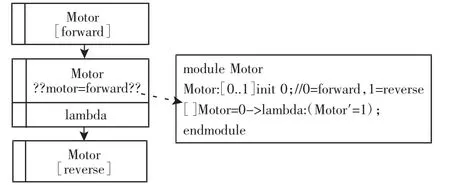
图10 守卫节点的转换Fig.10 Conversion of Guard Node

转换规则4：行为树模型中输入输出节点的信息转换为PRISM 模型中同步变迁命令语句前的同步标志。图中分别为工作台（Workbench）和传感器（Sensor）子行为树，传感器安装在工作台的前端（front），如图11 所示。当工作台离开前端时，便会发出信息“leave”，传感器收到此信息后由高电平状态（high）向低电平状态（low）变迁。输入输出节点中的信息“leave”转换为相应变迁语句前面的同步标志，表示两个状态变迁同步进行。

转换规则5：行为树模型中子行为树之间有信息通讯时（通过输入输出节点实现），PRISM 模型各模块间的同步变迁语句中只有输出节点对应的变迁语句具有变迁率，其余输入节点对应的变迁语句中的变迁率缺省（在PRISM 语句中变迁率缺省时默认为1）；子行为树之间无信息通讯时，PRISM 模型中变迁语句的变迁率则不能缺省。由于工作台子行为树中是输出节点，传感器子行为树中是输入节点，故PRISM 模型中只有工作台模块的同步变迁语句中有“1/60”的变迁率，传感器的同步变迁语句中的变迁率自动缺省，如图11 所示。

图11 输入输出节点的转换Fig.11 Conversion of Input and Output Node

4.2 建模工具开发

基于上述转换规则，利用C#开发了机电系统概率行为树建模工具 BTEditor（Behavior Trees Editor），如图12 所示。利用该建模工具不仅可以创建机电系统的概率行为树模型，还可以将该行为树模型自动转换为PRISM 代码（PRISM 形式化模型），为下一步利用模型检测工具PRISM 进行可靠性评估提供了方便。

图12 行为树建模工具BTEditorFig.12 Behavioral Tree Modeling Tools BTEditor

5 实例分析

以简化后的机床工作台系统为例。在该系统中，共有三个功能载体，分别是电机（Motor）、工作台（Workbench）和上极限位置传感器（Topsenor）。电机带动工作台在上极限位置和下极限位置间做往复运动。当电机正转时，工作台由上极限位置向下极限位置运动；当电机反转时，工作台由下极限位置向上极限位置运动。在工作台的上极限位置设有上极限位置传感器，当工作台到达上极限时，上极限位置传感器由低电平变为高电平，电机则会改变旋转方向；反之，当工作台离开上极限时，上极限位置传感器会由高电平变为低电平。工作台到达下极限位置时电机会自动改变旋转方向（实际上在下极限位置也设有极限位置传感器，为简化起见在此略去）。根据各功能载体的行为逻辑，分别建立了三个功能载体的子行为树，如图13 所示。

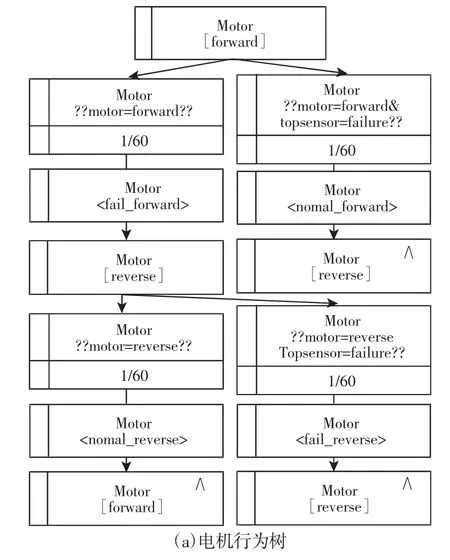
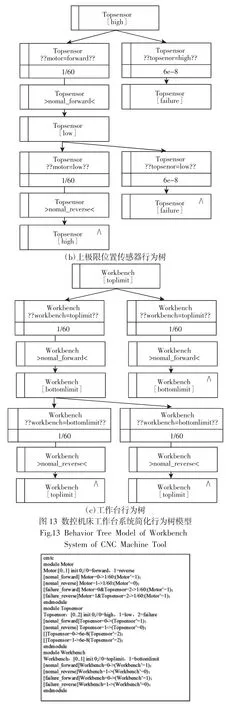
图14 数控机床工作台系统PRISM 模型Fig.14 PRISM Model of Workbench System of CNC Machine Tool

根据上述转换规则，将行为树模型转换为PRISM 形式化模型，如图14 所示。电机、上极限位置传感器与工作台三个功能载体分别对应PRISM 模型中的三个模块。各模块分别描述了三功能载体在上极限传感器正常和故障两种状态时的状态变迁。

6 结论

建立机电系统的形式化模型是利用概率模型检测工具对其进行可靠性评价的前提。根据机电系统概率行为树模型与PRISM 建模语言的语义和句法，给出了由概率行为树模型向模型检测工具PRISM 形式化模型转换的规则。利用转换规则，可直接从机电系统的概率行为树模型转换为模型检测形式化模型，避免了直接使用模型检测语言建模带来的困难，为基于概率模型检测的机电系统可靠性评价提供了方便。