齿面微观几何形貌对齿轮啮合振动影响的研究

申传鹏，阿达依·谢尔亚孜旦，王晓岗

（新疆大学机械工程学院，新疆 乌鲁木齐 830047）

1 引言

良好的振动特性是评价齿轮传动性能的重要指标，因此，国内外相关学者结合机械振动学、非线性振动与随机振动理论、小波振动建模与识别以及振动主动控制等领域取得的研究成果[1-4]，改善了齿轮传动的振动性能[5-6]。但值得关注的是，这些研究并未涉及到加工方法对齿轮啮合振动性能的影响。相关实验结果表明，与剃齿齿面相比，经电化学光整加工处理后的齿轮的啮合噪音平均降低了7.8 分贝[7]。这表明，加工方法影响齿轮传动的啮合噪音。由于啮合噪音的降低实际上反映了齿轮啮合振动特性的改善，因此，加工方法影响齿轮啮合的振动特性。

实际上，受材料物理特性以及加工工艺系统等的影响，轮齿齿面的表面微观几何形貌呈不平状，且加工方法不同，齿面微观几何形貌也存在显著差异。由于齿面微观几何形貌受啮合过程中外载荷的作用而产生弹、塑性变形，并以应变能的形式存储和耗散外部激励能，具有明显的阻尼特性，因此，齿面微观几何形貌的差异，从一侧面反映了齿轮接触阻尼特性的差异，也就是说，齿面微观几何形貌影响齿面接触的阻尼特性。

虽然许多学者从齿轮啮合刚度及其啮合阻尼等方面对齿轮传动的振动特性进行了相关研究[8-10]，但是这些研究基本上建立在齿面绝对光滑的假设基础上，且以刚度的周期时变性及齿轮传动时产生的润滑油膜阻尼为主要研究内容，并未涉及到齿面微观几何形貌产生的阻尼特性对齿轮啮合振动性能的影响。因此，就齿面微观几何形貌对齿轮啮合振动性能的影响展开研究。

尽管齿面微观几何形貌的形状、大小及分布具有随机性，但基于分形几何的分析表明，齿面微观几何形貌具有统计意义上的自相似性和自仿射性[11]，因此，借助分形几何理论建立齿面微观几何形貌与阻尼特性之间的相互关系，探讨齿面微观几何形貌对齿轮振动特性的影响，以便揭示表面微观几何形貌对齿轮啮合振动特性的影响，为减振齿面主动控制加工方法的选择提供理论与技术参考。

2 基于齿面微观几何形貌的法向接触阻尼近似数学模型

较之于理想光滑齿面，真实齿面的啮合接触面积小于理想光滑齿面的啮合接触面积，如图1（a）所示。为研究方便，将真实齿面间的接触体等效为曲率半径为R 的微凸体之间的接触。受法向外载荷作用，忽略润滑及切向力的影响，各微凸体之间的接触符合Herz 接触假设。等效后的微凸体Herz 接触模型，如图1（b）所示。

图1 粗糙齿面及微凸体接触模型Fig.1 Contact Model of the Rough Surface and Asperity

考虑到齿面接触微凸体产生弹塑性应变时的储能、耗能机理，根据文献[12]，法向接触阻尼Cn与法向接触刚度Kn满足如下函数关系：

式中：η—阻尼耗能因子；

M—基体质量。

依据Herz 积分公式，可推导出作用在任一接触微凸体的法向刚度ki与微凸体接触面积ai的函数关系：

式中：E—弹性模量；μ—材料泊松比；αi—任一微凸体接触面与啮合平面夹角；ai—任一微凸体接触面积。

基于分形几何理论，真实表面上的微凸体的接触面积分布与分形维数存在函数关系[13]：

式中：n（a）—微凸体接触面积分布函数；amax—最大微凸体接触面积；a—任一微凸体接触面积；D—分形维数。

根据图1（a）分析可知，作用在实际接触面上的法向总载荷Fn由同时参与接触的各微凸体共同承担，依据各微凸体在垂直于啮合平面上的变形协调条件，各微凸体在垂直于啮合平面方向上的接触刚度成并联关系，故沿Fn方向的法向接触总刚度为各接触微凸体沿Fn方向上的接触刚度总和。

为便于计算与分析，假设各微凸体的接触法线方向皆垂直于啮合平面，即αi=90°，则基于真实接触面的齿轮法向啮合总刚度Kn可表示为：

式中：ac—临界接触面积。

式（4）中的临界接触面积ac可由下式计算[14]：

式中：λ=H/ey，h=ey/E；H—较软材料的硬度；ey—屈服强度；E—弹性模量。

由此可推得法向接触总刚度Kn为：

结合式（1），并无量钢化后得到基于表面微观几何形貌的法向啮合阻尼的近似数学模型，即：

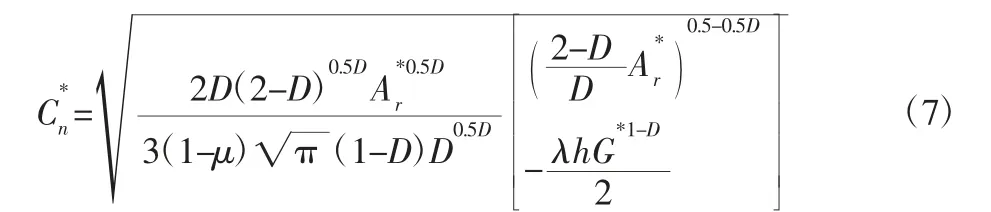
由式（7）可知，法向接触阻尼与分形维数和特征尺度有着密切的关系。

3 实测表面分形参数的计算

表面微观几何形貌因选择的加工方法不同而存在显著差异。以磨削加工和电化学光整加工为例，其加工后的表面微观形貌明显不同，如图2 所示。两表面微观几何轮廓也因此具有明显不同的几何特征，如图3 所示。其中，轮廓测量点间隔为0.125μm，取样长度为4mm。

图2 实测表面三维形貌Fig.2 Three-Dimensional Topography of the Measured Surface

图3 实测表面微观几何轮廓Fig.3 Microscopic Geometric Profile of the Measured Surface

基于对图3 所示表面微观几何轮廓的相关数据及其方差计算，结合FFT 变换后的功率谱获得了表征两种加工方法的表面微观几何轮廓的分形参数，如表1 所示。

表1 表面微观几何轮廓的分形参数Tab.1 Fractal Parameters of Microscopic Geometric Profile of the Measured Surface

由表1 中所示数据可知：与磨削加工相比，电化学光整加工的表面微观几何轮廓的特征尺度和分形维数低。这表明，相对于磨削加工表面，电化学光整加工的表面微观几何轮廓幅值低，且表面微观几何形貌的复杂程度降低，也就是说，表面微凸体的几何形状趋同性得到了提高。

根据图3 所示两轮廓的离散点数据计算获得两表面微观几何轮廓的统计结果，如表2 所示。

表2 表面微观几何轮廓统计计算结果Tab.2 Statistical Results of Microscopic Geometric Profile of the Measured Surface

对表2 中数据的分析表明，相对于磨削加工的表面，在齿轮啮合时，电化学光整加工的表面会有更多的微凸体参与齿面接触，使实际接触面积增加。

利用表1 中所示的分形参数，结合式（7），并设定 η＝3×10-4，另取λ＝0.1，h＝2，μ＝0.3。则可得到由两种加工方法获得的表面的无量纲法向接触阻尼随接触面积的变化规律，如图4 所示。由图4 可知，无论是磨削加工还是电化学光整加工，随着实际接触面积的增加，接触法向阻尼均得到提高；相对于磨削加工的表面，在接触面积相同时，电化学光整加工的表面获得的法向接触阻尼更高。这是因为电化学光整加工使得更多的齿面微凸体参与轮齿啮合，储能、耗能显著，阻尼特征更加明显。这表明：表面微观几何形貌影响齿轮齿面的啮合阻尼特性，不同加工方法获得的齿面，其啮合阻尼特性有差异，并影响齿轮的啮合振动特性。

图4 两种表面的法向接触阻尼随接触面积的变化规律Fig.4 The Variation of the Normal Contact Damping Coefficient of the Two Surfaces with the Contact Area

4 基于阻尼特性的齿轮传动响应的分析

4.1 齿轮传动响应幅值的数值计算

以单扭转自由度的单级直齿圆柱齿轮传动为例。假设其处于理想啮合状态下，不考虑啮合误差及啮合间隙等因素的影响，则其满足动力学方程：

式中：m—齿轮基体质量；c—法向啮合阻尼；k—法向啮合刚度；F—法向啮合力；F0—啮合力均值；ω0—轮齿啮合频率；Fn—n次法向载荷谐波幅值；Ψn—n 次法向载荷谐波相角。

结合式（8），系统的受迫振动响应可表示为：

式中：X0—响应谐波均值；

Xn—n 次响应谐波幅值；

φn—n 次响应谐波相角。

轮齿所受惯性力mω2Xn，阻尼力cωXn及弹性恢复力kXn满足的向量关系，如图5 所示。

图5 任一微凸体受力闭环矢量图Fig.5 Closed Loop Vector Diagram of the Force on the Asperity

结合图5，计算后可得系统的受迫振动响应：

图6 响应幅值随阻尼系数的变化规律Fig.6 The Variation of the Response Amplitude with the Damping Coefficient

4.2 齿轮传动响应幅值的仿真分析

在UG 环境下建立单级圆柱直齿轮副啮合的三维参数化模型，模型基本参数，如表3 所示。将模型及与之配合的Ansys 环境下生成的柔性箱体导入Adams 环境中建立其刚柔耦合虚拟样机模型，如图7 所示。在正对从动齿质心的箱体上表面布置测点，给定主动齿和从动齿的约束及运动条件，采用基于Impact 碰撞函数的接触算法定义齿轮啮合的运算条件，碰撞接触参数，如表4 所示。主动齿轮施加转速1200r/min，从动齿轮施加转矩5000N·mm，仿真时间设定为0.5s，仿真步数为5000，获得测点处最大响应幅值的仿真结果，如图8 所示。

表3 模型参数Tab.3 Parameters of the Model

图7 齿轮减速箱刚柔耦合虚拟样机模型Fig.7 Rigid-Flexible Coupling Virtual Prototype Model for Gear Reducer

表4 Impact 接触算法参数Tab.4 Parameters of the Impact Contact Algorithm

图8 不同法向接触阻尼值下响应幅值的变化Fig.8 The Variation of the Response Amplitude with Different Normal Contact Damping

对图8 的分析表明，增大齿面法向接触阻尼，有助于减小齿轮啮合振动，使振动趋于平稳。仿真结果与根据式（10）所得数值计算结果所呈现出的振动响应幅值随法向接触阻尼的变化规律一致。综上所述，对磨削加工的齿面进行电化学光整加工后处理不失为一种减小齿轮啮合振动的行之有效的方法。齿面经电化学光整加工后可有效提高轮齿法向啮合阻尼，减小齿轮啮合振动。这与文献[6]的相关实验结果一致。

5 结论

（1）齿面微观几何形貌影响齿轮啮合的振动特性，选择合理的加工方法有助于减小齿轮的啮合振动。（2）齿面法向接触阻尼影响齿轮传动振动特性，增大齿面法向接触阻尼有助于减小齿轮啮合振动，改善其振动性能。（3）不同加工方法得到的表面微观几何形貌在微观结构上存在较大差异，表现在其具有明显不同的分形维数和特征尺度。（4）与磨削加工相比，电化学光整加工可降低表面微观几何形貌的分形维数，提高表面微观几何形貌的趋同性。