HS-RNN 在机械主轴振动预报方法中的研究

片锦香，智杰峰

（沈阳建筑大学信息与控制工程学院学院，辽宁 沈阳 110168）

1 引言

随着现代工业的高速发展，机械主轴的平衡显得尤为重要，其动平衡过程也成为国内外学者研究的一项重要课题。主轴在长时间运行过程中，为使机械主轴的运行位置不偏离其几何中心，我们常常采用动平衡策略对振动过程进行优化，降低主轴在高速运转过程中产生的机械振动。

目前，国内外已有诸多关于机械主轴的振动预报及优化计算的研究。文献[1]运用有限元方法对影响转子动平衡系数进行求解，从而确定了不平衡量和振动量之间的关系；文献[2]利用遗传算法对机械转子动平衡方案进行优化计算，使转子在各测试点及不同转速下的振动幅值均降低；文献[3]提出了增加试重的方法使得转子轴承振幅降低，同时利用单平面影响系数法并补加内置平衡块的方案使转子轴承的振动幅值进一步降低；文献[4]通过弹性支撑转子模态动平衡的研究方法，将临界转速下实际转子振动误差缩小，但是该方法的优化效果也不理想，还有提升的空间；文献[5]用模糊控制的方法对主轴转子进行动平衡变步长寻优，此方法在寻优时间上得到提高，但是精度并未得到明显改善；文献[6]在上述方法的基础上对高精度的机械转子动平衡进行检测，进而确定其不平衡量。目前的研究主要集中在增加试重或者用传统的寻优算法优化机械转子的动平衡问题，但是上述方法均存在建模困难和控制精度较低的问题。

因此，提出基于HS-RNN（Harmony Search-Recurrent Neural Network）的机械主轴振动预报模型。HS 算法通过对平衡块位置参数自学习更新，从而提高机械主轴振动预报模型精度。RNN 网络通过不同时刻记忆值的比较并用梯度下降法随机修正误差权重，解决了机械主轴振动预报模型建模困难的问题。最后通过实验对比表明，采用的方法可准确、快速对机械主轴运行过程中的振动幅值进行预报。

2 主轴动平衡过程描述及特性分析

2.1 机械主轴动平衡过程描述

一典型的机械主轴动平衡振动预报过程示意图，如图1 所示。首先，在机械主轴运行过程中，通过安装在主轴外侧的加速度传感器采集主轴当前时刻的转速和振动信号。由于振动由多种因素引起，所以此时的振动信号非常复杂，需要通过信号处理模块提取与当前主轴转速相同频率的振动信号，并将提取出的振动幅值与预先设定的目标振动幅值相比较。根据主轴当前转速的振动幅值与目标振动幅值的偏差，通过主轴振动预报模型对主轴的振动幅值进行预报，并确定不平衡量补偿的平衡块A、B 的当前位置。最后，动平衡装置控制器根据平衡块A、B 位置产生相应的脉冲电压信号，驱动平衡块A、B 转动到目标位置，从而实现机械主轴转子质量的重新分布，消除机械主轴转子的不平衡量，降低机械主轴的振动[7]。

图1 机械主轴动平衡过程工艺流程图Fig.1 Mechanical Spindle Dynamic Balance Process Flow Chart

2.2 机械主轴振动特性分析

机械主轴的平衡控制器的主要作用是计算不平衡量，但是传统的靠经验公式施加负载的方法并不能有效地解决这一问题，而引入的机械电主轴的振动预报模型可准确预报不平衡状态下的主轴振动幅值。机械电主轴转子力学特性，如图2 所示。在主轴运行过程中，其机械主轴高速运转会产生很大的离心力，该离心力与不平衡量、转子距轴心的距离、转速的平方成正比，其离心力公式表示为

图2 机械主轴轴向、径向振动状态图Fig.2 Mechanical Spindle Axial and Radial Vibration State Diagram

式中：m—转子的不平衡量；r—转子半径；ω—主轴转动角速度；n—转速。在内置平衡块质量一定的情况下，平衡块位置补偿主轴产生的不平衡量，从上图机械主轴转子放大的截面振动状态可以看出，转子初始角度为θ0时，假设转子轴向为静止，在径向产生振动，那么此时轴向的曲线方程并不发生变化，径向的振动方程为：

上述对机械主轴的运动特性分析可以看出，通过内置平衡块角度 SA、SB可调节主轴振动幅值，由式（1）～式（2）可以看出主轴振动幅值Ac与转速n、内置平衡头角度SA、内置平衡头角度SB有关，随着Ac的逐渐变化，内置平衡块SA、SB也随之改变，不同转速下转子的振动幅值随平衡块B 所在位置的变化曲线，如图3 所示。在整个机械电主轴预报模型中输入量为平衡块角度SA、SB，输出量为机械主轴的径向振动幅值，由于主轴运行过程中外部干扰因素多，所以其振动幅值与转速之间的变化趋势未呈现线性增长。由图可知，第一、不同转速下，转子的径向振动幅值差异明显，转速越高，其振动不平衡量越大，且各振动幅值之间存在强非线性。第二、在低转速下，转子的径向振动幅值趋于较低的稳定值，在最高转速和最低转速下机械主轴振动幅值存在最优解。第三，转速越高，主轴振动幅值变化趋势越大，预报模型精度表现越低。

图3 不同转速下转子振动幅值随平衡块B 所在的位置的变化曲线Fig.3 Variation of Rotor Vibration Amplitude with Position of Balance Weight B at Different Rotational Speeds

3 HS-RNN 在主轴振动预报模型中应用

3.1 主轴振动预报模型建模策略

机械主轴的振动预报模型主要是为了降低主轴的振动幅值，由于主轴内置平衡块的位置、外加负载和振动幅值之间呈现非线性关系[8]，所以采用RNN 递归神经网络建立主轴的预报模型，其建模策略采用RNN 递归神经网络所建立主轴振动预报模型的输入量有四个，其物理量分别对应机械主轴的平衡块位置SA，平衡块位置SB，负载L，转速n。其随机网络的输出为一个，对应电主轴的物理量为振动幅值的预报值AC。

3.2 HS-RNN 的主轴振动预报模型算法

RNN 递归神经网络最大的优点就是可以有效解决复杂工业环境下的非线性问题，并且兼备具有样本小，计算简单，处理非线性问题拟合的能力。但是由于权值和阈值在初始化过程中具有极大随机性，很容易在重复的训练过程中得到的实际值与预报值有较大偏差，为了保证模型的准确性，应用改进的和声搜索（Harmony Search）算法来提高递归神经网络的寻优精度[9]，与单纯的递归神经网络相比，这种方法精度更高，且预报值的收敛速度更加快。SA、SB为机械主轴内置平衡块的初始设定值，如图4 所示。λA和λB为待定的平衡块的更新位置，et是前一次记忆值和后一次记忆值之间的误差；Ct为t=0 时刻振动幅值的初始记忆值，Lt为t=0 时刻的记忆状态参与下一次的预报值，Ot为t 时刻的输出值，以上三个参数主要是为了对主轴振动幅值进行上一次记忆；U、V、W分别为RNN 中输入到隐藏层、隐藏到隐藏层、隐藏到输出层的梯度下降修正值[10]，主要是为了修正主轴上一次振动记忆值和下一次振动记忆值的误差。

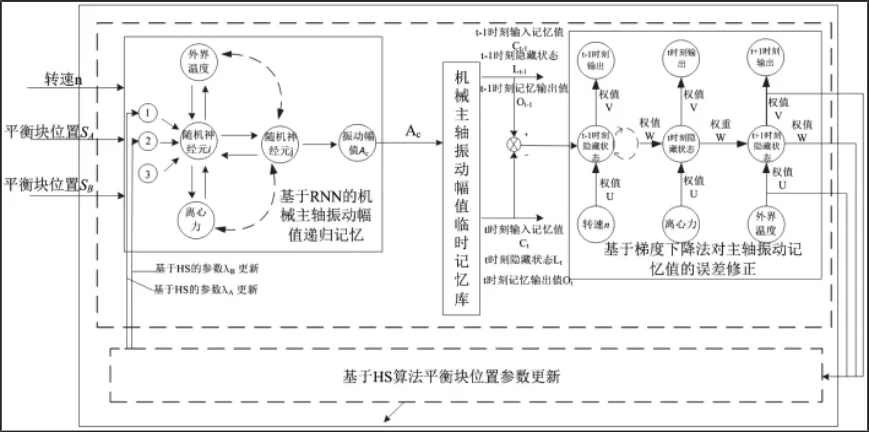
图4 基于HS-RNN 机械主轴振动预报模型的算法策略图Fig.4 Algorithm Strategy Diagram Based on HS-RNN Mechanical Spindle Vibration Prediction Model

3.2.1 基于RNN 的机械主轴振动值递归记忆

递归神经网络中的记忆功能即记忆函数，其值越大记忆性越好，设ft为递归网络记忆过程的记忆更新函数，其机械主轴内置平衡块位置与记忆函数的关系，如式（3）所示。

式中：xt—平衡块的角度向量；Ot—t 时刻的输出量。通过g 在Ot输出函数中的给定值获得对主轴上一次位置的记忆值。

3.2.2 梯度下降法对主轴振动记忆值的误差修正

机械电主轴针对A、B 两个平衡块上一次记忆位置和下一次位置之间的差异存在实时误差，即输出振动误差，在误差修正阶段，每一个误差梯度下降法修正得出一个平衡块目标位置值[11]，如式（4）所示。

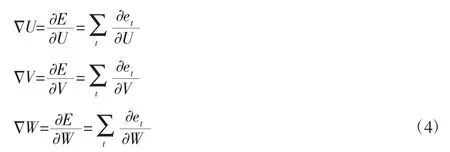
在内置平衡块的位置角度的搜索修正过程中，应该运用的链式迭代法则来实现不同时刻参数的实时共享，这样不仅可以实时修正误差，而且能减少训练参数，快速提取机械主轴运行过程中因不平衡量引起的主轴振动偏差，如式（5）所示。

3.2.3 HS 算法平衡块位置参数更新

全部平衡块位置角度记忆、比较、修正结束后若再没有新的不平衡量进行更新，则认为此运行状态陷入局部最优，该时刻下的内置平衡块位置应该舍弃，此时由式（6）对内置平衡块的位置进行更新，产生一对新的平衡位置。

3.3 HS-RNN 主轴振动预报模型算法实现步骤

运用改进的HS-RNN 来提高预报精度，流程图，如图5 所示。

图5 改进的和声搜索算法流程图Fig.5 Improved Harmonic Search Algorithm Flow Chart

基于机械电主轴振动预报模型步骤如下：

（1）初始化递归神经网络与和声搜索算法中的所有参数，和声库大小HS、最大迭代次数D。确定机械电主轴内置平衡块位置的变化范围，并在该范围内根据经验选定一个初始平衡位置SA和SB。

（2）将该值测得的下一时刻不平衡量代入RNN 网络中进行隐藏层之间的权值搜索，得出机械主轴的振动初始记忆值，根据记忆权重W 和下一时刻权值Wn-1进行记忆总结，判断此刻的记忆结果是否满足终止条件。

（3）当记忆结果满足终止条件Lt＜0.5 时，说明此时的记忆误差在可接受范围内，则初始记忆值为预报主轴振动最小值，如果Lt>0.5，则进行（4）。

（4）用梯度下降法修正递归神经网络中的参数ΔU、ΔV 和Δ W 按照预设定的值进行比较，如果没有达到修正值则返回记忆比较；如果按照式（4）中修正值达到主轴振动位置目标位置，则进行步骤5 对内置平衡块进行位置更新。

（5）按照式（6）采用新旧位置的最优和最差原则对通过和声搜索自适应因子SA 更新后的解位置更新（在此时如果自适应因子中的随机数Rand5≥SA 则返回初始记忆值继续执行（2），如果Rand5＞SA 则对机械电主轴内置平衡块的位置进行更新，更新到目前为止的最优解。

4 实验研究

4.1 实验平台描述

机械主轴动平衡实验平台实物图，如图6 所示。机械电主轴的型号为CJ190Z4，电动机转动通过传动电动机的皮带联动机械电主轴使其转动，通过机械电主轴动平衡实验装置测取所需的样本数据，样本数据的输入量为机械电主轴的A、B 平衡块的位置SA和SB，电主轴的左侧是转速传感器，可通过电主轴性能测试系统调节其转速，电主轴的右侧是其位置传感器，可实时测得电主轴的振动偏差大小。

图6 实验平台实物图Fig.6 Experimental Platform Physical Map

4.2 实验参数设置

实验过程中选取转速范围为600-2800RPM，负载为10N、20N、30N 条件下测得的实验数据建立样本数据库，平衡块A、B的角度变化范围从0°到360°，两者之间的角度相差15°。振动幅值采用主轴径向位置的振动幅值，样本数据库采集6624 组数据建立机械主轴振动预测模型，具体参数，如表1 所示。

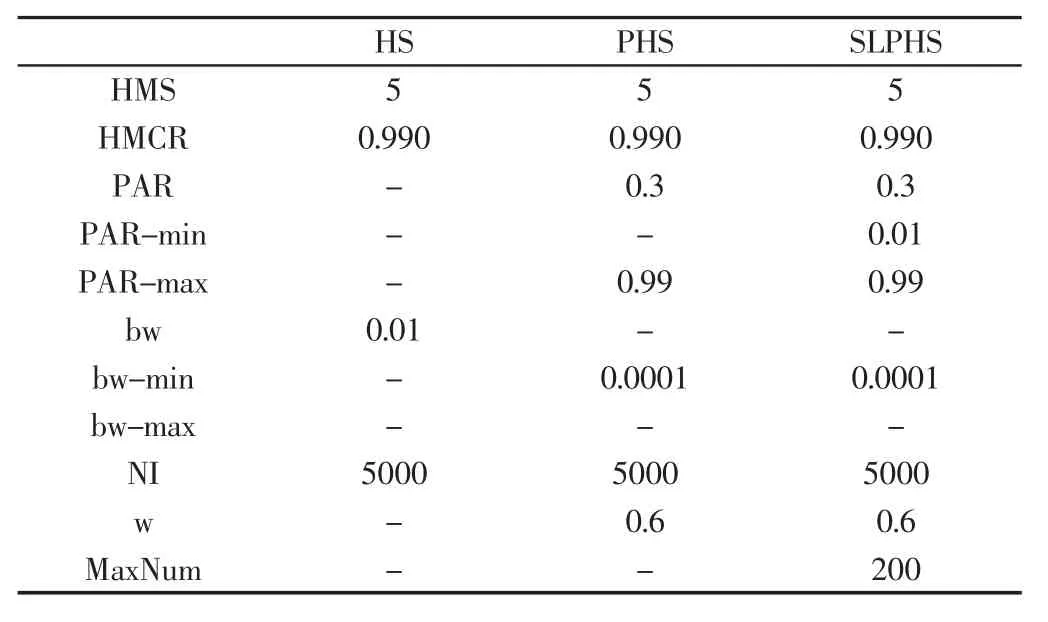
表1 实验参数设置Tab.1 Experimental Parameter Settings

4.3 实验结果分析

用改进的HS-RNN 处理的平衡块位置优化参数对比在机械主轴振动幅值预报平均时间方HS-RNN 的改进效果均优于其他两种优化算法，其在模型预报精度方面提升更明显。

将样本数据库的数据带入HS-RNN 算法，运算仿真结果可以得出，实际振动幅值略大于预测值，在电主轴转速为2000RPM时，其振动幅值最大，其误差在（4～6）%之间，最大的误差为5.12%，所以在转速较低时其加工精度相对较平稳，但是随着转速逐渐变大其不平衡量也越大。

我们对样本数据库从第1 组至第5000 组数据进行RNN 训练，每组数据包含4 个输入神经元和一个输出神经元。基于RNN递归神经网络、基于HS-BP 神经网络和基于改进HS-RNN 预报模型的均方误差随训练次数的变化曲线，如图7 所示。由图可知，使用改进后的HS 算法优化后的权值和阈值进行RNN 训练的误差值要比直接使用RNN 随机网络生成的权值和阈值明显变小，说明改进HS-RNN 的可行性。

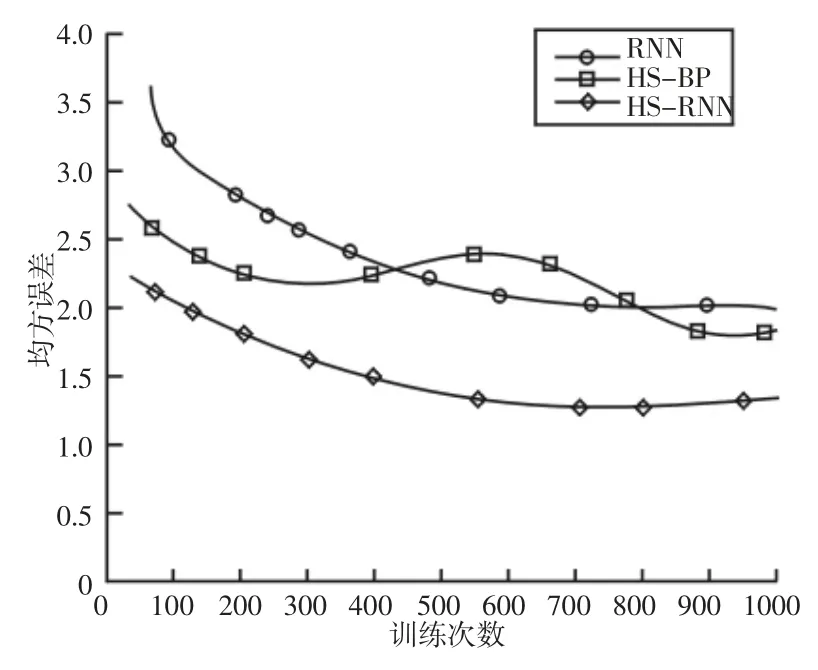
图7 不同预报模型下训练时均方误差对比图Fig.7 Comparison of Mean Square Error of Training Under Different Forecast Models

图8 基于RNN、基于HS-BP 预报模型结果误差对比图Fig.8 Based on the RNN，HS-BP Model Based on the Results of the Error Comparison Chart

在三种预测模型中，基于HS-RNN 的预测结果由于和声搜索算法可实时更新振动幅值位置，所以相比其它两种预测模型要精确，如图8、图9 所示。

为了证明方法的有效性，将上述随机网络预测模型和改进前的和声搜索算法进行比较，其误差下降曲线，如图10 所示。随着迭代次数的增加，机械电主轴的振动误差并没有趋于稳定，收敛速度也没有明显改善，而建立的预测模型在精度和收敛速度上都优于改进前的方法。

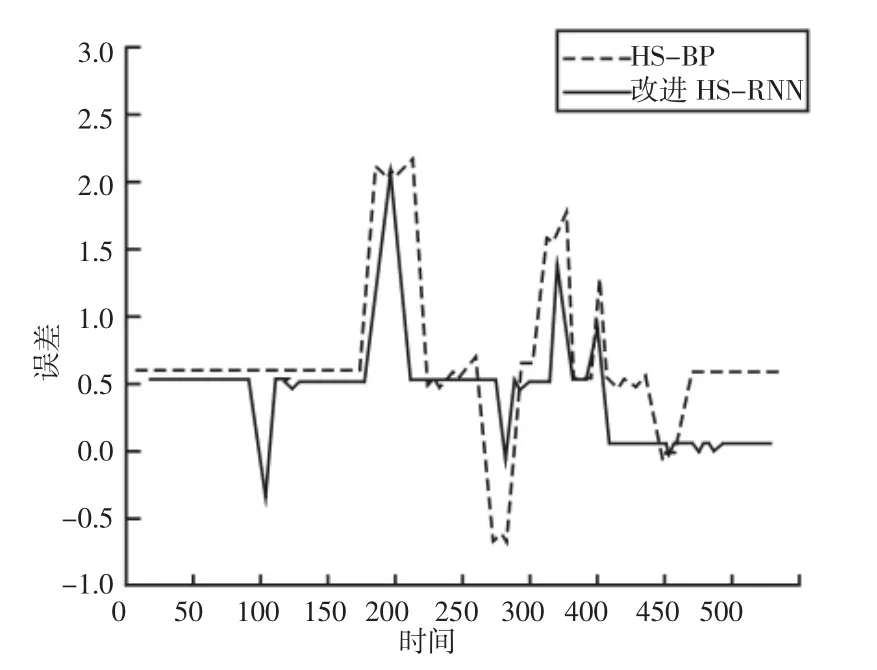
图9 基于HS-BP、基于HS-RNN 预测模型结果误差对比图Fig.9 Based on HS-BP，Based on HS-RNN Prediction Model Error Comparison Chart

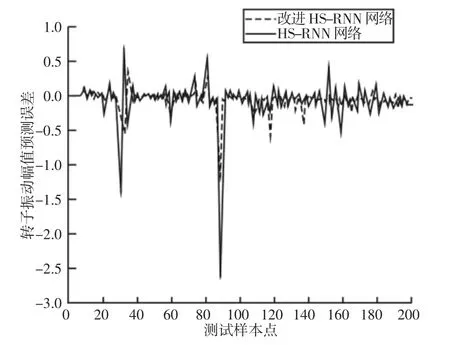
图10 两种预报模型误差对比曲线Fig.10 Two Kinds of Forecast Model Error Comparison Curve

5 结论

针对机械主轴振动预报过程建模困难和模型精度低的问题，采用基于改进HS-RNN 算法对机械主轴振动预报模型进行方法研究。用RNN 递归神经网络达到对机械主轴振动预报过程建模的目的，采用HS 算法通过对平衡块位置参数自学习来提高预报模型的精度。结果表明，提出的方法较传统方法能够快速地建立主轴振动预报模型，提出的算法具有控制精度高的特点。与相似性方法相比，本方法能够对机械主轴振动幅值进行预报，且及时调节动平衡过程，从而可以将机械主轴振动预报模型的振动误差控制在目标振动范围内，达到提高机械主轴控制精度的目的。