阶梯式溢洪道泄洪能力随几何形状变化的数值模拟计算

吴春水

（昌吉回族自治州呼图壁河流管理处，新疆 昌吉 831100）

1 引言

溢洪道是在蓄洪坝和拦洪坝上设置的一种水工建筑物，用于释放不能安全储存在水库中的多余水，当洪水超过水库蓄水能力时，水流越过溢洪道顶部，并沿着泄槽加速，在坡脚处产生高速冲刷，会对水工建筑物下方的天然河道带来不利影响，作为一种补救措施各种形式的消能机制已在实践中得到广泛应用，如简单的护坦、消力池、冲击池、折流槽和消力塘等。尽管这些方法已被证明在耗散能量方面是有效的，但其建设成本大，并且会影响溢洪道结构完整性的缺陷，可能导致大坝故障[1]。

因此提出一种阶梯形溢洪道，代替传统的光滑溢洪道。在坝顶附近到坡脚的仰拱处设置一系列阶梯式溢洪道，阶梯作为粗糙度元件，使下泄水流产生巨大能量损失，降低水流末端速度。近年来，阶梯式溢洪道以其低成本、高性能等优势，快速在蓄洪坝和拦洪坝中广泛应用。但阶梯式溢洪道的水流计算建模方面进展甚微，基于此，本文使用有限元方法对阶梯式溢洪道的水流进行建模，对阶梯式溢洪道水力特性进行模拟研究，为大坝安全运行提供可靠依据[2～4]。以昌吉呼图壁河流域某拦洪坝溢洪道模型为研究对象，对其进行同比例建模研究。

2 模型特征参数设置

溢洪道倾角为60°，在其下端有一段圆弧用来连接溢洪道和消力池，使下泄水流平稳过度。模型溢洪道从坡脚到坝顶的总高度Hs等于380 mm，由上到下沿泄槽引入台阶，台阶选择高度为1/20Hs（19 mm）的大台阶或高度为1/40Hs（9.5 mm）的小台阶，模型溢洪道整体高度为342 mm，通过改变溢洪道上下部台阶高度共建立四个模型，具体参数见表1。

表1 溢洪道模型具体参数设置

初始条件设置见图1，在底部边缘和溢洪道沿线（所有标记为A的线）施加固定墙边界条件，初始水面由标记为B的三条直线模拟。在入口（标记为C的直线）处，给定了0.107 m/s的均匀流速，该值是通过将流速除以上游水深的实验测量值计算得出的。

图1 溢洪道模型初始条件设置

模型网格划分见图2。由多个三角形三节点单元网格组成，在位置1、2和3处使用高分辨率网格，以便解析（或捕获）更复杂的水流运动，其他位置均采用相似的网格。表1给出了每种情况下使用的网格总数[5]。

图2 分析中使用的有限元网格划分

3 数值分析及结果讨论

采用ADINA软件中计算流体力学模块ADINA-F模拟阶梯式溢洪道的水流，ADINA-F是一种通用的有限元程序，可用于模拟各种流体流动问题，实验设置部分概述的所有四个案例均已建模，为方便比较，同时对光滑溢洪道进行模拟，模拟过程的一个关键点是对坝顶之前的上游、溢洪道上方和坡脚之后的下游的整个水面精确跟踪，水流在溢洪道上的流动本质上是湍流，因此采用k-ε紊流模型，除上述参数设置外，其余所有默认参数由ADINA-F提供[6]。

3.1 瞬态过程模拟

瞬态过程均包括200个时间步，每个时间步的恒定幅度为0.005 s，总计模拟时间为1.0 s，瞬态模拟过程见图3。

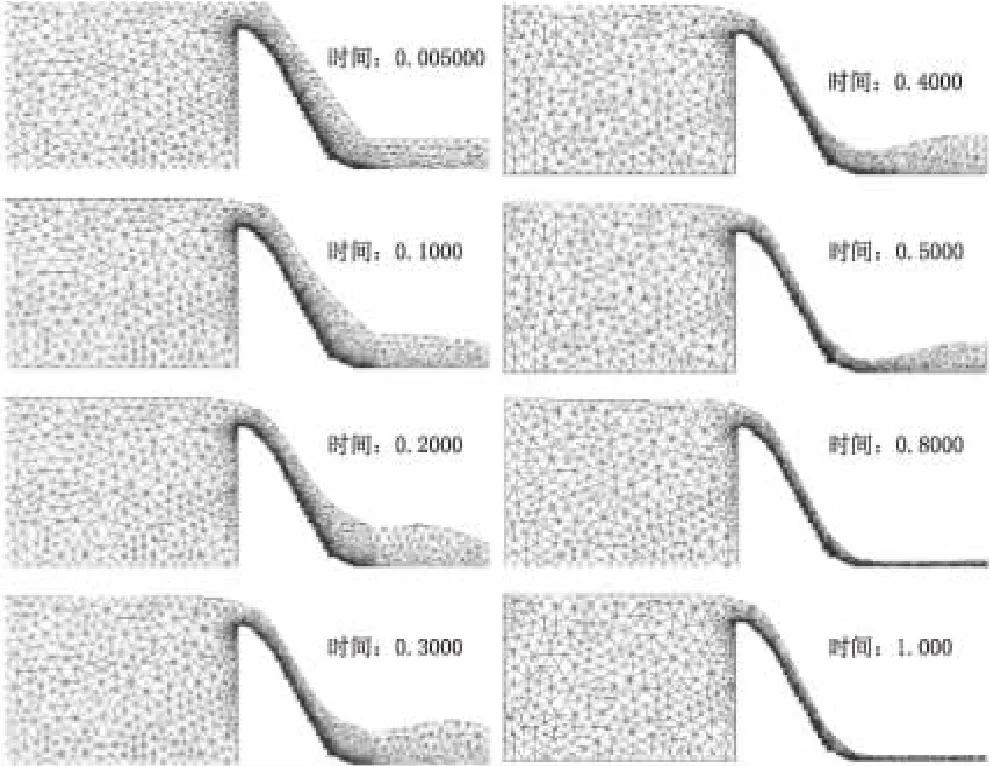
图3 溢洪道水流瞬态模拟过程

图3为溢洪道水流瞬态模拟过程，描述了网格的几何结构随时间的变化，一共分为200个时间步，波峰处和波峰下游的自由面部分在0.005 s～0.8 s（共160步）的时间跨度内，在这个时间范围内水流形态急剧演变。在0.8 s～1.0 s之间的时间跨度（共40步），网格几何没有明显变化，其他情况下网格几何演化的稳态解都相似。

3.2 速度矢量分布

图4为模型4在溢洪道三个不同位置的速度矢量图，从图中可以明显看出，滑行水流在台阶边缘滑行，循环区（或漩涡）在台阶面形成的三角形凹坑中形成。随着滑行水流速度的增加，涡旋水流速度不断增大，且小于滑行水流流速，约比滑行流的速度减少1/4。其中图4（a）代表溢洪道上部水流速度矢量分布情况，从图中可以看出滑行水流以及涡旋水流流速范围在0.175 m/s～1.575 m/s之间；图 4（b）代表溢洪道中部水流速度矢量分布，从图中可以看出滑行水流以及涡旋水流流速范围在0.525 m/s～1.925 m/s之间；图 4（c）代表溢洪道下部水流速度矢量分布，从图中可以看出滑行水流以及涡旋水流流速范围在0.525 m/s～2.275 m/s，其他三个模型的速度矢量图都相似。

图4 模型4溢洪道三个不同位置的速度矢量图

3.3 阶梯溢洪道表面压力分布

当工作水头突然增大，如洪水爆发等，溢洪道的一些位置可能产生负压，出现空化和振动，因此有必要研究该状态下阶梯溢洪道的压力分布情况。选取溢洪道两个典型位置，靠近溢洪道的上部中间、底部中间，4个模型同一时间步，x轴方向（水平方向）和y轴方向（垂直方向）的压力分布，见图5。台阶表面的x和y坐标上的压力变化在两个位置都遵循类似的模式，沿x轴水平表面，压力先减小，后增大，在台阶尖端之前达到最大值，到达尖端处时，压力急剧下降，见图5(a)。这种最大压力是由落水对台阶的影响引起的；沿y轴垂直表面，随着从拐角处向下距离的增加，压力持续下降，并在靠近拐角处发生急剧变化，见图5（b）。在水平面x轴方向会产生波动变化为正压，在垂直面y轴方向产生的压力在正负之间进行波动。光滑溢洪道泄槽的压力，在第一个位置处产生负压力接近零，在第二个位置处产生较小的正压力。

图5 阶梯溢洪道表面压力分布图

3.4 阶梯消能率计算

在消力池的设计中，须了解溢洪道底部的剩余动能，溢洪道的能量损失采用式（1）～式（6）进行计算:

式中:E0、E1、E2分别为上游总水头、下游平滑溢洪道及阶梯溢洪道总水头，m；H0、H1、H2分别为上游断面水面高程、平滑溢洪道及阶梯溢洪道水面高程，m；V0、V1、V2分别为上游断面平均流速、下游平滑溢洪道及阶梯溢洪道断面平均流速，m/s；a为流速系数，取1；η、η1、η2分别为阶梯增加消能率、平滑溢洪道消能率及阶梯溢洪道消能率，%。

表2 阶梯消能率计算结果

通过计算可知模型 1～4的能量损失分别为:51.6%、53.1%、52.2%和48.7%，而光滑溢洪道模型的能量损失为30.5%。因此模型1～4溢洪道增加的能量损失值分别为:21.1%、22.6%、21.7%和 18.2%；这些数值与 Chatila和 Jurdi[7]报告的能量耗散率相当，同样说明了模型计算的准确性。

4 结论

通过有限元计算流体力学模块ADINA-F采用k-ε紊流模型与流体体积分数(VOF)法相结合详细揭示流场的时均流特性和紊动特性，对模型1～4溢洪道水流进行模拟，结果显示与一般流动特性定性一致，并且与测量的自由表面轮廓一致，整个求解过程只需20 min即可完成，说明了仿真软件作为一种可用于灵敏度分析的工具的合理性，并且可以考虑多种情况，采用相同的求解过程来模拟在不同水头下运行的各种阶梯溢洪道结构，以优化阶梯式溢洪道的性能，是研究阶梯溢洪道等泄水建筑物水流运动规律及消能机理的有效途径。