基 于 BiLSTM 和 Bootstrap 方 法 的风电功率区间预测
2020-08-17俞志程吴海东
薛 阳, 张 宁, 俞志程, 吴海东, 李 蕊
(上海电力大学 自动化工程学院, 上海 200090)
0 引言
在全球化石能源日渐枯竭的背景下, 可再生能源的开发和利用已成为世界各国关注的焦点。风能作为可再生能源的重要组成部分, 在改善生态环境、 促进能源消费结构转型中发挥了关键作用。由于风能具有较强的间歇性和随机性,导致风电机组的功率波动。因此,准确可靠的风电功率预测对于降低运行成本、 提高电力系统的安全可靠性具有十分重要的意义[1],[2]。
目前, 国内外学者针对风电功率的预测方法开展了大量研究,主要包括物理方法、基于统计学的方法和组合预测方法。其中,物理方法对风机及天气等相关信息需求较多,预测工作较复杂,而统计学方法仅需通过历史数据建立影响因素与风电功率的关系即可完成预测。研究表明,单一的预测方法大都存在精度较低的缺陷,因此,基于统计学的组合预测方法受到了广泛关注。 文献[3]提出了一种应用改进的乌鸦算法对回声状态神经网络输出层连接权重矩阵进行优化的短期风电功率组合预测方法。 文献[4]提出了一种结合卷积神经网络和门控循环单元的超短期风电预测方法。 上述文献主要针对风电功率进行确定性预测,精度不高。在风电机组实际运行中, 确定性预测方法难以满足系统运行对准确度的需求, 故有学者在组合方法的基础上提出了区间预测方法, 以弥补确定性预测方法的不足。
区间预测方法充分考虑了不确定性因素引起的预测误差, 在给定置信水平下得到风电功率的上限和下限,为调度提供更有效的信息。相关学者已经在区间预测领域取得了一定的成果。 文献[5]提出了基于人工蜂群改进的ABC-BP 神经网络算法,该方法具有准确性高、均方误差小的优点,同时收敛速度加快,具有更好的稳定性和鲁棒性,可以有效预测发电量的变化。 文献[6]提出了一种基于深度学习分位数的预测方法, 运用Adam 随机梯度下降法在不同分位数条件下对长短期记忆网络(LSTM)的不同参数进行估计,得出未来时刻风电功率的预测区间。 上述方法主要从引入优化算法的角度对风电功率进行建模预测, 为风电功率区间预测提供了新的思考, 但并未从结构上对神经网络进行改进, 存在进一步提高预测精度的可能。
为了有效解决上述问题, 本文提出了一种基于双向长短期记忆网络 (BiLSTM) 和自助法(Bootstrap)的组合预测模型B-BiLSTM。 首先,构建包含原始风电功率数据和相应的历史风速数据的多变量时间序列样本。其次,将样本进行归一化处理, 并按照一定比例将样本划分为训练集和测试集,再利用Bootstrap 方法进行重新采样获得多个训练样本。 接下来, 构建风电功率区间预测的BiLSTM 模型,并利用人工蜂群算法对网络超参数进行优化,以提高模型的预测精度。 最后,获得风电功率区间的预测结果。 算例分析结果表明,与LSTM 等其他方法相比, 本文提出的预测方法在功率波动明显的情况下具有更窄的带宽, 能更好地预测未来风电功率的变化趋势。
1 Bootstrap 方法
1.1 风电功率的影响因素
风电功率具有很强的波动性和随机性, 影响因素主要表现在风速、风电转换过程、风电机组固有特性以及风电系统外部4 个方面。 上述因素共同作用,造成了风电功率数据的严重非线性,增加了风电功率预测的难度。 表1 为各影响因素的具体内容。

表1 风电功率影响因素Table 1 Affecting factors of wind power
1.2 Bootstrap 原理
Bootstrap 方法由Efron 提出, 已被广泛应用于时间序列的重采样问题和区间预测问题[7]~[9]。尤其在数据波动明显的条件下, 该方法可以显著提高区间预测的准确率。
本文采用非参数化的Bootstrap 进行重采样过程,基本原理:设实际测量的数据集容量为M,对数据集中参数进行估计; 当选中原始数据集中的一个数据, 它被再次选中并被再次添加到训练集中的概率为1/M, 有放回的抽取M 次, 得到Bootstrap 样本集,按照上述步骤重复N 次,就可以得到N 个Bootstrap 样本集,在每一个样本集上都有对应的估计量, 利用这个样本集来反映估计值的概率分布和随机性特征。
在样本的获取过程中引入Bootstrap 方法能够较好地克服风电功率时间序列的异方差性。 本文采取通过多次采样获得多个训练样本的方法提高模型参数估计的精度,从而提高预测的精度。
1.3 风电功率预测区间的构造
风电功率区间预测利用历史风电功率和风速数据集H 建立Bootstrap 样本,采用基于点预测方法得到每个Bootstrap 样本的风电功率预测值,通过该预测值序列构造一个预测区间。
(1)获取历史风电功率和风力因素数据集,建立原始样本序列Q=[q1,q2,…,qr],q∈N+。
(2)按照1.2 节中方法建立N 个Bootstrap 样本P1,P2…,PN。
(3)对每个Bootstrap 样本进行点预测建模,获得预测值。
(4)通过步骤(3)中N 个点预测模型分别对测试样本进行预测,获得包含N 个预测值的序列S。
(5)利用百分位数区间估计法对S 进行估计,得到风电功率的预测区间。
2 双向长短期记忆神经网络及其优化
2.1 循环神经网络
循环神经网络 (Recurrent Neural Network,RNN)是一种具有记忆能力的递归神经网络,可以用来分析时间序列数据。图1 为RNN 的拓扑结构图。 图中:X 为输入序列,X=(x0,x1,…,xt);Y 为输出序列,Y=(y0,y1, …,yt);W 为隐含层状态,W=(w0,w1, …,wt);A 为从输入层连接到隐含层的权重矩阵;B 为从隐含层到输出层的权重矩阵;C 为隐含层自反馈权重矩阵。

图1 RNN 的拓扑结构图Fig.1 Topology diagram of RNN
RNN 可以看作一个在时间上传递的神经网络, 但在对长序列进行训练时会出现梯度消失或梯度爆炸现象。为了解决这个问题,有学者提出了LSTM 神经网络。
2.2 BiLSTM 神经网络
LSTM 是RNN 的一种特殊变体,其隐含层由普通神经元被替换为包含门控机制的记忆单元,从而解决了梯度消失问题, 但LSTM 无法编码从后到前的信息,BiLSTM 的提出弥补了其不足,BiLSTM 由前向和后向LSTM 结合而成。图2 所示为BiLSTM 的拓扑结构, 用于学习特定时间的过去特征和未来特征[10]。与传统神经网络算法相比,BiLSTM 具有记忆能力,并且前向传播层和后向传播层共同连接到输出层,考虑了数据间的关联性,使输出结果更加精确。
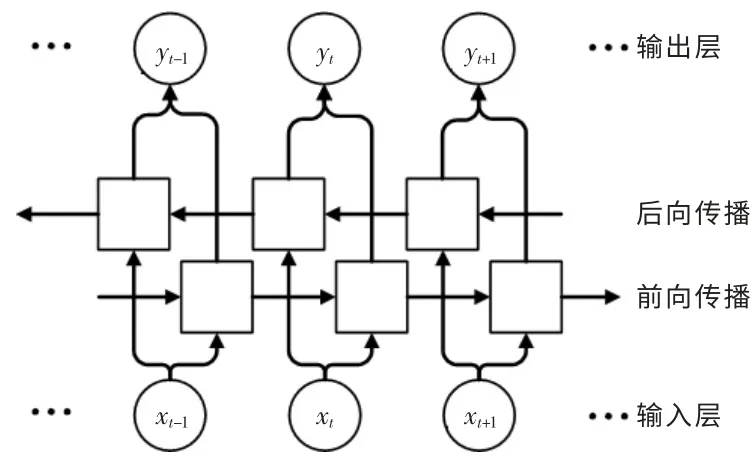
图2 BiLSTM 的拓扑结构图Fig.2 Topology diagram of BiLSTM
2.3 基于人工蜂群算法的BiLSTM 模型超参数优化
人工蜂群算法是由Karaboga D 受蜂群配合寻找食物的行为启发而提出的一种优化算法[11]。因具有操作简单、控制参数少、鲁棒性强的优点,在多目标优化中具有较快的收敛速度和更高的精度。 利用人工蜂群算法改进BiLSTM 神经网络(ABC-BiLSTM),将求解BiLSTM(初始权重和偏置项)的最优解变换为求解蜂群最优食物源。通过优化后的ABC-BiLSTM 模型对数据进行训练,能够在更短的时间内获得更加精确的结果。 优化步骤如下。
(1)构建BiLSTM 网络。 将BiLSTM 网络的输入层和隐藏层、 隐藏层和输出层之间的参数用行向量表示。
(2)初始化ABC 的训练参数。 将食物源的个数N、蜂群大小、采蜜蜂数量、跟随蜂数量、解的数量、 失败次数极限值以及最大循环次数作为训练参数。
(3)每个食物源的适应度函数值fitm为

式中:fitm为第m 个解的适应度值,m=1,2,…,N;fm为目标函数, 本文采用BiLSTM 神经网络的预测值与实际值的交叉熵作为目标函数。
(4)采蜜蜂在当前食物源Xm领域搜索产生新食物源Vm,并依据贪婪原则选择适应度值大的食物源。
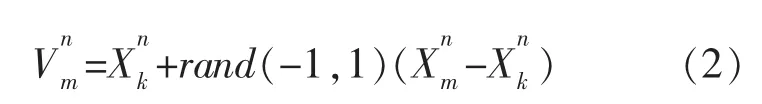
式中:k∈{1,2,…,n}是随机产生的,且k≠m;n∈{1,2,…,D},D 为行向量维数。
(5)跟随蜂按概率P 在当前食物源进行搜索寻找新的食物源, 并根据贪婪原则选择适应度值大的食物源。

式中:Pm为第m 个解的概率。
(6)如果食物源没有更新,则其对应的更新失败次数加1。 如果食物源的更新失败次数超过了极限值,则跟随蜂变为侦查蜂,根据式(2)寻找新的食物源,并将失败次数初始化为0。 假设舍弃的食物源是Xm和n,则有:
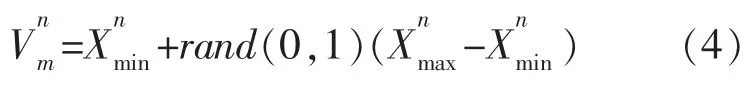
(8)将ABC 得到的最优解作为BiLSTM 的初始权重和偏置项,训练BiLSTM 神经网络。
(9)将得到的结果用于仿真预测。
ABC-BiLSTM 的流程图如图3 所示。
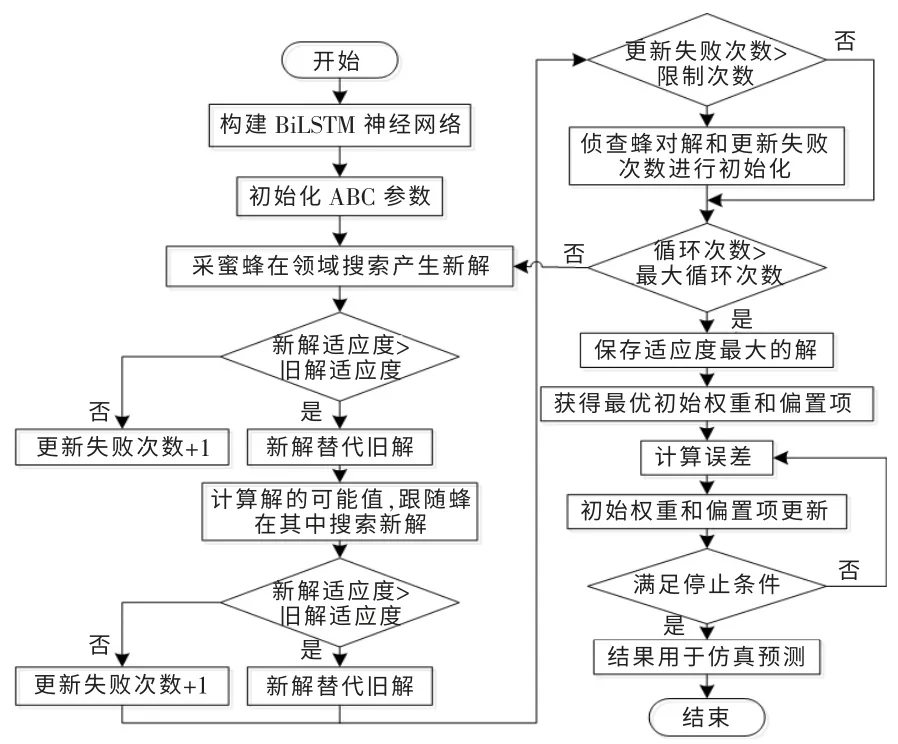
图3 ABC-BiLSTM 流程图Fig.Flow chart of ABC-BiLSTM
3 基于B-BiLSTM 方法的风电功率区间预测模型
风电功率数据本身具有波动特征,且受风速、风电转换过程、风电机组及其他外部因素的影响,因此,其功率序列存在很大程度的非线性特性,使用常规学习预测方法对预测精度的提升较为有限。 考虑到Bootstrap 方法在克服风电功率时间序列的异方差性的突出优势, 以及BiLSTM 在时序数据建模中的优异表现, 本文提出一种B-BiLSTM 组合预测模型,在保证预测精度的同时缩小预测区间面积。 具体建模过程如下。
(1)获取原始风电功率数据和相应的历史气象数据,构成多变量时间序列样本,对样本进行归一化处理至[0,1]区间,并按照9∶1 的比例划分训练样本与测试样本。
(2)针对风电功率序列的波动性特征,采用Bootstrap 方法对样本进行重采样处理, 得到多个训练样本和测试样本。
(3)构建BiLSTM 神经网络预测模型,并采用ABC 算法对预测模型的超参数进行寻优,获得最佳的超参数组合。
(4)训练优化后的预测模型,并输入测试样本,获得给定置信水平下的区间预测结果。
(5)与实际数据对比,通过多种指标来评估预测模型的预测性能。
4 算例分析
4.1 模型评价指标
模型的评价指标主要有预测区间覆盖率(PICP)和平均预测区间宽度(PINAW)两方面。
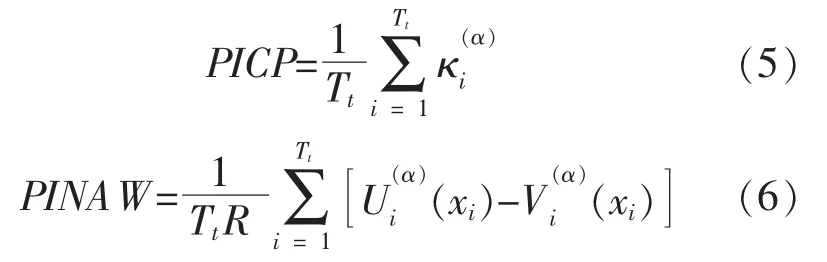
式中:Tt为预测样本数;κ 为布尔量, 如果预测值包含于预测区间内,则κ=1,否则κ=0;R 为预测值的变化范围,用于对PINAW 进行归一化处理。
4.2 预测结果分析
算例所用数据为我国某沿海城市风电场2018 年的风电功率实测数据, 采样周期为15 min。在131 400 条原始数据中,按照9∶1 划分为训练样本和测试样本。 设置Bootstrap 抽样次数为1 000 次,为保证预测结果的可靠性,通常选取较高的置信水平, 本文选用的置信水平为90%和95%。ABC 中的蜂群大小为200,食物源的数量为100,极限值为100,最大循环次数为25。将本文提出的预测方法与相同置信水平下基于Bootstrap的LSTM(B-LSTM)等方法的预测结果进行对比,图4 和图5 分别为在90%的置信水平下,不同日期下24 h 内B-BiLSTM 和B-LSTM 的风电功率区间预测结果。
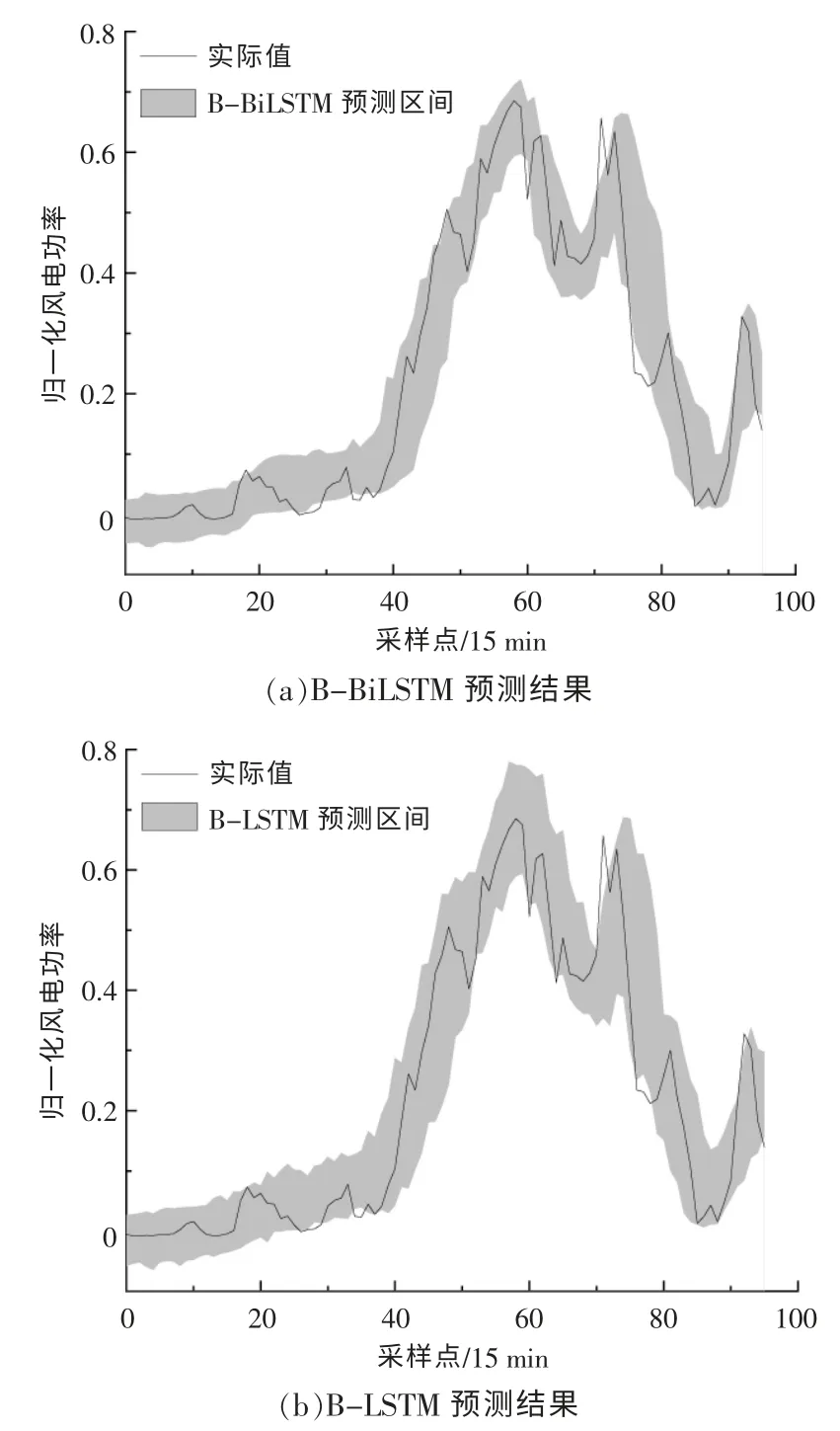
图4 4 月23 日预测结果对比Fig.4 Comparison of prediction results on April 23
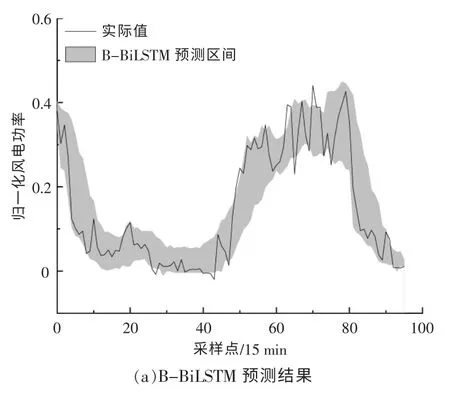
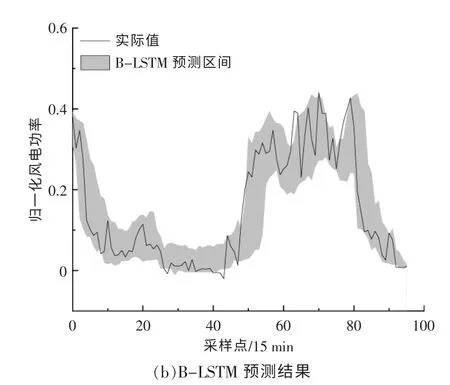
图5 10 月23 日预测结果对比Fig.5 Comparison of prediction results on October 23
由图4,5 可知: 在同一日期下, 相较于BLSTM 的预测结果,B-BiLSTM 的预测区间可以更大程度地覆盖实际的输出功率点, 且比B-LSTM具有更窄的带宽;不同日期下,随着风电功率的波动性增强,B-LSTM 模型稳定性降低且带宽明显增加, 而B-BiLSTM 模型在保证覆盖率和稳定性的同时,带宽基本不受影响,验证了其对于提升预测性能的有效性。
4.3 算法性能对比分析
表2 为B-BiLSTM 与B-LSTM 方法和传统方法在不同置信水平下预测结果的评价指标对比。
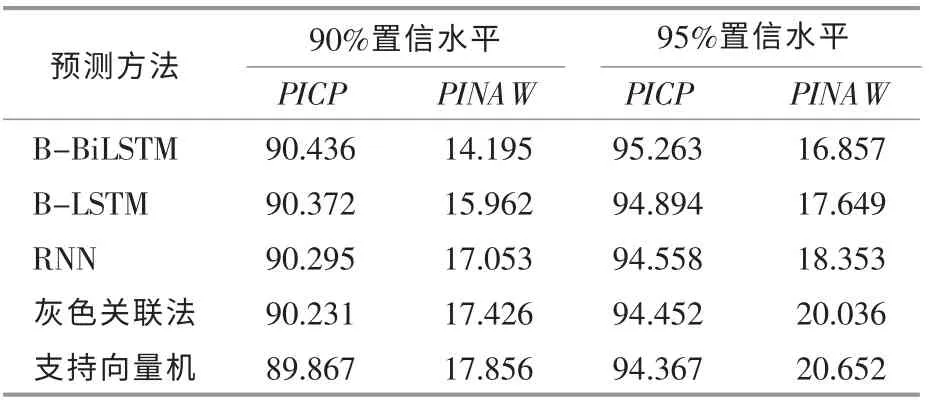
表2 不同置信水平下各算法对比结果(4 月23-29 日)Table 2 Comparison results of different algorithms at different confidence levels(April 23-29) %
由表2 可知: 随着置信水平的提高, 带宽增大,但覆盖实际功率点的效果更佳;在不同的置信水平下,相较于其他方法,本文提出的B-BiLSTM方法具有更高的PICP 和更窄的PINAW。
5 结论
本文针对风电功率的不确定性提出了一种基于B-BiLSTM 的风电功率区间预测方法, 得到以下结论。
①在分析风电功率特征及影响因素的基础上,采用Bootstrap 方法对样本进行重采样,提高了模型参数估计的精度。
②利用BiLSTM 神经网络的循环网络结构和门控特性,实现对序列的时序关联性捕捉,再引入ABC 算法对BiLSTM 神经网络的超参数进行优化,克服经验选取的弊端,使预测结果更加精确、更具鲁棒性。
③以PICP,PINAW 为评价指标,利用相同置信水平下风电场实际数据与基于Bootstrap 的LSTM 神经网络及传统方法进行对比, 算例结果表明,在保证一定PICP 的情况下,本文提出的区间预测方法具有比其他方法更高的PICP 和更窄的PINAW。
