空滑迫降模拟试飞方法研究

段义乾，秦俊生，徐王强

（1.航空工业洪都，江西 南昌，330024；2.空装驻南昌地区军事代表室，江西 南昌，330024）

0 引 言

空滑迫降是发动机停车或发生故障时保证飞机安全的应急措施，这不仅是对飞行员驾驶技术的考验，更是对其心理的考验，一旦迫降失败，很可能发生重大事故[1]。飞行迫降的成功与否，在心理上取决于飞行员是否具有处置空中特情的思想准备，在技术上取决于飞行员是否具有处置空中特情的经验和能力，而这些又与飞行员是否掌握了相应的迫降理论知识和模拟训练的经验密切相关[2]。

考虑到发动机停车风险，在模拟训练中常采用发动机慢车来模拟停车情况，结合打开减速板增加阻力的形式，进行模拟空滑迫降试飞[3]。模拟空滑迫降能够 “逼真模拟” 发动机停车的真实情况的前提在于达到相近的 “空滑比” ，即飞机能用相似的轨迹倾角下滑进场着陆。当发动机慢车推力与减速板增加阻力不匹配时，模拟的空滑比与理论空滑比将存在一定的差值，进而导致采用该方法模拟的空滑迫降过程不够真实。因此，在实际工程应用中采用上述方法来模拟空滑迫降时，需提前进行理论分析，计算发动机油门的大小以保证模拟空滑比与理论无动力空滑比保持一致。本文以某型飞机为例，提出了一种模拟空滑迫降的飞行试验方法。

1 无动力空滑参数计算

飞机空滑迫降过程可以分解为无动力直线下滑和无动力转弯两个过程。

对于无动力直线下滑，应尽可能使用最大空滑比，即单位垂直高度损失能获得的最大水平飞行距离，确保飞机尽可能滑至机场。因此，首先必须确定飞机的最佳空滑比和下滑速度。

对于无动力转弯下滑，应在已确定的下滑速度下，使180°转弯的高度损失尽可能小，同时满足飞行员视场和操纵要求。因此，需要确定飞机的转弯坡度、转弯半径及180°转弯的高度损失。

1.1 无动力直线下滑参数计算

飞机直线下滑时的纵向运动平衡方程为：

式中，P 为发动机推力，θ 为轨迹倾角，D 为阻力，L 为升力，α 为迎角，φp为推力作用线与飞机迎角基准线之间的夹角。发动机停车后推力为零，根据式（1）可得停车后的空滑比：

最佳空滑比和下滑速度确定方法为：给定飞机下滑速度，通过飞机的纵向运动平衡方程求出各速度下的升阻比，即空滑比，对比得出最佳空滑比，以及最佳空滑比对应的下滑速度。

某型飞机在空中出现发动机停车时，其襟翼偏度存在两种状态，分别对这两种状态进行计算，空滑比随表速变化曲线如图1 所示。由图1 可知，两种状态的最佳空滑比分别为6.77 和9.19，对应的表速和下滑轨迹倾角分别为330km/h、370km/h 和9.4°、6.8°。

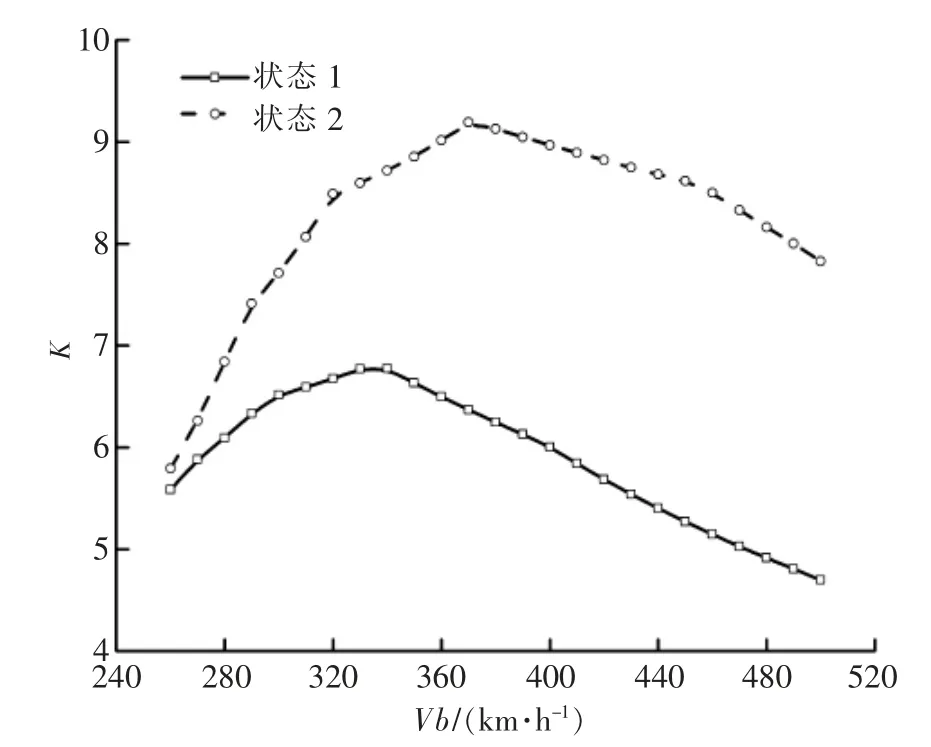
图1 空滑比随表速变化曲线

1.2 无动力转弯参数计算

转弯过程可近似认为稳定盘旋下降过程，其运动方程[4]为：

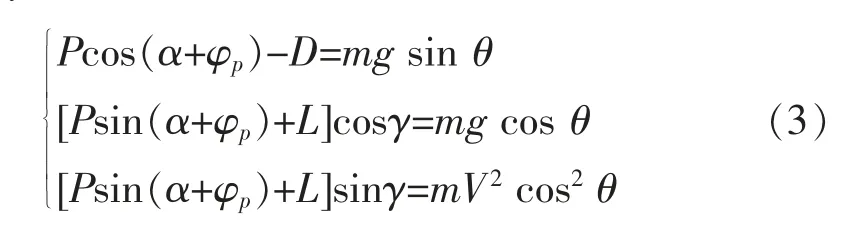
式中，γ 为坡度，R 为半径。

下降速率：Vy=Vsinθ；

一般情况下，飞机在空滑过程中，会采用直线下滑段的下滑速度进行转弯。采用已确定的空滑速度，给定转弯坡度γ，通过运动方程，即可以求出无动力转弯180°过程各参数，可以得到高度损失最小的坡度。最终将转弯坡度确定，还需要考虑到飞行员视角和驾驶技术难度，并兼顾高度损失。

不同坡度下转弯180°损失高度如图2 所示，根据计算结果可以得到，高度损失最小的坡度应在50°～55°。但是考虑到飞行员视角和驾驶技术难度，并兼顾高度损失，最终将转弯坡度确定为30°[5]，两种状态下转弯180°损失高度分别为967m 和883m。

图2 不同坡度下转弯180°损失高度

2 空滑迫降的模拟方法

2.1 空滑迫降的模拟原理

空滑迫降的物理描述可视为飞机失去动力后在飞行员的操纵下进行着陆的过程，整个过程相对于飞机的运动特性来说是一个长时间尺度的运动过程。因此，飞行员在操纵飞机进行空滑迫降时主要关注的是慢变量即飞行高度、飞行速度和运动轨迹等，而不太关注飞行迎角、俯仰角等快变量[1]。

在飞行试验中，我们可通过调整发动机油门，并配以打开减速板增加阻力的方式使得飞机的模拟空滑迫降的下滑轨迹与其无动力空滑迫降的下滑轨迹保持一致，进而保证其他空滑迫降关键参数如180°转弯损失高度等也保持一致。即可认为该次飞行试验较好地模拟了飞机无动力空滑迫降的过程。

2.2 模拟空滑迫降策略

考虑到发动机慢车时实际有一定推力，而且发动机停车后还存在额外的风车阻力，因此一般采用放减速板抵消发动机推力、模拟风车阻力的方式进行模拟空滑迫降验证。在飞机构形相同时，模拟空滑迫降接近真实发动机停车后的无动力空滑迫降的条件是，减速板的阻力减去发动机慢车推力，近似等于发动机停车后的风车阻力。

某型飞机减速板的阻力、发动机慢车推力和发动机停车后的风车阻力间的关系如图3 所示，由于减速板的阻力系数较大，减速板的阻力减去发动机慢车推力，仍远大于发动机停车后的风车阻力。因此，在飞机构形相同时，采用放减速板的方式不能模拟真实空滑迫降。

图3 减速板的阻力、发动机慢车推力和停车后的风车阻力间的关系

某型飞机，由于发动机停车后，前后襟翼不能正常偏转，处于故障状态。其中，在正常情况下，其襟翼无法偏至和状态1 相同的偏度。在模拟空滑迫降时，还存在因构形带来的升阻特性的差异，如图4 所示。仅通过判断减速板的阻力、发动机慢车推力和停车后的风车阻力间的关系，不能确定其是否能模拟真实空滑迫降。因此，需要通过对模拟空滑迫降的 “空滑比” 进行计算，通过与无动力空滑迫降的空滑比进行计算，来判断其是否能模拟真实空滑迫降。

模拟空滑飞机下滑速度取无动力空滑的下滑速度，求出慢车状态下的 “空滑比” 。取发动机推力为慢车状态推力，根据式（1）可得 “空滑比” ：

图4 状态1 发动机停车与模拟空滑时两种构形升阻差异

根据无动力空滑计算确定的飞机最佳空滑比对应的下滑速度，插值出飞机慢车推力，通过飞机的纵向运动平衡方程求出对应的 “空滑比” 。

某型飞机不同状态下，模拟空滑与真实空滑的 “空滑比” 对比如表1 所示。由于减速板的阻力系数较大，减速板的阻力减去发动机慢车推力，仍远大于发动机停车后的风车阻力，因此对于状态2，模拟空滑的 “空滑比” 远小于真实空滑的空滑比。采用放减速板的方式不能模拟状态2 的真实空滑迫降，若需要模拟，可采用增加发动机推力的方式。对于状态1，模拟空滑的 “空滑比” 接近真实空滑的空滑比，可以采用放减速板的方式进行模拟。

表1 模拟空滑与真实空滑的 “空滑比” 对比

2.3 飞行试验验证

基于本文所建立的空滑迫降模拟方法，以某型飞机为对象，开展了模拟空滑迫降科目飞行试验，基于飞行试验结果，计算得到了模拟空滑迫降的关键参数 “空滑比” 与 “转弯180°损失高度” ，并将其与理论无动力空滑迫降的空滑参数进行了对比。对比结果如表2 所示。

表2 模拟空滑飞行试验结果

由表2 可知，对于状态1，采用发动机慢车并打开减速板的方法进行了模拟空滑迫降飞行试验。通过飞行试验计算的模拟空滑比、转弯180°损失高度与理论计算得到的基本一致，且与无动力空滑迫降的关键参数误差较小。对于状态2，分别采用了 “发动机慢车并打开减速板” 与 “发动机0.3 最大并打开减速板” 的方法开展了模拟空滑迫降飞行试验。结果表明，采用发动机慢车方法时，虽然通过飞行试验计算得到的空滑关键参数与理论模拟空滑关键参数结论基本一致，但与理论无动力空滑迫降关键参数有较大的差异，而加大推力后，通过飞行试验与理论计算得到的模拟空滑参数与无动力空滑参数误差保持在2%内。

上述试验结果与理论计算的对比也即证明了本文所提出的模拟无动力空滑迫降方法是正确可行的。

3 结 论

本文以某型飞机为例，通过对无动力空滑迫降参数和模拟空滑 “空滑比” 的计算与对比，分析了对于某型飞机采用放减速板的方式进行模拟空滑迫降飞行试验的可行性。试验结果表明：某型飞机停车后，存在两种构形状态，对于状态1，采用慢车放减速板模拟空滑迫降的方式可行；对于状态2，采用慢车放减速板模拟空滑迫降的方式不可行，若要模拟，需增加发动机推力。