城镇居民消费函数的构建

林昊琦

摘 要：本文利用OLS构建我国城镇居民消费水平与城镇居民家庭人均收入、城镇居民消费者信心指数、就业率之间的回归关系，并进行拟合优度、参数显著性及计量经济的几个基本假设检验，最终得到城镇居民消费函数模型。

关键词：OLS;消费水平;人均收入;消费者信心指数;就业率

一、引 言

自改革开放以来，随着经济的迅猛发展，人们的消费水平也得到了改善，消费已经成为拉动我国经济增长的“第一动力”。由此可见，对消费水平的预测也尤为重要。

消费者信心指数是指消费者依据国家或地区的经济发展形势，对就业、收入、物价、利率等问题的综合判断后得出的一种看法和预期，由消费者满意指数和消费者预期指数组成[1]。其可以综合反映出消费者对收入、宏观经济、就业状况、生活质量、消费支出等方面的预期情况及满意程度，直接反映出消费者对未来经济活动的期望，从而影响当前的消费水平。因此，在消费函数模型中引入消费者信心指数这一变量有很大的意义。

于是，本文选取城镇居民消费水平（Y）作为解释变量。同时考虑到居民目前是否就业，是否有收入，收入的多少等因素对消费水平的影响，本文选取以下三个变量：城镇居民家庭人均收入（X1）、城镇居民消费者信心指数（X2）、就业率（X3）来衡量城镇居民消费水平（Y）。

二、數据的获取及预处理

为了研究消费函数的模型，我们选取1999年～2017年的数据作为研究对象，并从中国统计年鉴获取该时间内Y、X1、X2及X3的值。由于变量之间数值差异较大，本文便使用如下公式对数据进行指数化处理，消除变量间的量纲关系。

三、模型的建立及检验

通过观察样本数据，发现Y与X1、X2及X3之间存在一定的线性关系，可以建立多元线性回归模型。于是我们初步设置如下模型：

接下来，我们利用OLS对模型参数进行估计，得到如下方程：

从拟合效果来看，说明方程拟合优度很好。同时，变量系数通过了F检验及t检验，说明一定显著性水平下，这个模型是有意义。接下来，我们对违背基本假设的几种情况进行检验。

1.多重共线性检验

多重共线性的存在，会使得参数的估计量非有效，参数估计量的经济意义不合理，参数的显著性检验失去意义及模型的预测功能失效。

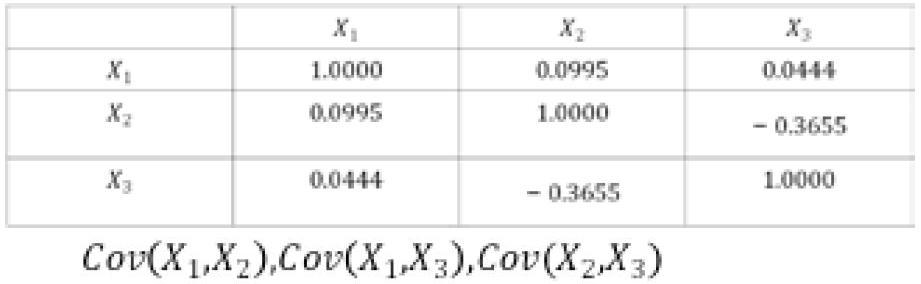
于是，我们通过计算协方差，检验变量之间是否存在相关性，得到如下结果：

的值都远小于1，说明变量之间两两不相关，即该模型不存在多重线性相关性。

2.序列自相关性检验

序列相关，会导致OLS估计量不再具有有效性。于是我们利用D.W.检验序列是否存在自相关性，得到如下结果：

说明序列不相关。

3.异方差检验

模型一旦出现异方差，会导致参数估计不再有效，变量的显著性检验失去意义，模型预测失效等后果。于是，我们利用怀特（White）检验，得到obs*R-square及F-statistic的p值均大于0.05，说明在5%的水平下，我们接受同方差的假设。

4.平稳性检验

为了确定变量数据没有随机趋势，排除“伪回归”问题，我们采用ADF检验序列的平稳性。我们得到X1、X2及X3的t-statistic的p值均小于0.05，说明不存在单位根，即该序列是平稳时间序列。

结 论

通过拟合优度、参数显著性及基本假设检验的结果可知，我们构建的模型是有效的。从经济意义上看，随着人均收入及就业率的增加，居民的消费水平也会随之增加。由于收入的波动往往和信心指数波动同步，但消费的波动相比之下会更小。所以当经济发展前景好时，消费没有同步跟上去，使得信心指数与消费呈现反向关系，这也是信心指数系数小于0的原因。综上分析，模型的参数符合实际意义。因此，该模型能较好的反映城镇居民的消费情况。

参考文献

[1] 李明，黄珊燕，张琦.我国消费者信心指数与消费函数之间的关系研究[J].统计与决策，2011（09）：110-112.