OFDM系统中深度神经网络指导的IQ不平衡补偿算法

刘思琦,王天宇,王少尉

(南京大学 电子科学与工程学院， 江苏 南京 210023)

同相正交(In-phase and Quadrature-phase，IQ)不平衡存在于系统的收发端两侧，可以分为与频率无关的和与频率相关的IQ不平衡，分别由振荡器和滤波器的非理想特性产生，这种非理想特性导致I、Q两路上的信号在幅度和相位上产生不同程度的失真[1]。对正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统来说，与频率无关的IQ不平衡对于不同频率子载波信号造成的失真是确定的，它会导致星座点的扩散和相位的旋转。具体表现为，在时域信号中引入了原始信号的共轭项干扰，即镜像干扰；在频域上，该共轭干扰表现为镜像子载波[2]。而与频率相关的IQ不平衡对不同频率的子载波信号产生不确定的失真，导致在同一星座点上的信号产生不同程度的扩散和相位旋转。它所产生的干扰在频域上表现为多个其他子载波信号干扰的叠加。这种干扰使得子载波间的正交性被破坏，接收信号无法正常解调，严重影响了系统性能。为了解决这一问题，需要对IQ不平衡进行估计和补偿。本文主要关注与频率无关的IQ不平衡的估计与补偿。

传统的与频率无关的IQ不平衡补偿方案可以分为自适应的方案和基于训练序列(导频)的方案。文献[3]提出了一种自适应的估计方法，它将I、Q两路的不平衡等效到Q路上，然后在接收端的Q路设计一个自适应滤波器，来对IQ不平衡进行估计和补偿。文献[4]提出了一种在频域上利用自适应滤波器的补偿方法，它可以估计每个子载波上的IQ不平衡和对信道的影响。文献[5]利用训练序列的频域结构，对IQ不平衡和信道进行联合估计。文献[6]设计了一种特殊的训练序列结构，同时估计收发两端的IQ不平衡。文献[7]联合考虑了IQ不平衡和相位噪声的影响，先从频域获得的IQ不平衡和相位噪声的影响参数中分离出IQ不平衡的参数；然后在时域对信号做IQ不平衡补偿；最后再回到频域，并对IQ不平衡补偿后的信号做相位噪声的估计和补偿。

深度学习作为机器学习的重要分支，在各个领域(如自然语言处理、计算机视觉等)取得了巨大的成功。它不依赖于有严格数学表达的模型，可以仅凭训练数据生成模型[8-9]。近年来，由于深度学习技术的发展加强了机器学习的计算能力，应用机器学习方法解决无线通信系统问题再次引起了通信专家的注意，许多与深度学习相关的技术也已经被应用到无线通信系统的物理层解决方案中来[10]。文献[11]提出了一种新的基于自编码网络的高峰均比抑制技术，它能更高效地抑制OFDM系统中峰均比过高的问题。文献[12]提出了一种联合信道估计和信号探测的深度神经网络算法，相对于传统的最小均方误差(Minimum Mean-Square Error, MMSE)和最小二乘(Least Squares, LS)估计算法，取得了较好的误码率(Bit Error Ratio, BER)性能。由于不需要依赖精确的数学模型，文献[13]证明了深度学习在处理硬件损伤问题时，相对于传统算法有较大优势。

本文提出了一种基于深度神经网络的IQ不平衡估计和补偿算法，采用并联的网络结构，并利用干扰来自镜像子载波的先验知识对网络进行初始化，该算法可以直接将信号从接收信号的频域形式恢复为原输入信号的二进制序列。以误码率性能作为评估标准，对比了本文所提算法和传统的LS补偿算法的性能。仿真结果表明，本文算法在幅度和相位失真的补偿效果上均优于传统算法，证明了所提算法的有效性。同时，本文还对比了完全数据驱动和模型驱动的深度神经网络算法的补偿性能，在信噪比(Signal-to-Noise Ratio, SNR)大于15 dB的情况下，模型驱动的算法误码率更低，证明了模型驱动的深度神经网络的优越性。

1 系统模型

本文假设在只有发射端存在与频率无关的IQ不平衡，在OFDM系统中，与频率无关的IQ不平衡是由IQ两路的混频器在幅度和相位上的偏差引起的。图1给出了发射端存在与频率无关的IQ不平衡时的系统模型。

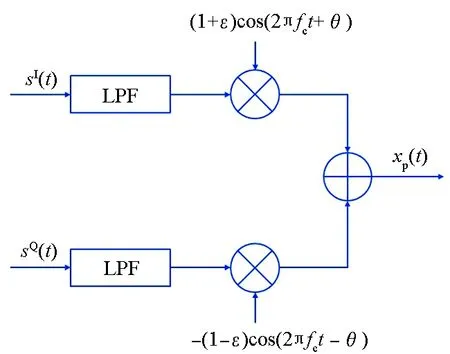
图1 发射端存在IQ不平衡时的系统模型Fig.1 System model of transmitter with IQ imbalance

图1中：ε和θ分别为幅度不平衡和相位不平衡参数；sI(t)和sQ(t)分别为I、Q两路发送端数据的时域形式；xp(t)为发射的带通信号，其等效低通信号为x(t)。根据图1，可以得到：

xp(t)=sI(t)(1+ε)cos(2πfct+θ)-

sQ(t)(1-ε)sin(2πfct-θ)

=xI(t)cos(2πfct)-xQ(t)sin(2πfct)

(1)

其中：

xI(t)=sI(t)(1+ε)cosθ+sQ(t)(1-ε)sinθ

(2)

xQ(t)=sI(t)(1+ε)sinθ+sQ(t)(1-ε)cosθ

(3)

则发射端受到IQ不平衡影响的信号x(t)与原信号s(t)有如下关系：

x(t)=as(t)+bs*(t)

(4)

其中：

a≜cosθ+jεsinθ

(5)

b≜εcosθ+jsinθ

(6)

假设在OFDM系统中，有N个子载波，用FH表示傅里叶逆变换，得到：

s=FHS

(7)

s*=conj(FHS)

(8)

式中，conj(·)表示共轭。

可以得到接收端接收到的受到IQ不平衡影响的信号经快速傅里叶变换(Fast Fourier Transform, FFT)后的频域表达式为：

Y=HX=H(aS+bS*)=H(aS+bFconj(FHS))

(9)

为方便表达，令Z=Fconj(FHS)。对于发送信号S=[S1,S2,…,SN]T，其共轭项干扰在频域上对应的镜像子载波与原信号在频域上的形式有如下对应关系，即第k个子载波传输的时候，接收到的信号是第k个子载波和第(N+2-k)个子载波上信号的叠加，如式(10)所示：

(10)

联立式(9)～(10)，得到化简后的接收信号频域表达形式为：

Yk=aHkSk+bHkZk

(11)

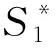
2 并联深度神经网络补偿算法

本文提出了一种基于深度神经网络的补偿算法，直接将频域接收信号恢复成原发射信号的二进制序列，即接收机的快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)解调器的输出与训练好的神经网络的输入直接相连，神经网络的输出即为待恢复的原二进制序列。其中，深度神经网络采用并联的网络结构，以降低网络优化的计算复杂度，各并联子网络均为全连接的深度神经网络(Fully Connected Deep Neural Network, FC-DNN)。图2所示为一个5层的FC-DNN，各层神经元个数为2N、4N、4N、4N、mI。其中：N为子载波数，其输入层神经元个数为2N，输入数据为接收端所有子载波上信号频域表达式的实部与虚部；I为当前网络估计补偿的符号所对应的子载波个数；m为调制阶数。每m个神经元对应一个原输入信号的调制符号，则输出层共mI个神经元，依次对应输入I个调制符号的二进制序列。由此得出，每个子网可以估计补偿I个并行子载波上符号的IQ不平衡失真，则共需要K=N/I个并联的子网络。在一次训练过程中，子网络共用一个样本，其输入均为接收信号的频域形式，标记则为各子网络对应的子载波上原输入信号的二进制序列，该对应形式可以是随机的，也可以是按照规则设定的。

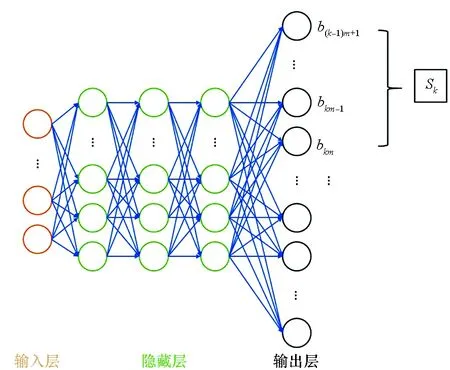
图2 并联深度神经网络的子网络结构Fig.2 Structure of subnet of parallel DNN

本文提出的补偿算法分别训练了完全数据驱动和模型驱动的深度神经网络结构。完全数据驱动的深度神经网络可以只利用数据训练生成模型[14]，它使网络不依赖于有严格数学表达的模型，在处理一些难以建立精确数学模型的问题(如通信中复杂场景下的信道建模问题，或者硬件损伤问题)时，能获得更好的性能。而模型驱动的深度神经网络可以利用特定领域中成熟的先验知识对网络进行初始化[15]，从而加快网络优化的收敛速度，进一步提高系统性能[16-17]。

上述两种算法的区别在于，是否引入了有效的先验知识对网络进行初始化，在本文算法中，网络的初始化主要体现在各子网络的输出层神经元对应补偿的符号所在的子载波Sk是否按照先验知识分布。对完全数据驱动的深度神经网络来说，各子网络对应的Sk是随机的，并联的网络结构只是降低了网络优化的计算复杂度。

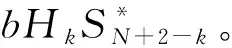
3 仿真与分析

本文考虑在OFDM系统中，采用8 PSK调制。子载波数N=32，每个小批量样本数据集的样本数SN=128。则每SN·N个符号作为原信号的一帧。信道采用一般的多径信道，并加入高斯白噪声。多径信道径数为4，延迟分别为0、3、4、7，单位为采样点；各径对应的能量分别为-3.979 4dB、-3.979 4dB、-6.989 7dB、-10 dB。在训练开始前，将生成的数据集分为三部分，其中3/5为训练集，1/5为验证集，1/5为测试集。

对应的并联深度神经网络由4个子网构成，每个子网采用相同的结构，各自对应8个子载波上信号的估计补偿。网络采用动量随机梯度下降优化算法和均方根误差损失函数，其具体训练参数如表1所示。其中，输出层对应估计补偿的子载波对于所提两种算法略有不同。对于完全数据驱动的深度神经网络模型，输出层神经元对应的Sk按顺序计，它的训练标记为对应子载波上发送符号的频域形式[S8(n-1)+1,…,S8n]所对应的二进制序列。

表1 神经网络训练参数

模型驱动神经网络的输出层考虑将自身镜像的S1、SN/2+1放在一个子网中，各子网络对应规则如表2所示。

表2 模型驱动网络各子网输出神经元设置

仿真结果如图3所示，图中给出了LS算法和本文算法的误码率性能对比，其中IQ不平衡参数θ=15°，ε=0.1。从图中可以看出，在不使用任何补偿算法的情况下，误码率不随信噪比的增加而变化，此时接收信号无法被正常解调。对比提出的补偿算法和LS算法，所提算法在所有信噪比的情况下，均得到了更好的误码率性能。随着信噪比的增加，误码率下降的优势更加明显，在SNR为20 dB的情况下，本文算法的误码率较传统算法降低了一个数量级。对比完全数据驱动与模型驱动神经网络的误码率性能，可以看出，在SNR低于15 dB的情况下，两种算法的性能相似；在SNR高于15 dB的情况下，模型驱动的算法误码率性能更好，并且随着SNR的继续增加，优势逐渐增加。

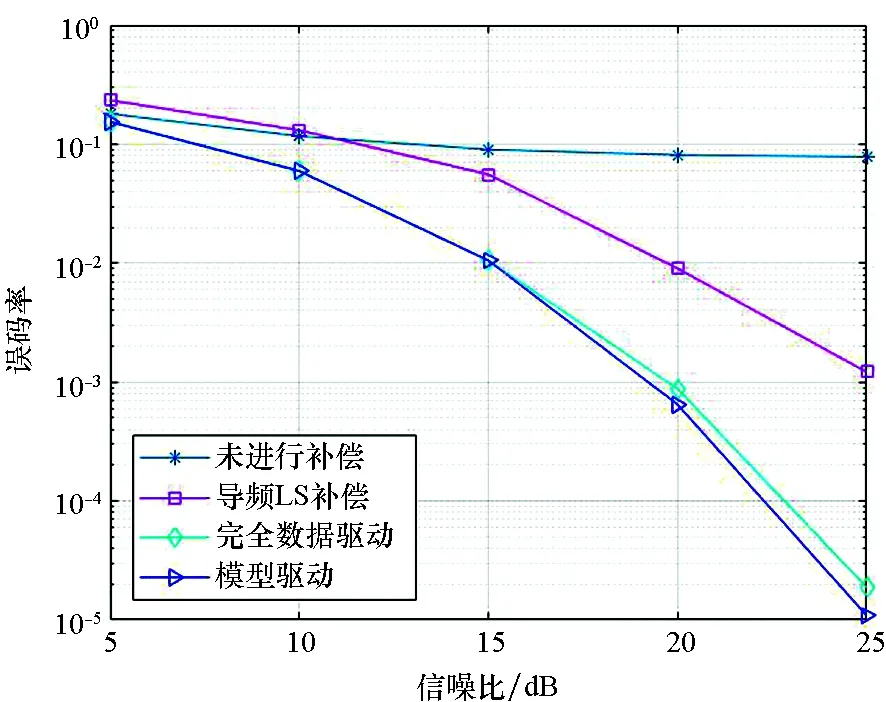
图3 不同算法的误码率性能(θ=15°，ε=0.1)Fig.3 BER performance of different IQ compensation algorithms(θ=15°，ε=0.1)

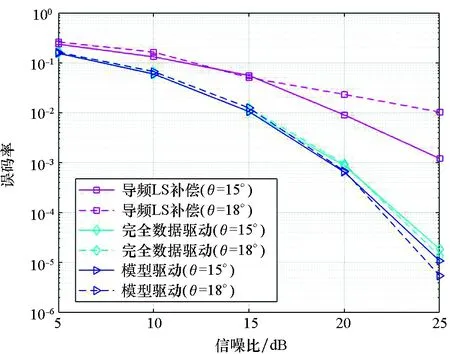
图4 相位不平衡参数增大对误码率的影响(ε=0.1)Fig.4 BER performance comparison with larger phase imbalance parameter(ε=0.1)

图4给出了在相位不平衡参数增大后，各补偿算法得到的BER性能对比图，其中相位不平衡参数变为θ=18°，在图中均以虚线表示；对照组相位不平衡参数为θ=15°，在图中均以实线表示。同时幅度不平衡参数保持为ε=0.1。从图4中可以看出，相位不平衡参数增加3°后，基于导频的LS补偿算法的误码率性能明显恶化，在SNR为25 dB时，其误码率变化从10-3降至10-2，减小了一个数量级。而所提出的两种算法，其误码率性能基本保持不变。这说明了所提算法对于相位不平衡的补偿效果要优于传统算法。

此外，还对比了增大幅度不平衡参数后各补偿算法的BER性能，如图5所示。图中给出了幅度不平衡参数分别为ε=0.1(实线)和ε=0.12(虚线)时的误码率性能对比，此时相位不平衡参数均为θ=15°。从图中可以看出，幅度不平衡参数增大对各算法的误码率性能影响较小，其误码率性能变化可以忽略。对比图4和图5可以得出，OFDM系统对相位不平衡参数的变化更加敏感。

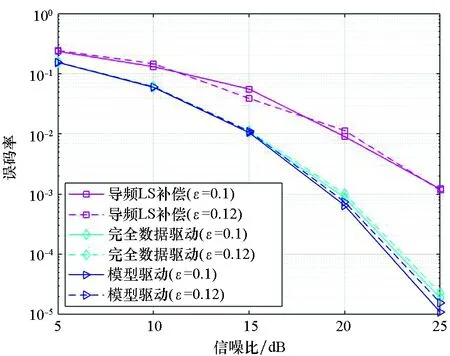
图5 幅度不平衡参数增大对误码率的影响 (θ=15°)Fig.5 BER performance comparison with larger amplitude imbalance parameter (θ=15°)

4 结论

本文考虑了OFDM系统中发射机存在与频率无关的IQ不平衡问题，提出了一种并联深度神经网络架构下的IQ不平衡补偿算法。该算法利用深度神经网络不需要精确数学模型的特点直接恢复原信号的二进制序列，同时，结合IQ不平衡干扰会造成镜像子载波叠加的先验知识对网络进行初始化。仿真结果表明，该算法能有效地对IQ不平衡进行补偿，并且其误码率性能优于传统基于导频的LS补偿算法。另外，通过对比模型驱动的深度神经网络算法和完全数据驱动算法的误码率性能，验证了模型驱动的深度神经网络更适用于无线通信中物理层的解决方案。仿真结果还表明，在幅度和相位不平衡参数进一步恶化后，相较于传统算法，所提算法的补偿效果能继续保证较好的误码率性能。