数学建模在初中数学教学中的应用

福建省漳州市龙海莲花中学 何继芳

由于初中阶段的学生在逻辑思维方面还存在一定的不足，所以在教学中教师要及时更新教育思想与方法，提升学生学习能力，帮助学生掌握数学知识点，发挥数学建模作用，在简化数学问题的同时促进学生掌握解题技巧，从而提高学习效果。

一、初中生数学建模中存在的问题

研究发现，目前一些初中生表现出了数学建模素养不高的现象，尤其是在分析问题、解决问题能力等方面存在一定的不足。所以在教育教学中，教师要找出学生出现这一现象的原因，做好转变工作。首先，一些学生心理方面存在一定的障碍。由于数学知识有着抽象性与逻辑性较强的特点，很容易让学生对数学知识产生戒备心，甚至表现出自信心不足等现象，在面对数学知识时也就会产生厌烦的心理。其次，一些学生存在思维局限性现象。初中数学问题复杂程度增加，需要学生找出相应的数量关系，以抽象思维来解决问题。但是由于一些学生的直接思维能力与抽象思维能力不足，影响了他们对数学知识的理解，影响了学生建模能力的提升。最后，学生在数量分析方面存在一定的不足。受基础知识的限制，数量关系、数形结合等很容易对建模产生直接的影响，最终也会影响到学生的学习效果。

二、在初中数学教学中应用数学建模的措施

（一）启发学生建模思想

由于数学知识有着抽象性与逻辑性较强的特点，所以一些学生在学习中表现出了许多的问题。因此，教师就要利用数学问题来培养学生的自主学习能力，鼓励学生进行实践探索，在帮助学生掌握数学现象的同时提出自己的问题，通过准确分析与研究来解决问题，形成建模思想。所以，培养学生问题意识已经成了建模思想形成的关键所在。教师也要及时为学生构建适宜的教学情境，让学生主动探索数学知识。首先，营造学习环境。由于这一阶段学生思维比较活跃，能够对新鲜事物产生浓郁的好奇心，所以教师要利用学生这一特点，向学生提出实际问题，锻炼学生问题意识。在传统教育模式中，许多学生处于被动学习状态，加之课堂互动性不足，影响到了学生的学习效果。但是在现代数学教学中，教师则要从营造学习环境出发，清楚认识到学生才是课堂中的主体，自身则要以引导者的身份来帮助学生学习，激发学生探索欲望。其次，营造问题环境。当学生置身于良好的学习环境时，往往能够产生问题意识，从而也就可以积极参与学习，在问题情境中找出数学知识点。因此，在创建问题情境时就要结合学生的生活实际，引入趣味性数学故事，鼓励学生提出具体问题，在引导学生探索中找出解题方法。

（二）数学建模在教学中的运用

我们的日常生活中随处可见数学，数学在实际生活中运用广泛，教师应培养学生具有数学建模的思想。学生通过一些具体实例实践、分析、归纳，将所学知识渗透到实际问题中，才能初步形成数学建模能力，建立数学模型，解决实际问题。

1.在几何上的运用

在几何中测量一些高大物体的高度，如东方明珠塔、金字塔的高度以及河岸的跨度等我们不能直接测量，可引导学生进行数学建模，运用三角形相似解决实际问题。

例如，据史料记载，古希腊数学家、天文学家泰勒斯曾经利用三角形相似的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度。如图一，木杆EF 长2 米，它的影长FD 为3 米，测OA 长为201 米，求金字塔的高度BO。

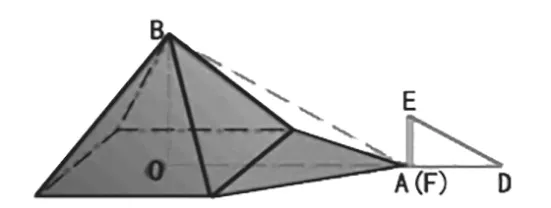
图一

图二

又如图二，为了估算河的宽度，我们可以在河对岸选定一个目标P，在河的这一边取点Q 和S，使P、Q、S 三点共线且直线PS 与河岸垂直，接着再过点S 且与PS 垂直的直线a上选择适当的点T，确定PT 与过点Q 且垂直PS 的直线b 的交点为R。如果测得QS 为45 米，ST 为90 米，QR 为60 米，求河的宽度PQ。

解：∵∠PQR=∠PST=90°，∠P=∠P

∴△PQR ～△PST

∴PQ×90=（PQ+45）×60，解得PQ=90（米）

2.在函数中的运用

日常生活中有关商品利润的最大化、旅游消费费用的最小值、建筑物的设计等问题，我们就可引导学生进行数学建模，运用一次函数和二次函数解决实际问题。

（1）一次函数模型

例如：学校有一批复印任务，原来由甲复印社承接，按每100 页40 元计费。现乙复印社表示，若学校先按每月付给200 元承包费，则可以按每100 页15 元收费。①设学校复印的页数为x，试写出甲、乙两家复印社的收费y甲、y乙与x 之间的函数关系式；②若该学校估计每月的复印页数不超过1000 页，那么学校应该选择哪个复印社复印？

解：①y甲=0.40x，y乙=200+0.15x（学生基本都能写出来）

②设问你是怎么想的？应该怎么分情况讨论呢？

（解决问题：什么时候甲、乙两复印社收费相同？什么时候甲复印社收费大于乙复印社收费？什么时候乙复印社收费大于甲复印社收费？收费相同在图像上怎样反映出来？结合函数图像探究）

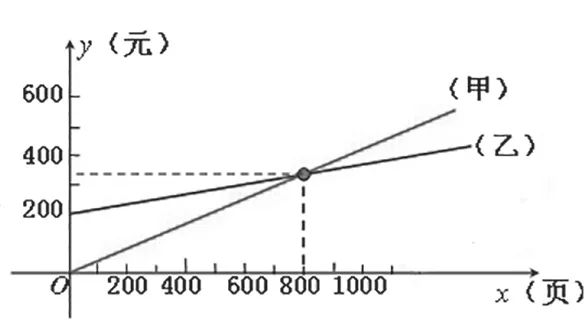
解析：当0.40x=200+0.15x，即x=800（页），学校选择甲复印社或乙复印社复印都可以；当0.40x ＜200+0.15x 即x ＜800（页），学校选择甲复印社复印支付费用比较少；当0.40x ＞200+0.15x，即x ＞800（页），学校选择乙复印社复印支付费用比较少。因此，结合实际，学校复印任务数在不多于800 页时选择甲复印社复印，复印任务数多于800 页时选择乙复印社复印。

（2）二次函数模型

例如：如图，一座拱桥的纵截面是抛物线的一部分，拱桥的跨度是4.9 米，当水面宽度是4 米时，拱顶离水面2 米。现在想了解水面宽度变化时，拱顶离水面的高度怎样变化。你能想出办法来吗？

引导学生建立函数模型。设问：这是什么样的函数呢？（拱桥的纵截面是抛物线，所以应当是个二次函数）再问：如何建立直角坐标系呢？（学生通过探究，得到如下几种坐标系建立法）

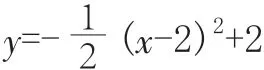
通过比较可知，以拱顶为原点，抛物线的对称轴为y 轴建立直角坐标系（如第2 个图）得到的函数表达式最简单、最合适（即y=ax2型）。

总之，针对上面几个日常生活中的实例，我们引导学生通过所学知识分析问题、建立数学模型，最后得以解决问题。

（三）培养学生符号意识

由于数学知识中存在丰富的符号内容，所以可以借助符号来表示相关数学知识，让学生在推理与分析中掌握计算技巧。在新课改背景下，要从培养学生符号意识入手，鼓励学生学习数学知识，利用数学建模将抽象的数学知识直观展现出来，发挥数学符号的作用。所以在教学中就要从建模思想入手，锻炼学生用字母表示数的能力。由于这一阶段学生受到前阶段学习的影响，对数字有着较强的依赖感，教师就要有意识地引导学生，让学生习惯运用字母来替代数量和数量的关系。

例如：A 与B 两地间隔18 公里，甲方需要在AB 之间铺设燃气管道线，乙方在AB 间铺设输油管道线。已知甲方每周比乙方少铺设1 公里，但是甲方提前3 周进行施工，最终甲方与乙方同时完成施工任务，那么甲方与乙方每周各铺设了多少公里管道线？

解：甲方每周铺设x 公里，乙方每周铺设（x+1）公里，

解得x1=2，x2=-3

经检验，x1=2，x2=-3 都是原方程的根，但x2=-3 不符合题意，舍去。

∴x+1=3，即甲方每周铺设2 公里，乙方每周铺设3 公里。

再比如，超市购物中涉及总价、数量与单价之间的关系，所以就可以借助字母表示出来，帮助学生逐渐形成字母意识。教师还可以开展符号运算训练，引入数学思想。开展符号运算训练已经成了提升学生符号意识的渠道之一，所以教师就要借助具体问题，让学生得到充分的锻炼。如在学习有理数这一内容时，一些学生很容易出现符号使用错误的现象，所以教师就可以开展强化训练，让学生真正认识符号，从而提升学生的运算能力。

（四）坚持循序渐进原则

由于长期受到传统教育思想的影响，一些教师在教学中并没有认识到建模的重要性，加之学生自身经验与能力不足，所以在学习中表现出了难以快速解决问题的现象。因此，教师在教学中要坚持循序渐进的原则，培养学生建模素养，锻炼学生学习能力。但是在教学中还要引入相关的铺垫语，让学生自行建立模型，从数量关系的角度来分析数学问题。学生只有掌握建模思想与方法，才能逐渐在学习数学知识中进行数学建模，解决相应的问题。

综上所述，初中数学教学作为学生学习中的重点与难点，将直接影响学生的后续发展。因此，教师在教育教学中就要从重视数学教学入手，以培养学生数学素养为基础，做好教学研究工作，利用建模思想来帮助学生学习，提高学生学习效果。