斜坡平台波浪破碎数值模拟
2020-08-14王红川刘华帅
王红川,刘华帅,杨 氾
(南京水利科学研究院 水文水资源与水利工程国家重点实验室,江苏 南京 210029)
波浪从深海向近岸的传播过程中,由于受到复杂地形、障碍物和水流等因素的影响,将发生浅化、折射、绕射、反射、底摩阻能量耗散以及破碎等一系列复杂现象,采用数值模拟的方法推算海岸工程中的波浪要素,波浪传播变形数学模型在理论和工程应用方面日趋成熟,已成为目前确定海岸工程设计波浪的主要手段。
近年来,随着波浪数学模型的发展和海岸工程研究需要,近岸的波浪传播至浅水区的破碎问题研究引起了很多学者的兴趣。在破碎带内,波浪能量迅速衰减,由于波浪破碎过程中的详细机理尚未完全清楚,使用较多的方法是在破碎后的波高与当地水深之间建立一种关系,“0.78”准则(破碎波高和水深之比等于0.78)提供了一种既简单、又实用的合理确定缓坡海底地形破碎波高的方法。Horikawa和Kuo[1]、Nakamura等[2]、Divoky等[3]研究认为这个准则与缓坡海岸带实际波浪破碎指标相差不大。
实际上,临界破碎波高不仅仅是波高与当地水深的简单关系,还与海底坡度、波长等因素有关。Goda[4-6]通过模型试验研究得到临界破碎波高与海底坡度、波长有下列关系:
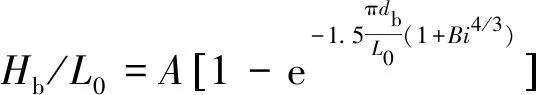
(1)
式中:db为当地水深,L0为波长,i为海底底坡,A、B为系数,通常取A=0.17,B=15,这一公式是波浪破碎的理论值,适用于任意坡度的斜坡。Svendsen[7]将波浪破碎的临界波高与波陡、当地水深等建立了关系,得出斜坡上的波浪破碎的临界波高判别标准,认为其破波公式对底坡坡度达1/3的斜坡也是适用的。
Dally等[8]总结前人的一些经验,研究了波浪在浅滩上的破碎及波浪破碎后的衰减,从控制能量平衡方程出发,建立了平底海床、斜坡海床上波浪破碎及破碎后波浪能量的衰减,得出了波浪在浅滩上破碎后的波高与传播距离之间的表达式。1978年Battjes等[9]从理论研究了斜坡海底上的随机波波浪破碎,认为波浪在海滩上破碎时,并非所有通过某一点的波高都相等,这些破后波高也不一定都比非破波波高大。他从波浪破碎后的波高分布推导出随机波在浅滩破碎时的破波概率(Qb),建立了Qb与均方根波高Hrms的关系,进一步建立波浪在破波带内的能量平衡方程,描述波浪破碎后的波高变化。Beltrami等[10]利用有限元法求解缓坡方程中的浅滩地形上的波浪破碎问题采用了这种方法,取得了较好的效果。王红川等[11]对缓坡方程进行了改进,使之适用于较陡地形上的波浪折射绕射变形计算,在此基础上自行开发研制了“波浪计算软件”,并用于长江口地区复杂地形下的波浪数值模拟计算[12-13]。
波浪在复杂地形上传播变形,在近岸浅水区斜坡地形上将发生波浪破碎,破碎后的波浪在平台上会达到一个相对稳定的状态。这里旨在从波浪破碎带内能量变化机理对波浪计算软件进行改进和完善,使之更好地应用于长江口滩槽交替等复杂地形上的波浪破碎数值模拟。
1 波浪破碎数学模型
近岸的波浪破碎是一种复杂而高度非线性的现象,缓坡方程的抛物型方程法仅限于线性或弱非线性的波浪传播模型,它不能直接描述波浪破碎的物理过程。然而基于能量平衡的波动方程可以描述波浪传播过程中的波能密度、波浪传播方向,因而在破波区近似模拟波能的衰减在一定程度上也是可行的。 Kirby和Dalrymple[14]将Dally方法应用于抛物型缓坡方程模型中,通过对岛屿附近海岸带波浪破碎现象的模拟,证明该方法是可行的。
在破波带内,波能流衰减的平衡方程可用如下方程描述:
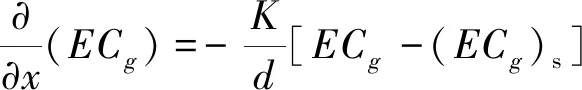
(2)
式中:d为水深;K为待定常数,与破波后波能衰减有关;(ECg)s为波浪破碎后“稳定”的能量流;E=1/8ρgH2,ρ为流体密度,H为波高;Cg=C(1+2kd/sinh2kd)/2,k、d满足弥散关系,ω2=gktanh(kd);ω=2π/T,T为波周期。这种波能耗散模型与在平底或斜坡地形上波浪传播得到的波高衰减是一致的。Dally通过对众多试验数据资料比较,表明这种分析模型对描述破波带内波浪的沿程衰减非常成功。
将式(2)改写为:

(3)
假定Cgs=Cg,Wb可写为:
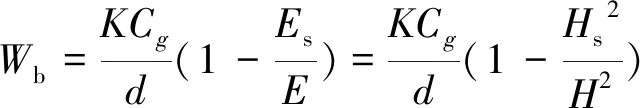
(4)
式中:H=2|A|;A为波浪振幅。破浪破碎稳定波高指标采用(H/d)s=γ,则上式可写成:
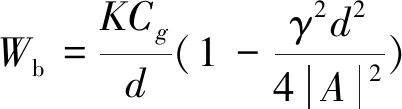
(5)
上式表达了波浪在浅滩破碎后能量流的衰减率,式中参数K、γ分别表示波浪破碎后破波带内的波浪传播衰减因子、波浪破碎后达到稳定状态的波高,这两个参数可通过模型试验得出。
另一方面,如考虑波浪在浅滩上破碎后沿x方向继续传播时的波高衰减因子与Wb的关系,将缓坡方程写为:
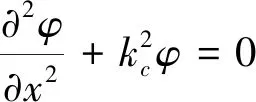
(6)
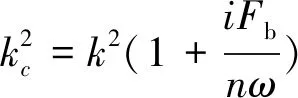
(7)
式中:Fb是波浪传播中的衰减因子。令φ=Aeikcx,A为波幅。如果将kc表示为实部和虚部,即
kc=kr+iki(i2=-1)
于是φ的指数衰减形式为:
φ=Ae-kixeikrx(ki>0)
(8)
式(8)表明波浪破碎后沿x方向传播过程中波高的衰减与传播距离有关,同时上式将波高衰减率与参数ki建立了联系。由以上关系可得出:
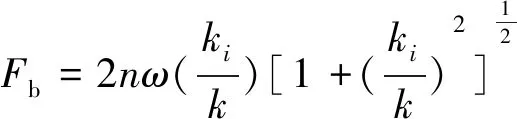
(9)
根据假定波浪破碎后波高的指数表达式,可以得出:

(10)
考虑到E=1/8ρgH2,在平底情况下上式可写成:

(11)
比较上式与式(3),可得:

(12)
Dally通过对众多试验数据资料比较,详细分析了不同海底坡度情况下的破波后的衰减因子(K)和破波后的稳定波高因子(γ),认为对于海底坡度变化较宽的范围内可采用K=0.15,γ=0.40。
2 波浪传播数学模型
如将波动方程写成非线性、考虑破波能量衰减的缓坡方程[15]:
(CCgφx)x+k2CCgφ+Mφ=0
(13)
Mφ=(CCgφy)y+(-ω2k2D|A|2+iωFb)φ
(14)
式中:φ为波势,k为波数,ω为圆频率,C为波速,Cg为波群速度,Mφ为算子,Fb为考虑波浪破碎的能量衰减因子,可用前面破波模型计算得出。由此导出的描述波浪在复杂地形下高阶非线性抛物型缓坡方程可写成:

式(15)可采用有限差分方法求解。计算程序中每一步检查波高是否超出临界波高,当波高超出临界波高,则波浪破碎,采用式(9)、(12)计算衰减系数Fb。采用式(15)考虑波浪破碎引起波能衰减的波浪传播变形模型可进行数值模拟。
3 模型参数确定
关于斜坡或缓坡上的波浪破碎及波浪传播变形的研究,国内外研究成果很多,Goda通过分析试验资料,给出了波浪破碎指标的经验式(1),这一公式是波浪破碎的理论值,适用于任意坡度的斜坡,其中A值的范围通常为0.12~0.18,Goda的成果最早发表于1970年,后来又做了相关研究加以完善,他的成果目前在国际海岸工程界广为使用,并被认识比较符合实际。
基于国内外斜坡地形上波浪破碎问题研究,在波浪水槽中开展了波浪在不同斜坡坡度潜堤上的传播和破碎物理模型试验[15],并对波浪在斜坡上的波浪破碎位置、波浪破碎指标、波浪破碎后平台上的破后稳定波高进行了研究,分别对规则波和不规则波在斜坡地形上的波浪传播变形、破浪破碎、波浪在潜堤堤后平台上的稳定波高进行了系列试验。
试验时,在斜坡坡脚与造波板之间布置波高仪,测量波浪要素作为深水入射波;当入射波要素满足预定要求时,观察斜坡上或平台上波浪的破碎带,并在破碎带内加密布置波高仪,测量波浪破碎波高及波浪变形,从而得到破碎位置。在破碎带之后布置波高仪,测量波浪破碎后的破后波。在破碎带与用来测量入射波高的波高仪之间布置若干波高仪,测量波浪的沿程变化。
试验采用固定水深变波高、周期进行试验,水深采用60 cm,平台水深为0.2 m。试验波高:约10 cm、15 cm、20 cm(采用3种不同的波高梯度分别进行试验,规则波采用平均波高,不规则波采用有效波高进行控制);波周期:1.2 s、1.5 s、2.0 s、3.0 s、4.0 s。
试验斜坡采用1/30、1/200及1/500三个坡度,斜坡末端布置40 cm高的平台,平台水深为0.2 m。试验断面如图1所示。
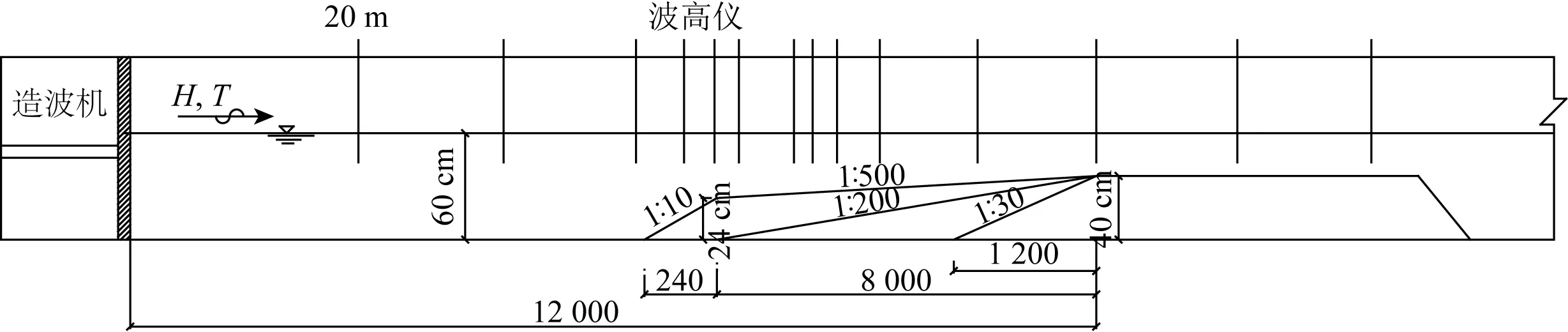
图1 模型试验断面布置Fig. 1 Arrangement of the section of the model test
通过对不同坡度上的规则波和不规则波浪在斜坡上的波浪破碎试验,分别测量了破碎波高Hb,确定波浪破碎位置和破碎水深,测量了波浪破碎后平台上的破后波高Ht。对试验结果分析表明:
1) 对于规则波可以采用Goda公式中当A=0.17,B=15时来描述不同的斜坡上波浪破碎时db/L0~Hb/L0关系的破碎指标。
2) 不规则波在斜坡上破碎时如采用波列中的最大波高Hmax作为特征波高,波浪的破碎指标也可用Goda公式中当A=0.17,B=15时来描述,也就是说不规则波波列中的最大破碎波高和规则波波高相当。
3) 波浪在浅水区域破碎后,波能迅速衰减,波浪在破波带内波高变化十分复杂,波浪在斜坡后平台上达到稳定时的波高与平台水深、斜坡坡度、波长等因素有一定的关系。破碎后的稳定波高为:
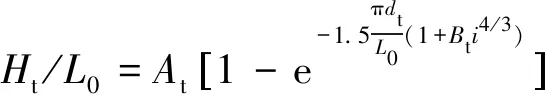
(16)
式中:dt为当地水深,参数At、Bt由试验数据拟合得出。对于规则波,At=0.09、Bt=10;对于不规则波,At=0.10、Bt=10。
4 波浪破碎数值模拟
利用前面推导的波浪破碎数学模型以及斜坡堤上波浪破碎参数可以进行波浪在斜坡堤上的传播变形数值模拟。文中数值计算采用物理模型试验[15]条件下的地形和入射波要素进行。数值模拟计算地形底坡度为1/30,斜坡顶水深为0.2 m,斜坡底部平底水深0.6 m,斜坡长度为12 m。斜坡位置及坐标见图2。起始波高分别采用22.62 cm、17.06 cm、10.48 cm,波周期为2 s。

图2 数值验证斜坡地形示意Fig. 2 The topography sketch map of the numerical test
图3分别为不同起始波高条件计算的波浪在浅滩上的波高分布以及波浪爬过浅滩在上部平台继续传播的波高沿程分布。
从图3中可以看出,波浪进入斜坡上后波高增大,在浅滩上部近平台位置或进入上部平台波浪破碎,波浪破碎后波能迅速衰减,波浪继续向前传播,直至波高达到稳定状态。几种不同波高的波浪在传播过程中,波浪破碎的位置是不一样的:前2种波浪(H0=17.06~22.62 cm)入射波高相对大些,波浪破碎位置出现在浅滩上部,距离滩顶拐角一倍波长内;当波高较小时(H0=10.48 cm),波浪在斜坡上波高增大,直至在平台上波浪破碎。由于波浪破碎,波浪在平台上传播时波高迅速减小。从数值计算与试验数据比较,前2组波浪破碎位置基本一致,破波前后的波高也十分接近,第3组的数值计算破波位置位于斜坡和平台交界处(X=0),试验结果的破波位置在平台上稍向后位置。波浪破碎后直至波高稳定的距离也较接近。
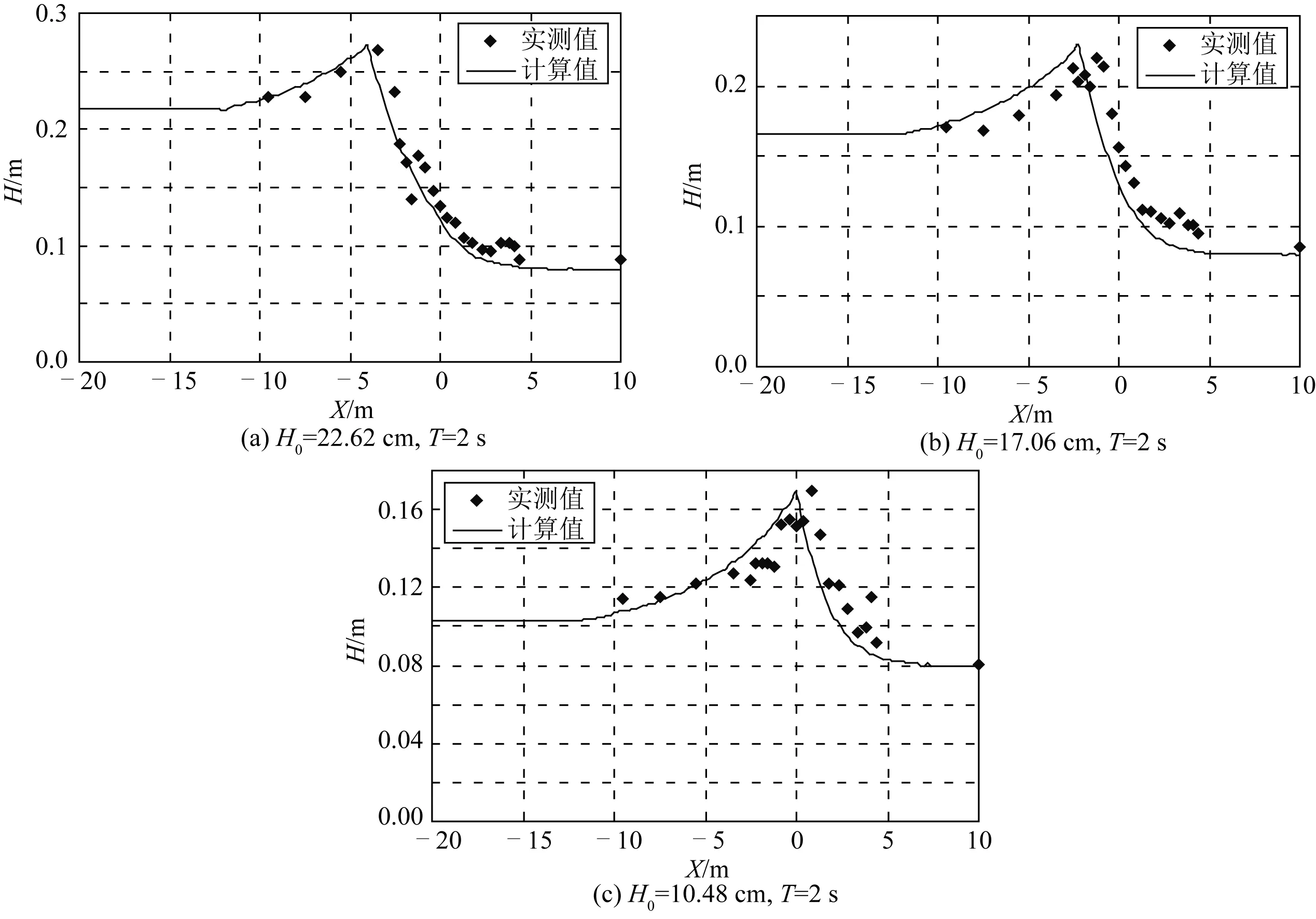
图3 不同起始波高条件下波浪在斜坡上传播波高分布Fig. 3 The wave height distribution under different start wave height
为比较波浪数值模拟的计算值和模型试验值的差异,图4给出了试验测量位置的试验波高值和计算值的比较。从图中可以看出,两者基本上是吻合的,统计表明,平均误差为2%~8%,计算值略小于试验值。
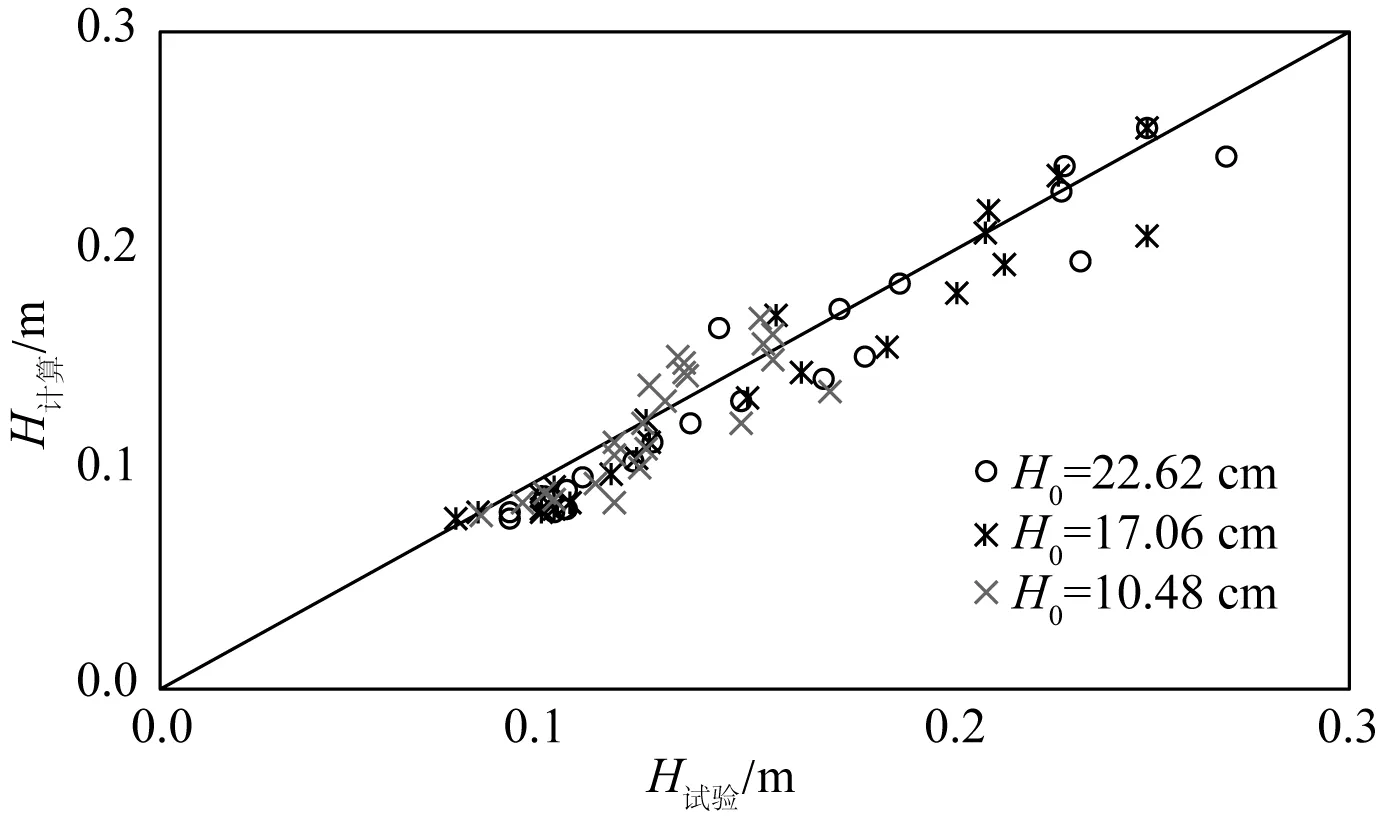
图4 不同组次波高计算值和试验值对比Fig. 4 Comparison of wave height between numerical value & experimental value
图5是将上述3组试验组次的数值计算无因次化结果与试验结果比较。图5中可知,由于底坡陡,当波浪发生破碎时,破碎波高与当地水深之比均大于0.78。
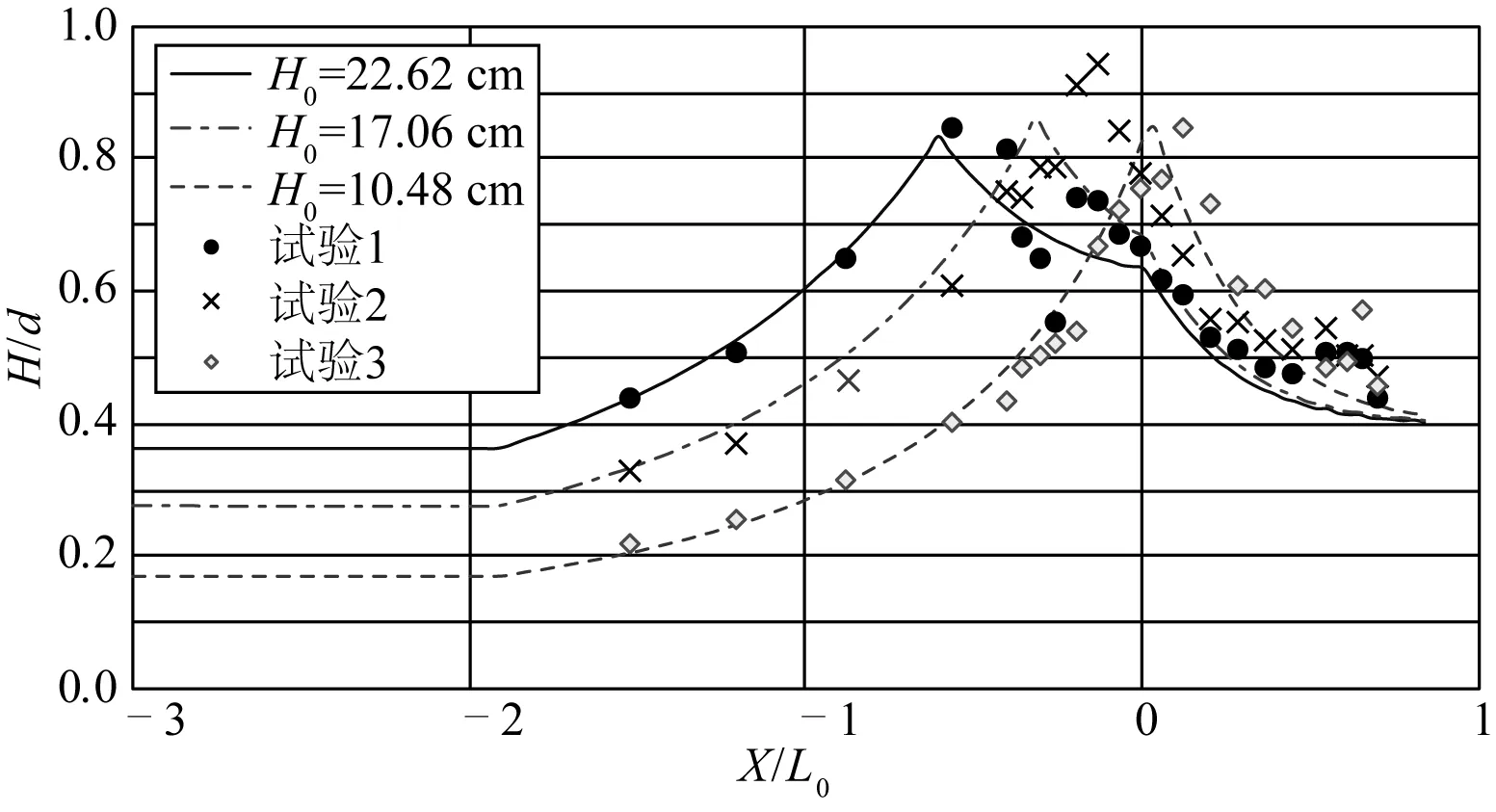
图5 无因次化波高计算值与试验值比较Fig. 5 Comparison of dimensionless wave height between numerical value & experimental value
从与试验资料的比较,可以认为本文的波浪传播变形数值计算模型可以对波浪在近岸破波带水域的波浪传播进行模拟,模拟结果是合理可信的。
5 结 语
波浪在斜坡地形上的传播变形是一个十分复杂的过程,从能量流平衡方程推导了破波带内波浪的破碎数学模型,分析了波浪在斜坡上的破碎指标和波浪破碎后在平台上的稳定波浪参数,建立了抛物型缓坡方程中描述波浪在破波带内能量衰减和波浪破碎系数之间关系,扩展波浪传播模型在近岸斜坡地形和潜堤上的传播变形数值计算。
通过数值计算和模型试验实测数据比较,文中提出的方法可以较好地模拟波浪在地形上的波高变化、波浪破碎、以及斜坡后平台上的稳定波高,计算结果和实测数据吻合较好。
