基于深度强化学习的无线网络资源分配算法*

李孜恒，孟 超

（1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2.金陵科技学院 网络与通信工程学院，江苏 南京 211169）

0 引言

随着越来越多的智能设备和物联网技术（The Internet of Things，IoTs）的广泛应用，如笔记本电脑、智能手机等，为用户提供了更加舒适的内容体验，同时导致无线流量空前增长[1]。现代无线网络正变得越来越密集化、动态化，无线通信领域面临着前所未有的挑战。绿色通信和智能网络等全新概念的提出，如何保证传输时延和用户服务体验的同时合理分配资源，实现能量效率的提高，引起了人们的广泛关注[2]。目前，传统的资源分配方法求解复杂度高、效率低，很难适应高动态性的无线网络环境，已经无法满足要求[3-4]。

随着人工智能技术的不断发展，通过数据驱动、算力驱动的深度机器学习方法可以有效解决各类问题[5]。深度强化学习是机器学习领域的重要分支，可以有效解决庞大的状态空间带来的高昂计算需求，加强算法对未知环境的学习能力。深度学习利用多层神经网络，从复杂高维的原始数据中模拟人脑进行准确的特征提取，凭借其优越的性能，逐渐成为构建具有复杂拓扑的大规模智能网络的强有力工具[6]。

由于节点的移动性、信道的变动以及相互之间的干扰，如今的无线网络受诸多因素影响，正变得十分复杂多样。相对于传统的机器学习方法，深度学习在无线网络中有着更大的潜力，具有更高的预测准确度，且无需对输入数据进行预处理，直接使用从网络中采集的特征进行训练，降低了模型复杂度。将深度学习与强化学习结合，在动态学习过程中，将所获得的历史经历存储作为神经网络的训练数据，利用深度学习的强大优势，有效提高强化学习算法的学习速度和决策性能。

本文设计了一种基于深度强化学习的复杂动态无线网络资源分配算法，可以在复杂的未知环境下，自主选择行为、制定决策并不断优化，最终得到接近最优的功率和信道分配策略。

1 系统模型

考虑动态多节点、多信道以及多功率分配问题，假设通信网络中有M个节点和N个通信链路，节点随机分布在无线网络中，如图1所示。假设m={1,2,…,M}表示节点的集合，L={ll,l2,…,ln}表示通信链路的集合，C={cl,c2,…,cj}表示可用信道的集合，P={pl,p2,…,pk}则表示可用功率的集合。为了提高能量效率，智能体将动态分配可用信道和功率给每个通信链路。

由于在通信过程中，相同频率下可能存在多条通信链路，通信链路的接收端会受到来自其他链路的信号干扰，进而影响信道容量和能量效率。因此，一条链路的容量可以由信号与干扰加噪声比（Signal to Interference plus Noise Ratio，SINR）表示：

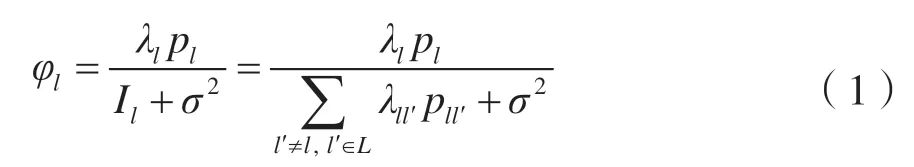
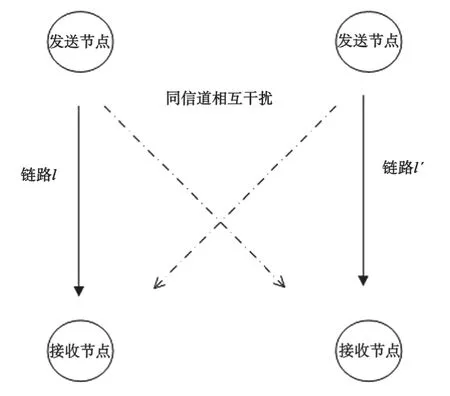
图1 同频信道内不同链路之间的信号干扰

其中，λl、pl、Il、σ2分别表示通信链路l的信道增益、传输功率、同信道信号干扰和噪声功率。基于简化的路径损耗模型[7]，接收信号受传输距离和多径衰落影响，可以将通信链路l的信道增益表示为λl=dl-δ，dl为链路l的发送节点和接收节点之间的距离，δ为路径损耗指数。同样，当通信链路l和l´在同一信道内时，同信道干扰增益可以表示为λll´=dll´-δ，dll´为l´的发送节点和l的接收节点之间的距离。因此，根据香农定理可以将链路l可容纳的最大传输速率表示为：

定义能量效率EE为：

2 基于深度强化学习的资源分配算法

强化学习是机器学习领域解决问题的重要工具，广泛用于处理马尔科夫动态规划问题[8]。如图2所示，在强化学习的过程中，智能体通过和环境交互来学习最优的策略。

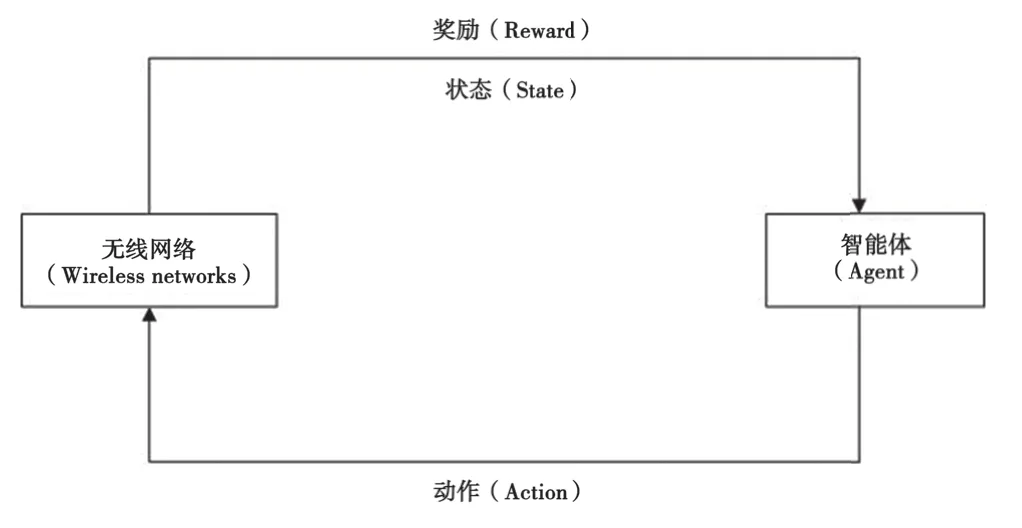
图2 无线网络环境下的强化学习

智能体观察当前状态，按照既定策略采取动作，最后收到即时回报和最新的状态，并对策略进行优化调整。智能体将重复这一过程直到最终获得最优策略。在强化学习中，Q学习是一种十分有效的方法，在学术研究中得到了广泛应用[9]。Q学习的目标是寻找最大化长期累积折扣回报的最优策略π*:S→R，首先定义vπ:S→R为每个状态s∈S遵循策略π*收到的累积折扣回报的期望，即：

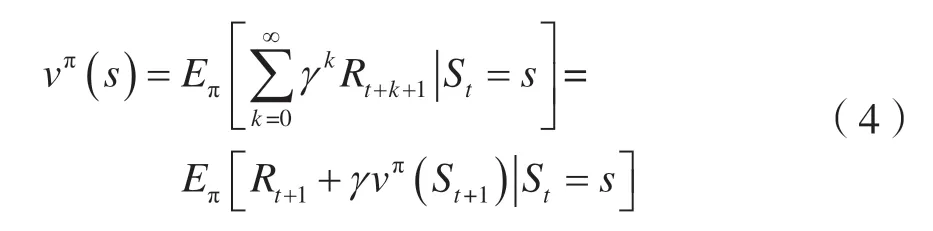
类似可以得到所有状态行为对的价值函数：

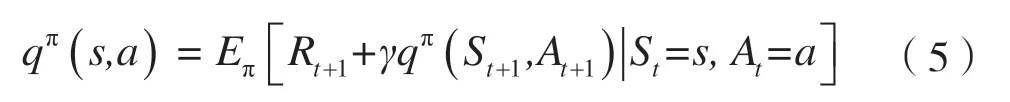
可以从所有策略产生的状态价值函数中，选取使状态s价值最大的函数，即最优状态价值函数：

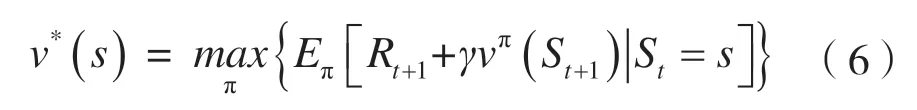
于是，可以得到每个状态的最优价值，最终获得最优策略π*。

针对v*(s)，一个状态的最优价值等于从该状态出发，采取的所有行为所产生的行为价值中的最大值，则最优状态价值函数可以表示为：

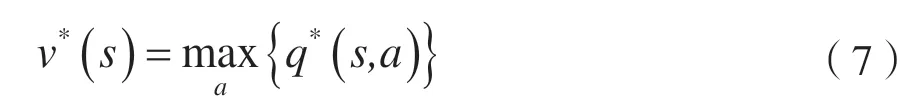
整个问题将简化为寻找行为价值函数qπ(s,a)的最优值Q*(s,a)。按照式（8）反复迭代，即可得到最优策略。

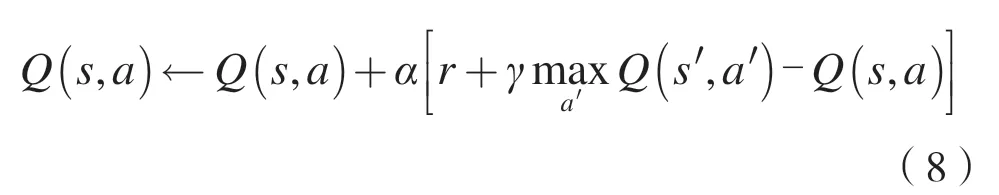
传统的Q学习算法在状态空间和行为空间较小的时候能够有效获得最优的策略。然而，在实际应用过程中，智能体的状态空间和行为空间往往都十分庞大，此时Q学习算法便很难取得理想效果。因此，将深度学习与Q学习算法相结合的深度强化学习网络（Deep Q-Network，DQN）算法可以很好地克服这一缺点。

强化学习的数据通常是非静态、非独立均匀分布，一个状态数据可能是持续流入的，而且下一个状态通常与前一个状态高度相关。因此，Q函数值的微小偏差都会影响整个策略。当使用非线性近似估计方法时，强化学习算法得到的回报并不稳定且Q函数不易收敛。对此，DQN采用经验回放的方法，将过去的训练数据以(st,at,rt,st+1)的形式存放在经验池中，每次随机提取一部分数据作为神经网络的输入进行训练[10]。通过使用经验回放，打破了原始数据之间的关联性，使训练数据变得更加独立均匀分布。

DQN采用两个结构相同但参数不同的神经网络，如图3所示。

图3 基于深度强化学习的DQN算法框架

一个Q网络为原始网络，根据输入的当前状态和动作计算原始网络Q值。另一个Q网络称为目标网络，通过计算可以得到目标Q值：

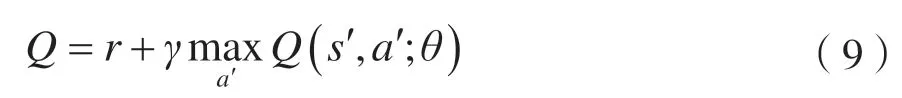
再通过梯度下降法最小化目标Q值和原始网络Q值的偏差，得到的最新权值参数用于更新原始网络，而目标网络使用的参数相对较落后。通过这种方式，目标Q值和原始网络Q值之间的相关性显著降低，算法变得更加稳定。

DQN方法能够处理大规模的系统，可以直接从历史经历中找到接近最优的策略。同时，深度强化学习可以通过与环境的实时交互获得最新的训练数据，神经网络也能获得更好的拟合性能。

针对本系统，考虑到发送节点和接收节点的位置会影响SINR，进而影响智能体制定决策。将每条通信链路所分配的信道、功率以及发送节点和接收节点所在坐标作为环境特征即S=(c,p,xs,ys,xr,yr)，并选取离当前时刻最近的T组环境特征作为状态空间即St=(St,St-1,…,St-T+1)，最终整个状态空间的矩阵大小为6×k×T。行为空间由分配的可用信道和功率组成。面对未知的动态环境和网络状态，数据传输过程中可能产生额外的能量消耗和传输延迟，导致能量效率下降。为了平衡当前最好的Q值和探索更好的Q值，DQN采用ε-贪婪策略随机选择行为，即使用1-ε的概率贪婪地选择具有最大行为价值的行为，使用ε的概率随机从所有可选行为中选取一种行为。ε-贪婪探索机制的目标是使得某一状态下所有可能的行为都有非零几率被选中执行，也就保证了持续的探索[2]。为了使算法可以收敛，ε会随着算法的迭代过程逐渐减小并趋于0。考虑到目标是实现能量效率的优化，将回报定义为能量效率，表示为：

如果当次决策的能量效率低于一定阈值，智能体将施加一定的惩罚，使回报值为负数。

3 仿真与分析

本节通过仿真结果实现复杂动态无线网络的信道和功率分配，提高能量效率，对实验场景和相关参数进行介绍，并对实验结果和性能作出分析。

为了证实DQN算法在复杂网络环境能否取得良好的效果，本文模拟多信道接入无线网络环境建立模型，随机选取30个节点组成15条通信链路，设置4个可选择信道，功率组合为2 mW、5 mW和9 mW。因此，动作空间的大小为12。本文构建的仿真模型和深度强化学习均由Python实现，并且基于TensorFlow、Gym和Keras设计和训练了DQN算法。本实验的网络参数和深度强化学习算法参数取值如表1和表2所示。训练所使用的神经网络为全连接神经网络，包含2个隐含层，每个隐含层分别拥有256和9个神经元。每个神经元使用的激活函数为修正线性单元（ReLU）。折扣因子的大小决定了算法对当前回报和未来回报的重视程度，折扣因子越小，算法越倾向于短期的高收益。由于本实验中需要连续做出一系列的动作，为了获得更加长期的高额回报，本文将折扣因子设置为0.9。

表1 无线网络参数取值

表2 DQN算法参数取值

基于上述动态无线网络的场景模拟，本实验对15条通信链路进行了200个回合的信道和功率分配。取每个回合的平均奖励值作为该回合的决策值，并将每回合的决策值与全部回合的最大决策值的比值作为性能指标。如图4所示，经过反复的迭代更新，算法的性能指标逐渐由负值上升为正值，且随着回合数的增加，逐渐收敛在0.1～0.4。由此可知，本算法对整个网络的信道、功率资源分配正逐步趋于合理，所带来的能量效率收益也得到大幅提高。如图5所示，随着算法的反复训练，将所有通信链路分配完成所需的迭代次数也逐渐收敛在一个稳定的范围内。

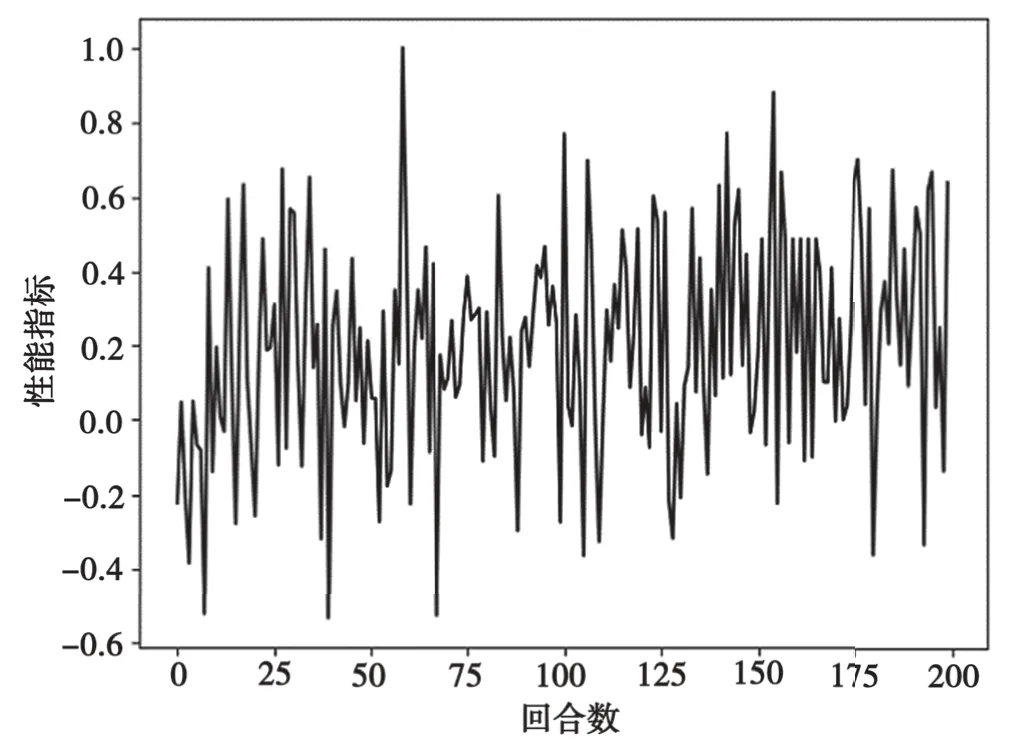
图4 每回合的算法性能指标

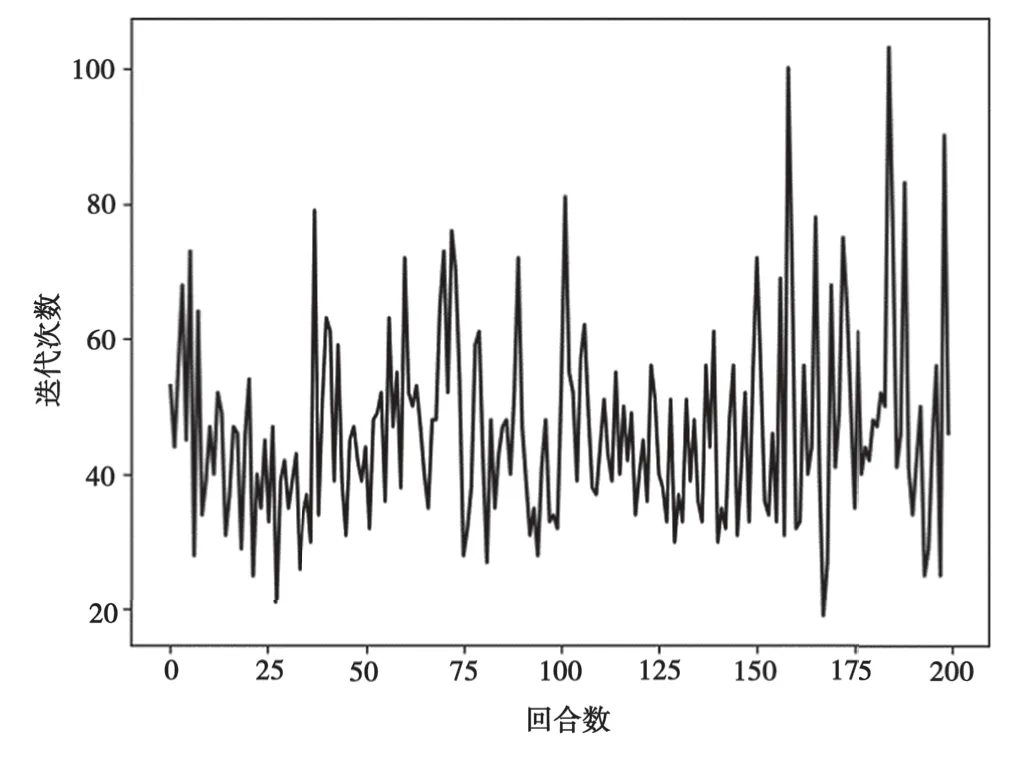
图5 每回合的迭代次数

综上所述，通过提出的复杂动态无线网络资源分配的算法，智能体能够动态分配可用信道和功率，不断学习过往的经历，最终得到接近最优的分配策略，提高整个网络的能量效率。

4 结语

为了解决复杂动态无线网络中资源分配的问题，满足所有通信链路分配的同时，尽可能提高网络全局的能量效率，本文提出了一种基于深度强化学习的信道和功率分配算法。通过结合深度学习理论构建误差函数，将能量效率作为奖惩值，进行反复训练更新神经网络权值参数。仿真结果表明，随着训练回合数的不断增加，提出的算法可以得到接近最优的资源分配策略，能够很好地优化系统能耗，有效解决复杂动态网络环境下的资源分配问题。