一种极坐标下基于高斯过程的扩展目标跟踪方法

郭云飞,任 昕

(杭州电子科技大学自动化学院,浙江杭州 310018)

1 引言

现代战争中复杂的目标环境,要求雷达不仅能快速完成对于目标的测定,而且能够对目标进行识别.高精度传感器不仅提供了目标的运动信息,还可以检测到来自同一目标的多个散射点信息,因此扩展目标领域的跟踪成为当前的研究热点,在现代战场监控、识别等军事领域和智能驾驶、无人机等民用领域有重要的应用前景[1–2].雷达接收的数据是基于极坐标系下的数据,当变换到直角坐标系进行处理时,其转换测量期望值在目标真实方位上存在偏差,且转换后测量误差协方差的计算需要依赖真实目标的距离和角度信息,在实际中无法完成[3–4].相反,直接利用基于极坐标系下的雷达数据进行滤波,避免了转换误差和估计误差,可以消除这部分精度的损失.

针对扩展目标跟踪问题,文献[5]提出了基于高斯过程的扩展目标跟踪方法,通过利用高斯过程对扩展目标的轮廓进行建模,但是非线性测量条件下不适用.文献[3]提出了无相关无偏转换测量(decorrelated unbiased converted measurement,DUCM)方法,并在与雷达测量相关的跟踪场景中评估了转换方法.文献[6–7]在文献[3]的基础上,测量中增加了多普勒信息的使用.在文献[8]和文献[9]中提出了一种基于随机矩阵(random matrices,RM)的椭圆扩展目标跟踪方法,该算法直接用椭圆对扩展目标进行逼近,简单有效.然而对于较复杂的非椭圆形扩展目标,无法体现目标的细节并达到形态估计的目的.在文献[10]中提出了一种基于随机超曲面模型扩展目标跟踪方法,结合中心轮廓距离提出了自适应轮廓的方法对突变的目标进行航迹和形状的估计.文献[11]提出了一种适合的测量模型来解决雷达的测量噪声并将其转换到笛卡尔坐标,通过使用X波段雷达获取的模拟数据和实际数据,结合随机矩阵理论对扩展目标进行跟踪.文献[12]提出了一种使用非线性测量的扩展目标随机矩阵方法,使用匹配线性化(matched linearization,ML)来线性化非线性测量,然后将线性化的测量结果合并到现有的随机矩阵算法中.文献[13]在去除杂波时,提出了一种在挑战性的真实数据集上使用点样本和聚类算法,通过基于间隔的方法来处理数据关联并减少数据关联过程中的计算复杂性,从而实现对杂波的去除.

针对雷达系统,杂波环境下的扩展目标跟踪问题,本文提出了一种极坐标下基于高斯过程的扩展目标跟踪(Gaussian process based extended target tracking for nonlinear measurement probability data association,GP–NM–PDA)方法,该方法对测量模型进行重新建模,并改变了相对应的测量噪声协方差以及互联概率,并通过仿真进行验证.

2 问题描述

2.1 运动模型

通常扩展目标状态由运动学状态和轮廓状态组成[14].扩展目标的运动学模型如下:

其中: Xk[(Xk)T表示k时刻扩展目标的状态;Fkdiag{Fk,表示k时刻扩展目标的状态转移矩阵;νk[(υk)T表示零均值的高斯白噪声,其对应的协方差Qkdiag{Qk,,并且和υk之间是相互独立的.因此,式(1)可以改写为

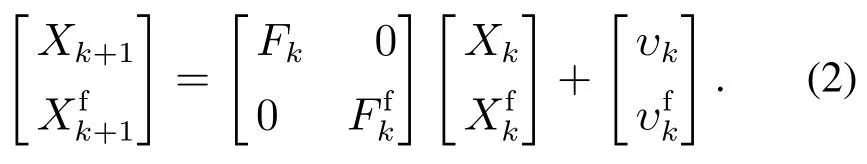
运动状态Xk描述扩展目标中心点的运动特征,[xkyk]T和分别为k时刻扩展目标中心点的位置向量和速度向量,ϕk和分别为k时刻扩展目标的航向角和航向角速度.

在扩展目标跟踪方法中,一般扩展目标的轮廓信息是未知的.随机矩阵模型通过正定矩阵,假设目标是一个简单的椭圆[8].而高斯过程模型可以利用每一时刻的当前测量信息,对于目标的径向函数进行更新,实时在线估计出扩展目标的轮廓.基于高斯过程模型,[fk(θ1)fk(θ2)··· fk(θNt)]T表示为扩展目标的轮廓状态,其轮廓半径函数fk(θ)可以表示为下列形式[15]:

其中: σr表示均值半径的标准差;σf表示轮廓半径函数协方差的标准差;参数l表示SE函数的尺度因子,为标量.

2.2 测量模型

假设Ck为k时刻传感器接收到Mk个位置测量,其中j表示k时刻传感器接收到的第j个位置测量.对于第j个位置测量得到下列测量模型,其中j取值范围为:1jMk,

假设在检测区域内,杂波密度服从均匀分布,杂波个数服从参数为λm的泊松分布,真实测量噪声为∼N(0,R),其对应的噪声协方差为R表示扩展目标中心点的位置;随机尺度因子∈[0,1]服从高斯分布,即表示局部坐标系下测量与目标中心点的夹角;∥·∥2表示Euclidean范数;全局坐标系下为测量与扩展目标中心点连线和水平方向的夹角.相对应在局部坐标系中(即以扩展目标为原点建立的直角坐标系)的角度.ϕk为扩展目标在k时刻的航向角,具体参见扩展目标在全局坐标系和局部坐标系下示意图1;测量具体表达式如下:

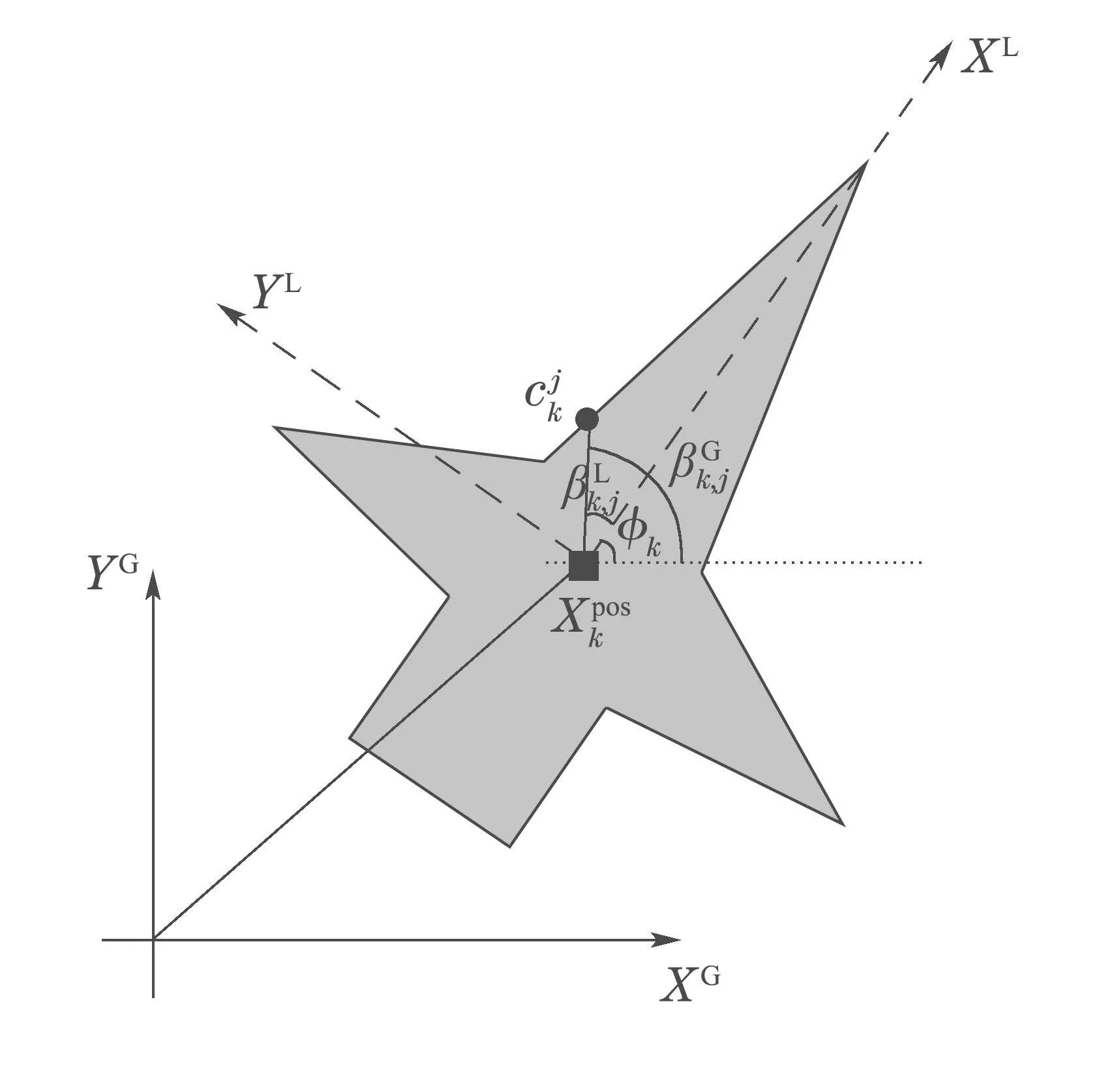
图1 扩展目标在全局坐标系和局部坐标系下的示意图Fig.1 Sketch map of the extended target in the global coordinate system and the local coordinate system

由于真实的扩展目标轮廓函数fk是未知且时变的.基于高斯过程模型,轮廓函数fk可由下列公式替代:

其中函数σ(θ,θ′)表达式见式(4).因此,结合式(5)−(6)和式(11),最终得到的测量模型见式(12).

引理1

证毕.

3 无偏测量转换

转换测量跟踪是一种在坐标系统中进行滤波的技术,需要将测量值非线性拟合.测量转换的目标是允许在笛卡尔坐标系中进行跟踪,这对于描述系统动力学是最自然的[3].但是在执行转换的测量时会出现两个潜在问题.首先是当测量变换在转换的测量的预期值中引入偏差时发生的转换偏差;第2种是发生估计偏差,因为转换的测量误差协方差的估计与测量噪声相关,导致偏置的卡尔曼增益[6].因此,为了克服转换偏差和估计偏差,应采用无偏测量转换,使用预测测量计算转换后的测量误差协方差.

其中σr和σθ分别表示测量距离噪声和角度噪声的标准差.

4 极坐标系下基于高斯过程的扩展目标跟踪方法

为了解决雷达系统,杂波环境下的扩展目标跟踪问题,本文提出了一种极坐标下基于高斯过程的扩展目标跟踪(GP–NM–PDA)方法,可以用于解决非线性测量下的扩展目标跟踪问题.在处理杂波时,文献[13]是直接通过基于密度的聚类方法,实现对杂波的去除,从而降低数据关联计算中的复杂性.而本文所提方法是通过建立扩展目标联合跟踪门,考虑落入跟踪波门内的有效量测,根据不同的相关情况,利用贝叶斯公式计算关联事件后验概率,然后将所有相关事件的条件估计与相应的事件后验概率相结合,最终得到融合后的状态估计和协方差估计.

GP–NM–PDA方法的基本框架与传统的PDA方法框架相似,该方法主要贡献是重新计算了测量模型中的雅克比矩阵,适用于雷达系统下的非线性测量数据.其算法流程图如图2所示.

图2 GP–NM–PDA算法框架图Fig.2 GP–NM–PDA algorithm framework diagram

步骤1扩展目标的预测状态和预测协方差.

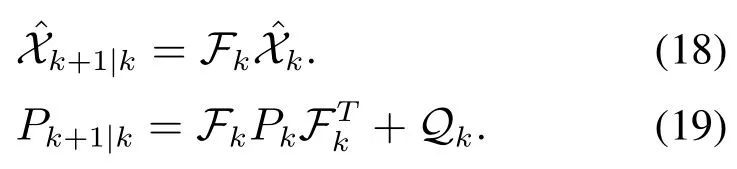
步骤2计算预测测量.

在扩展目标跟踪系统中,扩展目标轮廓上的散射点位置和个数都是不确定.第k+1时刻目标的测量预测需要结合当前有效测量[16]和目标状态即对于k+1时刻的第j个有效测量,预测测量的具体公式如下:

步骤3扩展目标联合跟踪门.

雷达传感器每一时刻接收到的测量中会有多个源自扩展目标的量测,以当前时刻的每一个预测测量为中心建立子跟踪门.如果第k+1时刻的第j个测量落入到该子跟踪门内,则认为该测量有效.将所有的子跟踪门求并集即可建立扩展目标跟踪门.子跟踪门的具体表达式如下:

其中: mk+1表示经过跟踪门筛选的测量个数;(1imk+1)表示k+1时刻每个有效测量的跟踪门.总跟踪门Ωk+1的体积Vk+1具体公式如下:

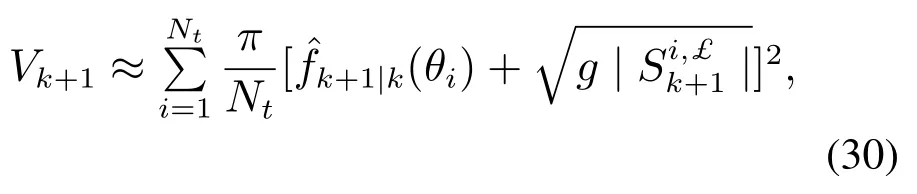
其中: Nt表示预测的扩展目标轮廓点的个数;(θi,表示预测的扩展目标轮廓点;由式(26)−(28)计算得出,其中将替换为θi.

步骤4关联事件.

如果在k+1时刻,跟踪门内有效测量个数为mk+1个,则所有的关联事件[14]定义为

其中: φ表示来自扩展目标的测量个数;nφ表示来自扩展目标的测量个数是φ时,关联事件的个数.

步骤5扩展目标状态估计更新.

基于扩展卡尔曼框架和扩展目标的状态一步预测,然后通过全概率公式,结合关联事件的条件概率和关联概率,最后得到修正后的状态估计和协方差估计.

步骤6扩展目标状态协方差更新.

扩展目标状态估计相对应的协方差为

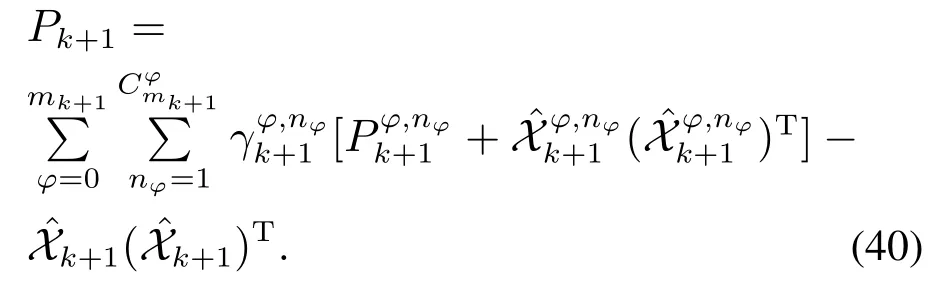
5 仿真分析

在本文的仿真中,假设该扩展目标以近似匀速直线运动,测试GP–NM–PDA方法在杂波环境中跟踪扩展目标的可靠性.为了证明所提方法的有效性,选择扩展目标质心位置均方根误差(root mean square error,RMSE)、轮廓位置RMSE、航向角RMSE等性能指标,将GP–NM–PDA方法与GP–EKF方法、随机矩阵方法进行对比分析.

5.1 性能指标

质心位置RMSE:设k时刻真实目标位置向量为[xkxyk]T,经M次蒙特卡洛仿真后,得到k时刻目标的位置向量估计为,则k时刻目标的质心位置均方根误差为

航向角RMSE:设k时刻真实目标的航向角为ϕk,经M次蒙特卡洛仿真后,得到k时刻目标的航向角估计,则k时刻目标的航向角RMSE Ξk为

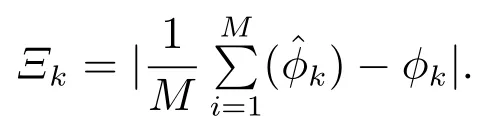
轮廓位置RMSE:设k时刻真实目标的轮廓函数为fk(βj),经M次蒙特卡洛仿真后,得到k时刻扩展目标的轮廓估计函数则k时刻目标的轮廓位置均方根误差为

5.2 仿真场景1:扩展目标轮廓固定不变

本次仿真采用100次蒙特卡洛运行并参考下列性能指标.所有方法在MATLAB上实现.

具体参数设置:已知的扩展目标状态信息

在GP–NM–PDA方法中,扩展目标的中心运动状态模型为CV模型,扩展目标状态转移矩阵Fk和质心运动过程噪声如下:

目标状态协方差初值P0diag{25 m2,1 m2/s2,25 m2,1 m2/s2,0.25 rad2,1×10−6rad2/s2}.假设扩展目标的轮廓状态在运动过程中保持不变,轮廓状态对应的过程噪声其中:,σθ测量噪声的距离标准差和角度标准差分别为σr0.65 m,σθ0.01 rad.

RM方法[13]参数设置:给定扩展目标的最初轮廓矩阵为

其中:Id为单位矩阵,空间维度d2,λ1/4用来刻画形态对方差的作用;自由度δ100;形态转移矩阵为

GP–EKF方法设置:首先将来自雷达传感器的测量数据转化到直角坐标系下进行线性化处理,然后基于GP–EKF方法对扩展目标进行跟踪,GP–EKF方法实现参考文献[5].

图3和图4分别为杂波密度λc2×10−4m−2、检测概率Pd0.9情况下,GP–NM–PDA方法和RM方法对扩展目标航迹跟踪和轮廓估计效果图.通过图3的放大效果图可以得出,GP–NM–PDA算法可以准确地刻画出复杂形状的目标轮廓和扩展目标的轨迹,跟踪效果明显.而RM方法只能得到扩展目标的大概区域.

图3 GP–NM–PDA方法目标跟踪效果图Fig.3 True and estimated trajectorise by GP–NM–PDA algorithm

图4 随机矩阵方法目标跟踪效果图Fig.4 True and estimated trajectorise by random matrix algorithm

由图5−7可以看出,在中心点位置估计RMSE方面,相比较GP–EKF方法,本文提出的GP–NM–PDA方法可以在初期就迅速收敛,在达到稳定状态后效果最优,GP–EKF在当前仿真环境下次之,RM方法对于目标中心位置的估计较差.

图5 扩展目标中心位置估计RMSEFig.5 RMSE of centroid position estimate of target

图6 扩展目标航向角估计Fig.6 RMSE of heading estimate of target

图7 扩展目标轮廓位置估计RMSEFig.7 RMSE of contour position estimate of target

在轮廓位置估计RMSE 方面,GP–NM–PDA 方法和GP–EKF 方法在对于扩展目标的轮廓估计方面相差很小,均稳定在5 m ∼6 m之间,这是由于两种方法对于扩展目标的轮廓估计都是基于高斯过程模型来进行估计;在航向角估计方面,相对GP–EKF方法,GP–NM–PDA方法优势最大,对于估计精度更准确,稳定后误差在0.1 rad ∼0.2 rad之间,接近克拉美罗下界,其具体计算公式参考文献[14].

在时间资源消耗方面,本文所提GP–NM–PDA方法与GP–EKF 方法和随机矩阵方法相比,时间消耗相差无几,本文所提方法并没有过多的增加运行时间.

接下来,在杂波密度λc2×10−4m−2,不同检测概率Pd0.7,Pd0.8和Pd0.9条件下,验证GP–NM–PDA方法的性能并进行分析.

由图8−10可以看出,扩展目标中心位置RMSE方面,检测概率Pd0.9条件下最终稳定在5.0 m左右.当检测概率Pd减小到5.5时,该方法跟踪精度误差达到15 m左右.在航向角RMSE方面,检测概率Pd0.9时,稳定在0.07 rad左右,对于目标的航向估计精度高,有利于对目标航行的准确把握,当检测概率小于或等于Pd0.7,航向角RMSE已经达到了0.57 rad左右,不具备参考价值.在目标轮廓位置RMSE方面,检测概率在大于等于0.6的条件下,误差精度保持在7 m以下,可以准确估计出目标的轮廓,有利于目标的识别.

图8 不同检测概率下扩展目标航向角估计Fig.8 RMSE of heading estimate with different Pd

图9 不同检测概率下扩展目标中心位置RMSEFig.9 RMSE of centroid estimate with different Pd

图10 不同检测概率下扩展目标轮廓位置RMSEFig.10 RMSE of contour estimate with different Pd

为了进一步分析3种方法在不同参数下对目标跟踪精度的影响,考虑其中两个参数:杂波密度λc和检测概率Pd.注意在分析其中一个参数时,其他参数保持不变.

表1为在不同检测概率和不同杂波下的本文所提GP–NM–PDA方法和GP–EKF方法以及随机矩阵方法在目标中心位置、航向角、轮廓位置RMSE的对比.

表1 不同杂波密度λc和不同检测概率Pd下的性能统计Table 1 Position estimation error of three algorithms against different parameters

由表1可以看出,随着检测概率Pd增大,GP–NM–PDA方法和GP–EKF方法对目标机舰的中心位置、航向角、轮廓位置估计误差均减小.随机矩阵方法对目标机舰的中心位置估计误差也逐渐降低.在相同的Pd条件下,本文所提GP–NM–PDA方法在估计扩展目标航向角方面优势最大,当Pd0.9时,性能达到最佳,误差仅为0.069 rad;GP–NM–PDA 方法和GP–EKF 方法在轮廓位置估计方面差距较小,在5 m ∼6 m之间.随着杂波密度λc增大,3种方法对目标机舰的中心位置、航向角、轮廓位置估计误差均增大.

5.3 仿真场景2:扩展目标轮廓时变

该场景模拟扩展目标在运动过程中,由于扩展目标和雷达接收站的视角变化引起的目标面积随时间的增加而减小.传感器采样周期为T1 s,总帧数为80 帧.杂波个数服从泊松分布,单位面积上杂波密度为λc1×10−4m−2.其余参数与场景1保持一致.

图11−12可以看出随着时间增加,扩展目标的面积由1040 m2减小到260 m2时,GP–NM–PDA的跟踪效果良好,依然可以估计出较为准确的目标轮廓信息,能够应对复杂的目标轮廓时变情况.

表2给出了在不同检测概率下的各性能的估计精度以及算法的运行时间.从表中可以得出,目标的中心位置RMSE保持在10 m以内,跟踪效果理想.

图11 扩展目标轮廓时变GP–NM–PDA跟踪效果Fig.11 True and estimated trajectorise by GP–NM–PDA algorithm when extended target contour time-varying

图12 扩展目标面积随时间变化柱状图Fig.12 Histogram of target area over time

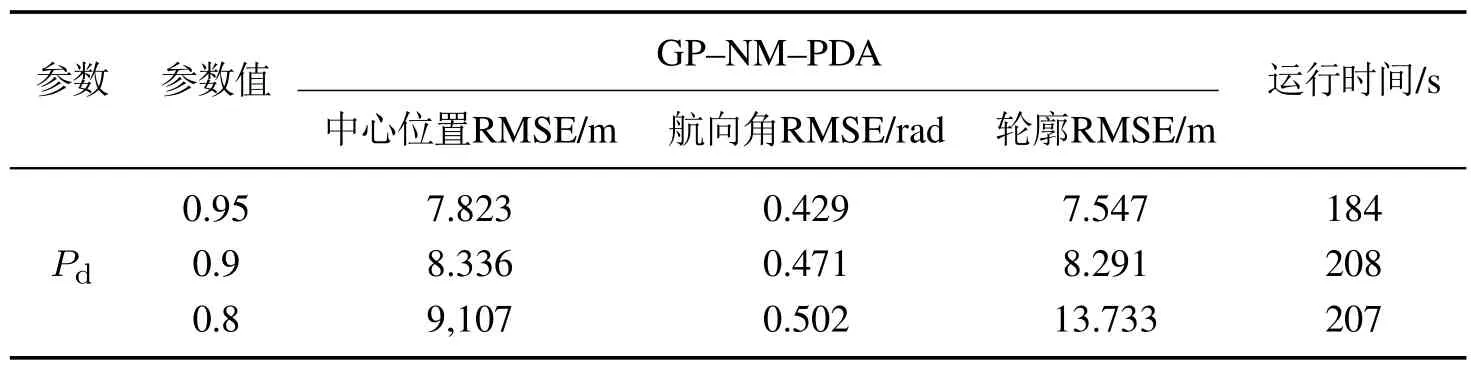
表2 不同检测概率Pd的性能统计Table 2 Performance of different detection probability

对比表1在目标轮廓不变时的GP–NM–PDA的性能估计,可以得出当目标轮廓时变,在相同检测概率下,主要影响的是扩展目标的航向角RMSE和轮廓位置RMSE.这是由于随着目标运动,距离接收站越来越远,接收站接收到来自目标表面的有效信息会越来越少,导致跟踪精度的降低.但是在检测概率Pd0.8时仍然可以将误差控制在10 m以内,体现出本文所提算法可以很好的应对扩展目标的轮廓时变.

6 结论

本文针对杂波环境、非线性测量条件(距离和角度)下的扩展目标跟踪问题,对于所提的GP–NM–PDA方法和GP–EKF方法以及RM方法进行了仿真验证.仿真结果表明GP–NM–PDA方法和GP–EKF 方法均可以有效的对扩展目标进行轮廓估计和跟踪,但是GP–NM–PDA方法具有更小的滤波误差和更快的收敛速度,能更加准确估计目标航向,对航迹的跟踪效果更好.这是因为GP–EKF方法在对测量变换过程中会引入转换偏差和估计偏差,从而跟踪精度降低.而GP–NM–PDA方法是直接利用雷达测量数据进行滤波跟踪,避免了转换偏差和估计偏差,同时结合了概率数据关联算法,利用贝叶斯公式计算事件后验概率,更新各扩展目标的状态.与GP–EKF方法相比,GP–NM–PDA方法没有过多的增加运行时间.

通过仿真可以得出,本文所提GP–NM–PDA方法在扩展目标轮廓以及航向角方面有效提高了跟踪性能,同时也验证了该方法可以很好适应目标轮廓大小时变的情况.